Is 72/96 Equivalent To 12/16
zacarellano
Sep 07, 2025 · 5 min read
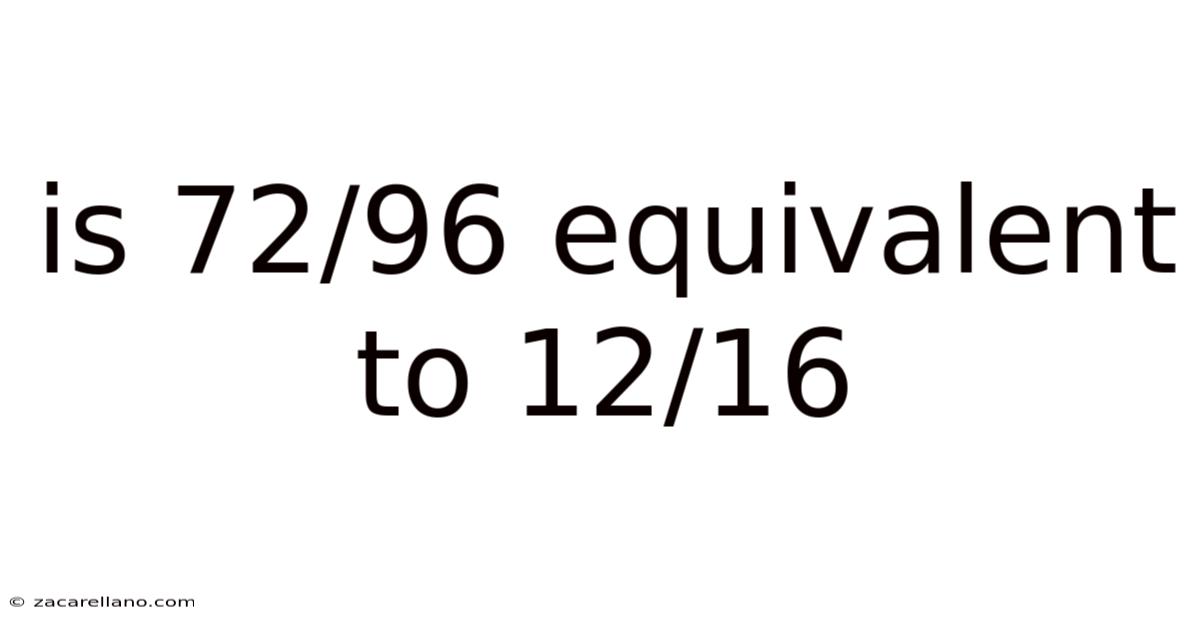
Table of Contents
Is 72/96 Equivalent to 12/16? A Deep Dive into Fraction Simplification and Equivalence
Are the fractions 72/96 and 12/16 equivalent? This seemingly simple question opens the door to a deeper understanding of fractions, their simplification, and the fundamental concept of equivalence. This article will not only answer this question definitively but also explore the underlying mathematical principles, providing a comprehensive guide suitable for students and anyone seeking to improve their understanding of fractions. We'll delve into various methods for simplifying fractions and explore why understanding equivalence is crucial in mathematics and beyond.
Introduction to Fractions and Equivalence
A fraction represents a part of a whole. It's written as a ratio of two integers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the whole is divided into four equal parts, and we are considering three of them.
Two fractions are considered equivalent if they represent the same proportion or value. This means that they occupy the same position on the number line. Even though they look different, they represent the same portion of the whole. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. All these fractions represent exactly half of a whole.
Method 1: Simplifying Fractions to Their Lowest Terms
The most straightforward way to determine if 72/96 and 12/16 are equivalent is by simplifying each fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's start with 12/16:
- Find the GCD of 12 and 16: The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 16 are 1, 2, 4, 8, and 16. The greatest common factor is 4.
- Divide both the numerator and denominator by the GCD: 12 ÷ 4 = 3 and 16 ÷ 4 = 4.
- Simplified fraction: 12/16 simplifies to 3/4.
Now, let's simplify 72/96:
-
Find the GCD of 72 and 96: This might require a little more work. We can use the Euclidean algorithm or list the factors, but a quicker method is to find the prime factorization of each number.
- 72 = 2³ x 3²
- 96 = 2⁵ x 3
The GCD is found by taking the lowest power of each common prime factor: 2³ x 3 = 24.
-
Divide both the numerator and denominator by the GCD: 72 ÷ 24 = 3 and 96 ÷ 24 = 4.
-
Simplified fraction: 72/96 simplifies to 3/4.
Since both 72/96 and 12/16 simplify to 3/4, they are equivalent.
Method 2: Cross-Multiplication
Another way to check for equivalence is through cross-multiplication. If two fractions a/b and c/d are equivalent, then their cross-products are equal: a x d = b x c.
Let's apply this to 72/96 and 12/16:
- Cross-multiply: 72 x 16 = 1152 and 96 x 12 = 1152.
- Comparison: Since both cross-products are equal (1152 = 1152), the fractions 72/96 and 12/16 are equivalent.
This method is particularly useful when dealing with larger numbers where finding the GCD might be more challenging.
Method 3: Visual Representation
While not as mathematically rigorous as the previous methods, visualizing fractions can enhance understanding. Imagine a pizza cut into 16 slices. 12/16 represents 12 slices out of 16. Now, imagine another pizza cut into 96 slices. 72/96 represents 72 slices out of 96. If you simplify the number of slices in each scenario (by dividing by their respective GCDs), you'll find that both scenarios represent the same proportion of the pizza – three-quarters.
The Importance of Fraction Simplification and Equivalence
Understanding fraction simplification and equivalence is crucial for several reasons:
- Simplifying calculations: Working with simplified fractions makes calculations easier and less prone to errors. Imagine adding 72/96 and another fraction – it’s much simpler to work with the equivalent 3/4.
- Comparing fractions: Determining which fraction is larger or smaller is much easier when they are simplified to their lowest terms.
- Understanding proportions: Equivalence is fundamental to understanding proportions and ratios, which are vital in many fields, including cooking, engineering, and finance.
- Solving equations: Many algebraic equations involve fractions, and simplifying and finding equivalent fractions is essential for solving them.
Frequently Asked Questions (FAQs)
Q: Are there other fractions equivalent to 72/96 and 12/16?
A: Yes, infinitely many. Any fraction obtained by multiplying both the numerator and denominator of 3/4 by the same non-zero integer will be equivalent. For example, 6/8, 9/12, 15/20, etc., are all equivalent to 3/4.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It's like reducing a complex situation to its simplest form.
Q: Can I use a calculator to simplify fractions?
A: Yes, many calculators have a function to simplify fractions. However, understanding the underlying mathematical principles is crucial for developing a strong foundation in mathematics.
Q: What if the cross-products aren't equal?
A: If the cross-products aren't equal, the fractions are not equivalent.
Q: Is there a limit to how many equivalent fractions exist for a given fraction?
A: No, there are infinitely many equivalent fractions for any given fraction, except for 0/1 (or any fraction equivalent to it).
Conclusion
We have definitively shown that 72/96 and 12/16 are equivalent fractions, both simplifying to 3/4. We explored three different methods to demonstrate this equivalence: simplifying to lowest terms, cross-multiplication, and visual representation. This seemingly simple problem has provided a springboard for exploring the fundamental concepts of fractions, simplification, and equivalence, highlighting their importance in mathematics and various applications in the real world. Mastering these concepts provides a solid foundation for more advanced mathematical studies. Remember, the key is not just to get the right answer but also to understand the underlying reasoning and principles involved. This deeper understanding will serve you well in your mathematical journey.
Latest Posts
Latest Posts
-
Line Integral Of Scalar Function
Sep 08, 2025
-
Science Topics For 7th Graders
Sep 08, 2025
-
George Washington By Jean Antoine Houdon
Sep 08, 2025
-
Money Word Problems 2nd Grade
Sep 08, 2025
-
What Is The Text About
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Is 72/96 Equivalent To 12/16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.