Is -8 Greater Than -9
zacarellano
Sep 20, 2025 · 5 min read
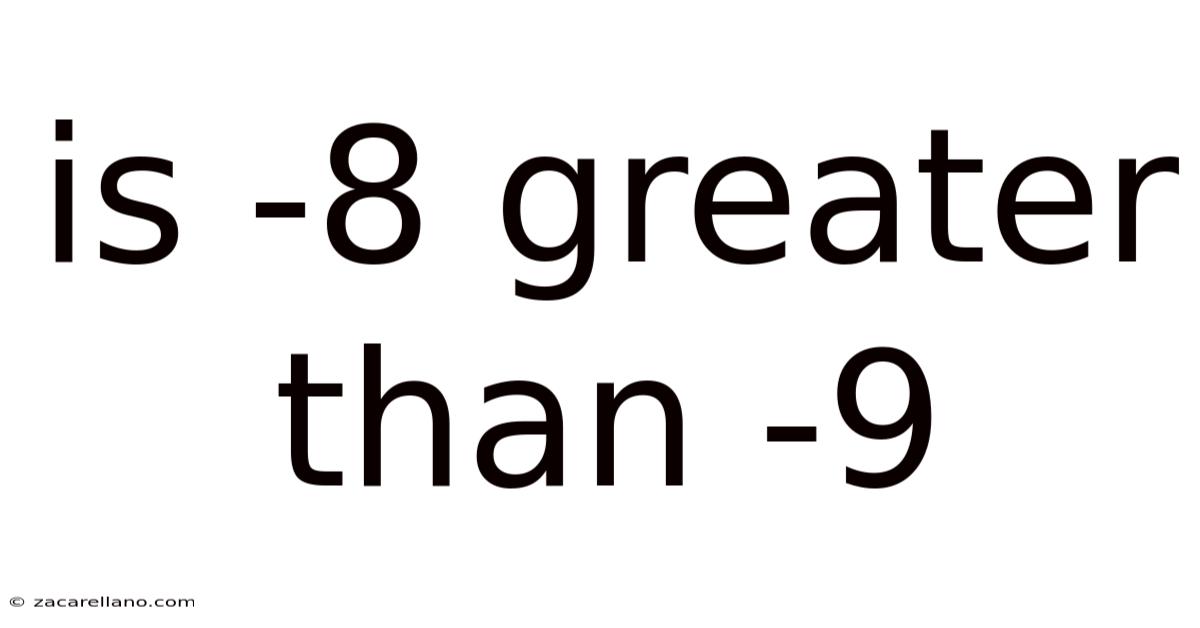
Table of Contents
Is -8 Greater Than -9? Understanding Negative Numbers
This seemingly simple question, "Is -8 greater than -9?", often trips up people unfamiliar with the intricacies of negative numbers. While intuitively, we might think smaller numbers are always less, the introduction of negative numbers requires a shift in our understanding of numerical magnitude. This article will thoroughly explain why -8 is indeed greater than -9, exploring the concept of negative numbers, their representation on the number line, and their practical applications. We’ll also delve into some common misconceptions and provide clear examples to solidify your understanding.
Understanding the Number Line
The number line is a fundamental tool for visualizing numbers and their relationships. It extends infinitely in both directions, with zero at its center. Positive numbers are located to the right of zero, and negative numbers are located to the left. The further a number is from zero in either direction, the greater its magnitude (or absolute value).
Imagine the number line:
... -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 ...
Notice how -8 is positioned to the right of -9. On the number line, numbers increase as you move to the right. Therefore, any number to the right of another number is considered greater. This directly explains why -8 is greater than -9.
Why the Confusion?
The confusion often arises from our ingrained understanding of positive numbers. With positive numbers, a larger numerical value always represents a larger quantity. However, negative numbers represent debts or deficits. Thinking in terms of debt helps illustrate the concept.
Imagine you owe someone $9 (-$9) and your friend owes $8 (-$8). Who owes less? Your friend. Owing less is equivalent to having more, in the context of debt. Therefore, -$8 is a better financial position than -$9, meaning -8 is greater.
Comparing Negative Numbers: A Step-by-Step Approach
To compare any two negative numbers:
- Ignore the negative signs: Consider only the absolute values (the numbers without the negative sign).
- Compare the absolute values: The number with the smaller absolute value is greater.
- Reintroduce the negative signs: The number with the smaller absolute value retains its negative sign and represents the greater value.
Let's apply this to our example:
- Absolute Values: The absolute value of -8 is 8, and the absolute value of -9 is 9.
- Comparison: 8 is less than 9.
- Conclusion: Therefore, -8 is greater than -9.
Real-World Applications
Understanding negative numbers and their comparisons is crucial in various real-world scenarios:
- Temperature: -8°C is warmer than -9°C. A higher negative temperature indicates a less severe cold.
- Altitude: An altitude of -8 meters (8 meters below sea level) is higher than an altitude of -9 meters (9 meters below sea level).
- Finance: A bank account balance of -$8 is better than a balance of -$9. It represents a smaller debt.
- Scientific Measurements: In many scientific fields, negative numbers represent measurements below a zero point (e.g., negative pressure, negative charge). The comparison of these negative values follows the same principles.
Misconceptions and Clarifications
Some common misconceptions surrounding negative numbers include:
- Larger Number is Always Greater: This is true only for positive numbers. With negative numbers, the smaller numerical value is greater.
- Negative Numbers are "Smaller than Nothing": Negative numbers are less than zero, but they still have a magnitude and can be compared relative to each other.
- Ignoring the Context: The meaning of negative numbers is dependent on the context. In temperature, a higher negative value means a warmer temperature, but in debt, it signifies a larger debt.
Visualizing with the Number Line: More Examples
Let's compare some more pairs of negative numbers using the number line:
- -5 vs. -2: -2 is to the right of -5, so -2 > -5.
- -10 vs. -1: -1 is to the right of -10, so -1 > -10.
- -15 vs. -20: -15 is to the right of -20, so -15 > -20.
In each case, the number closer to zero (on the right) is the greater number.
Mathematical Operations with Negative Numbers
The rules for adding, subtracting, multiplying, and dividing negative numbers are essential for a complete understanding. While not directly related to the core question, grasping these rules solidifies the comprehension of the number line and the concept of negative magnitudes.
- Addition: Adding a negative number is the same as subtracting its positive counterpart (e.g., 5 + (-3) = 5 - 3 = 2).
- Subtraction: Subtracting a negative number is the same as adding its positive counterpart (e.g., 5 - (-3) = 5 + 3 = 8).
- Multiplication: Multiplying two negative numbers results in a positive number (e.g., (-3) * (-2) = 6).
- Division: Dividing two negative numbers results in a positive number (e.g., (-6) / (-2) = 3).
Frequently Asked Questions (FAQ)
Q1: Can you explain why -8 is greater than -9 in a simple way?
A1: Think of a thermometer. -8 degrees is warmer (higher) than -9 degrees. On the number line, -8 is to the right of -9, meaning it's greater.
Q2: Is it always true that a smaller negative number is greater?
A2: Yes, this is a fundamental rule when comparing negative numbers. The number closer to zero (on the right of the number line) is always greater.
Q3: What happens if I compare a negative number with a positive number?
A3: Any positive number will always be greater than any negative number. For example, 1 > -100.
Q4: How can I avoid making mistakes when comparing negative numbers?
A4: Visualize the numbers on a number line. Remember that the number further to the right is always greater. Use the three-step approach outlined earlier to systematically compare negative numbers.
Conclusion
In conclusion, -8 is indeed greater than -9. This understanding stems from a clear grasp of the number line and the implications of negative numbers. While counterintuitive at first, mastering the comparison of negative numbers is crucial for understanding various mathematical and real-world concepts. By applying the methods and principles explained in this article, you can confidently compare negative numbers and avoid common misconceptions. Remember to visualize the number line, think in terms of debt or deficits, and use the step-by-step approach to solidify your understanding. The seemingly simple question of "Is -8 greater than -9?" opens the door to a deeper comprehension of the fascinating world of numbers.
Latest Posts
Latest Posts
-
Is Denominator Top Or Bottom
Sep 20, 2025
-
Grammar Subject Verb Agreement Exercises
Sep 20, 2025
-
Fractional Vs Simple Distillation Graph
Sep 20, 2025
-
Individuals In A Data Set
Sep 20, 2025
-
Growth Mindset Activities For Adults
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is -8 Greater Than -9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.