Is -sqrt2 Greater Than 0
zacarellano
Sep 17, 2025 · 5 min read
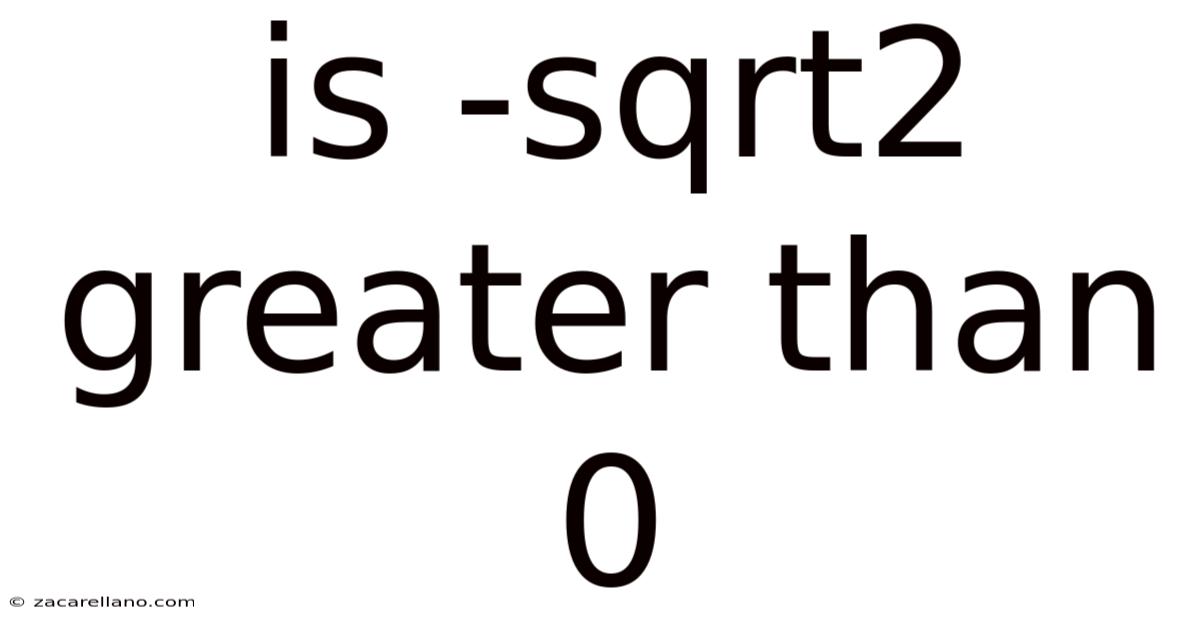
Table of Contents
Is -√2 Greater Than 0? Understanding Negative Square Roots and Number Lines
This article explores the seemingly simple question: Is -√2 greater than 0? While the answer might seem immediately obvious to some, a deeper understanding requires exploring the concepts of square roots, negative numbers, and their representation on the number line. This comprehensive guide will not only answer the question definitively but also provide a solid foundation in these crucial mathematical concepts. We'll delve into the properties of real numbers, visualizing them graphically, and addressing common misconceptions.
Understanding Square Roots and the Concept of √2
The symbol √ (radical) denotes the principal square root. The principal square root of a non-negative number x is the non-negative number y such that y² = x. In simpler terms, it's the positive number that, when multiplied by itself, gives you the original number.
For example:
- √9 = 3 because 3 * 3 = 9
- √16 = 4 because 4 * 4 = 16
- √0 = 0 because 0 * 0 = 0
Now, let's consider √2. This is an irrational number, meaning it cannot be expressed as a simple fraction. Its approximate value is 1.414. Crucially, √2 is positive because the principal square root is always non-negative.
Introducing Negative Numbers and Their Position on the Number Line
The number line is a visual representation of numbers, extending infinitely in both positive and negative directions. Zero sits at the center. Numbers to the right of zero are positive, and numbers to the left are negative. The further a number is from zero, the larger its magnitude (absolute value).
- Positive numbers: These are greater than zero.
- Negative numbers: These are less than zero.
- Zero: This is neither positive nor negative. It is the neutral point on the number line.
Addressing the Core Question: Is -√2 Greater Than 0?
Now, we can directly address the main question. We know that √2 ≈ 1.414. Therefore, -√2 ≈ -1.414.
Since -1.414 is located to the left of 0 on the number line, it is less than 0.
Therefore, the answer is definitively no, -√2 is not greater than 0. In fact, -√2 is less than 0.
Visualizing on the Number Line
Imagine a number line:
-3 -2 -1 0 1 2 3
|
-√2 (approximately -1.414)
As you can see, -√2 is clearly positioned to the left of 0.
Understanding the Importance of the Negative Sign
The negative sign (-) preceding √2 fundamentally changes its value. It indicates the opposite of the principal square root of 2. It's not simply a matter of ignoring the negative; it dictates the position and value relative to zero.
Expanding on Irrational Numbers and Their Properties
As mentioned earlier, √2 is an irrational number. Irrational numbers are non-repeating, non-terminating decimals. They cannot be expressed as a fraction of two integers. Despite their seemingly complex nature, irrational numbers are essential components of the real number system. Understanding them is crucial for grasping more advanced mathematical concepts.
Comparing Real Numbers: Order and Magnitude
The real number system encompasses all rational and irrational numbers. These numbers can be ordered on the number line, reflecting their relative magnitudes. A number further to the right is always greater than a number further to the left.
Comparing numbers involves understanding their position relative to zero and to each other. Positive numbers are always greater than zero, and negative numbers are always less than zero. Comparing two negative numbers requires considering their distance from zero – the number closer to zero is larger.
Applications of Square Roots and Negative Numbers
Understanding square roots and negative numbers isn't just an academic exercise; these concepts have broad applications across various fields:
- Physics: Calculations involving vectors, displacement, and velocity often incorporate negative numbers and square roots.
- Engineering: Structural design, electrical circuits, and many other engineering disciplines require a solid grasp of these mathematical fundamentals.
- Computer Science: Algorithms, data structures, and simulations frequently employ square roots and negative numbers.
- Finance: Calculations involving compound interest, present value, and future value commonly utilize these concepts.
Frequently Asked Questions (FAQ)
Q1: What is the difference between √2 and -√2?
A1: √2 represents the principal square root of 2, which is a positive value (approximately 1.414). -√2 represents the negative of this value, which is a negative number (approximately -1.414).
Q2: Can we have a negative square root of a positive number?
A2: While the principal square root of a positive number is always positive, every positive number has two square roots: a positive one and a negative one. For example, the square roots of 9 are +3 and -3. However, only the positive one is considered the principal square root.
Q3: How do I represent -√2 on a calculator?
A3: Most calculators will have a square root function (√). To get -√2, calculate √2 first, then multiply the result by -1.
Q4: What about the square root of a negative number?
A4: The square root of a negative number (e.g., √-9) is not a real number. These are called imaginary numbers, which are a different type of number system extending beyond the real numbers. They are represented using the imaginary unit i, where i² = -1.
Q5: Is there any practical situation where -√2 is relevant?
A5: Yes, there are many. For example, in physics, you might encounter -√2 when calculating a vector component in a direction opposite to a reference axis. The negative sign simply indicates direction.
Conclusion: A Solid Grasp of Fundamentals
This detailed exploration demonstrates that -√2 is not greater than 0. Understanding this seemingly simple question requires a solid grasp of square roots, negative numbers, and their representation on the number line. This extends to a broader understanding of real numbers, their properties, and their extensive applications in various fields. By reinforcing these fundamental mathematical concepts, we can build a strong foundation for more advanced mathematical endeavors. Remember, the seemingly simple questions often lead to a deeper appreciation of the underlying principles.
Latest Posts
Latest Posts
-
1 8 X 1 8
Sep 17, 2025
-
Science Questions For 6th Graders
Sep 17, 2025
-
Parallel Lines Never Intersect Because
Sep 17, 2025
-
What Is Probability In Biology
Sep 17, 2025
-
Abstract Words And Concrete Words
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is -sqrt2 Greater Than 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.