Is X 0 No Solution
zacarellano
Sep 08, 2025 · 6 min read
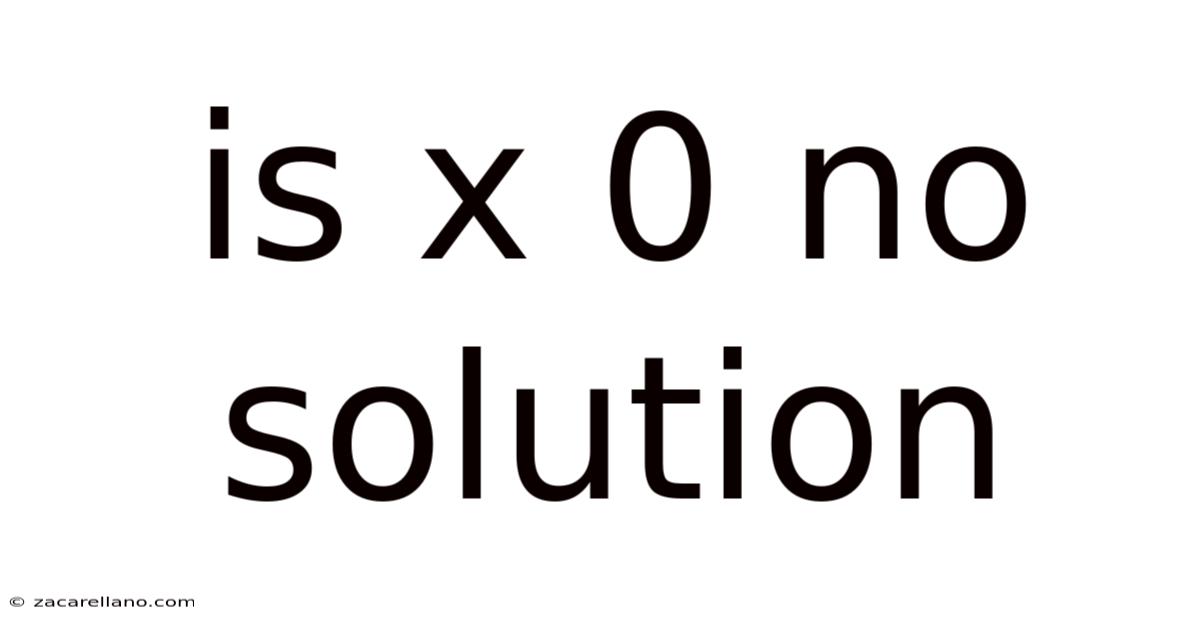
Table of Contents
Is x * 0 = 0 No Solution? Understanding the Multiplicative Property of Zero
The question, "Is x * 0 = 0 no solution?" might seem trivial at first glance. After all, anything multiplied by zero equals zero, right? However, a deeper understanding of the multiplicative property of zero reveals a more nuanced answer, and this seemingly simple equation touches upon fundamental concepts in algebra and mathematics. This article will explore this property, explain why there isn't a "no solution" scenario in this case, and delve into related mathematical concepts to provide a comprehensive understanding.
Understanding the Multiplicative Property of Zero
The multiplicative property of zero is a fundamental axiom in mathematics. It states that for any real number x, the product of x and 0 is always 0. This can be expressed mathematically as:
x * 0 = 0
This property holds true for all real numbers, including positive numbers, negative numbers, zero itself, rational numbers, irrational numbers, and even complex numbers. It's a cornerstone of arithmetic and algebra, influencing numerous mathematical operations and theorems.
The reason why this property holds true lies in the very definition of multiplication. Multiplication can be viewed as repeated addition. For example, 3 * 4 means adding 3 four times: 3 + 3 + 3 + 3 = 12. If we apply this logic to x * 0, it means adding x zero times. Adding nothing results in nothing – zero.
Why x * 0 = 0 Doesn't Have "No Solution"
The statement "x * 0 = 0 has no solution" is incorrect. In fact, it has infinitely many solutions. Any real number substituted for 'x' will satisfy the equation. This is because regardless of the value of x, multiplying it by zero always results in zero.
Let's consider some examples:
- If x = 5: 5 * 0 = 0 (True)
- If x = -2: -2 * 0 = 0 (True)
- If x = 0: 0 * 0 = 0 (True)
- If x = π: π * 0 = 0 (True)
These examples demonstrate that the equation x * 0 = 0 is true for any value of x. Therefore, the solution set is the entire set of real numbers. This is a significant difference from equations that have a single solution or no solution at all. For instance, an equation like x + 2 = 5 has only one solution (x = 3), while an equation like x = x + 1 has no solution because no number can be equal to itself plus one.
Contrasting with Division by Zero
The multiplicative property of zero is often contrasted with the concept of division by zero, which is undefined. While multiplying by zero always results in zero, dividing by zero is a mathematical impossibility. This is because division is the inverse operation of multiplication. If we try to solve the equation x / 0 = y, there's no number 'x' that can satisfy this equation for any value of 'y' because there's no number you can multiply by zero to obtain a non-zero result.
This undefined nature of division by zero is fundamentally different from the infinitely many solutions of x * 0 = 0. The former represents an operation that is not defined within the real number system, while the latter has a well-defined solution set.
The Zero Product Property and its Implications
The multiplicative property of zero is closely related to the zero product property, a crucial concept in solving polynomial equations. The zero product property states that if the product of two or more factors is zero, then at least one of the factors must be zero. This is expressed as:
If ab = 0, then a = 0 or b = 0 (or both)
This property is widely used in solving quadratic equations and higher-degree polynomial equations. For instance, to solve the equation (x - 2)(x + 3) = 0, we can apply the zero product property:
- x - 2 = 0 => x = 2
- x + 3 = 0 => x = -3
Therefore, the solutions to the equation are x = 2 and x = -3. The zero product property relies heavily on the multiplicative property of zero.
Applications in Different Mathematical Fields
The multiplicative property of zero is not confined to basic arithmetic and algebra. Its influence extends to various branches of mathematics, including:
- Calculus: The concept of limits and derivatives often involve situations where quantities approach zero. Understanding the multiplicative property of zero is critical in evaluating such limits.
- Linear Algebra: In matrix operations, multiplying a matrix by a zero matrix always results in a zero matrix. This property plays a crucial role in various linear algebra theorems and applications.
- Abstract Algebra: The multiplicative property of zero is a fundamental axiom in various algebraic structures, such as rings and fields, which generalize the concept of numbers and their operations.
Addressing Common Misconceptions
Several misconceptions often surround the multiplicative property of zero. Let's clarify some of them:
-
Misconception: x * 0 = 0 means that 'x' is undefined.
-
Correction: x * 0 = 0 means that 'x' can be any real number.
-
Misconception: Since anything multiplied by zero is zero, the equation is meaningless.
-
Correction: While it's true that the result is always zero, the equation is meaningful because it illustrates a fundamental mathematical property and is used extensively in solving other equations.
-
Misconception: There's some special value of 'x' that would make x * 0 different from zero.
-
Correction: No such value exists. The property is universally true for all real numbers.
Frequently Asked Questions (FAQ)
Q: Is there any exception to the rule x * 0 = 0?
A: No, there are no exceptions within the standard real number system. This is a fundamental axiom.
Q: How does the multiplicative property of zero relate to the concept of infinity?
A: While not directly related, the concept of limits approaching zero and infinity are often studied together in calculus. Understanding the multiplicative property of zero is essential for correctly interpreting limits involving zero.
Q: Can this property be proven?
A: The multiplicative property of zero is usually considered an axiom – a fundamental assumption upon which other mathematical statements are based. It cannot be proven from more basic principles, but rather serves as a foundation for building the system of arithmetic and algebra.
Q: Why is division by zero undefined, but multiplication by zero is defined?
A: Division by zero is undefined because there is no number that, when multiplied by zero, results in a non-zero number. Multiplication by zero, on the other hand, always results in zero, which is a well-defined outcome.
Conclusion
The equation x * 0 = 0 does not represent a "no solution" scenario; instead, it has infinitely many solutions. This fundamental property, known as the multiplicative property of zero, is a cornerstone of arithmetic and algebra. Its implications extend far beyond basic calculations, playing a crucial role in various branches of mathematics. Understanding this seemingly simple property provides a foundation for grasping more complex mathematical concepts and solving more challenging problems. By understanding the distinction between multiplication and division by zero, and appreciating the significance of the zero product property, we gain a deeper appreciation for the elegant structure and consistency of mathematics.
Latest Posts
Latest Posts
-
Shapes Of Distributions In Statistics
Sep 09, 2025
-
What Is A Sine Ratio
Sep 09, 2025
-
Saint Matthew And The Angel
Sep 09, 2025
-
Enzyme Used To Digest Dna
Sep 09, 2025
-
Cadena Alimenticia De Los Animales
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Is X 0 No Solution . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.