L.c.m Of 3 And 6
zacarellano
Sep 11, 2025 · 6 min read
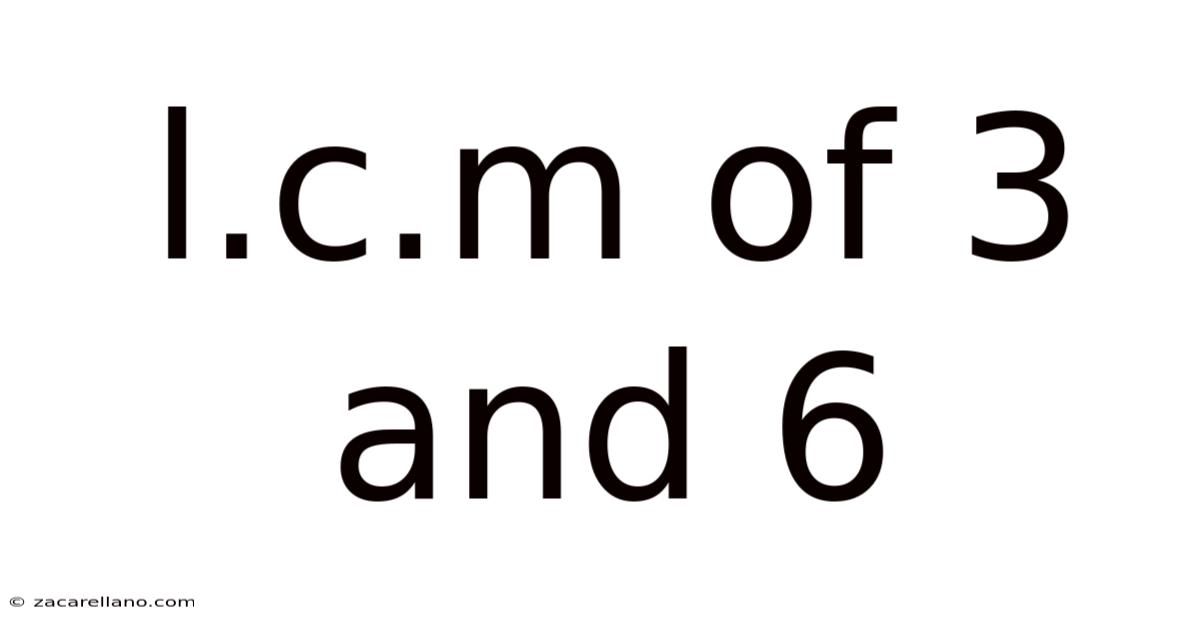
Table of Contents
Unveiling the LCM: A Deep Dive into the Least Common Multiple of 3 and 6
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 3 and 6. However, understanding the underlying principles of LCMs is crucial for grasping more advanced mathematical concepts in algebra, number theory, and even calculus. This article will not only show you how to calculate the LCM of 3 and 6 but will also delve into the theoretical foundations, explore different methods, and provide practical applications to solidify your understanding.
Introduction: What is a Least Common Multiple?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers in the set as factors. Understanding LCMs is essential for various mathematical operations, including adding and subtracting fractions with unlike denominators, solving problems involving cyclical events, and simplifying algebraic expressions.
Methods for Finding the LCM of 3 and 6
There are several ways to determine the LCM of 3 and 6. Let's explore the most common methods:
1. Listing Multiples:
This is the most straightforward method, especially for smaller numbers. We simply list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 6: 6, 12, 18, 24, 30...
The smallest number that appears in both lists is 6. Therefore, the LCM of 3 and 6 is 6.
2. Prime Factorization Method:
This method is particularly useful when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 3: 3 = 3¹
- Prime factorization of 6: 6 = 2¹ × 3¹
The prime factors present are 2 and 3. We take the highest power of each prime factor: 2¹ and 3¹. Multiplying these together gives us 2¹ × 3¹ = 6. Therefore, the LCM of 3 and 6 is 6.
3. Greatest Common Divisor (GCD) Method:
The LCM and GCD (greatest common divisor) of two numbers are related through a simple formula:
LCM(a, b) × GCD(a, b) = a × b
First, we find the GCD of 3 and 6. The GCD is the largest number that divides both 3 and 6 without leaving a remainder. In this case, the GCD(3, 6) = 3.
Now, we can use the formula:
LCM(3, 6) × GCD(3, 6) = 3 × 6 LCM(3, 6) × 3 = 18 LCM(3, 6) = 18 / 3 LCM(3, 6) = 6
This method proves again that the LCM of 3 and 6 is 6.
A Deeper Look at the Mathematics Behind LCM
The concept of LCM is deeply rooted in number theory. Understanding the prime factorization method reveals its fundamental connection to the structure of numbers. Every positive integer greater than 1 can be uniquely expressed as a product of prime numbers. This is known as the Fundamental Theorem of Arithmetic.
When we find the LCM using prime factorization, we are essentially building the smallest number that contains all the prime factors of both numbers, with each prime factor appearing at its highest power. This ensures that the resulting number is divisible by both original numbers. This principle extends to finding the LCM of more than two numbers as well.
For example, let's find the LCM of 12, 18, and 30.
- 12 = 2² × 3¹
- 18 = 2¹ × 3²
- 30 = 2¹ × 3¹ × 5¹
The prime factors are 2, 3, and 5. Taking the highest powers of each, we get 2², 3², and 5¹. Multiplying these gives us 2² × 3² × 5¹ = 4 × 9 × 5 = 180. Therefore, the LCM(12, 18, 30) = 180.
Applications of LCM in Real-World Scenarios
The concept of LCM has practical applications in various real-world situations:
-
Scheduling: Imagine you have two events that occur cyclically. One event happens every 3 days, and another happens every 6 days. The LCM will tell you when both events will occur on the same day. In this case, LCM(3, 6) = 6, so both events will coincide every 6 days.
-
Fraction Operations: Adding or subtracting fractions requires a common denominator, which is the LCM of the denominators. For instance, to add 1/3 and 1/6, we find the LCM of 3 and 6, which is 6. Then, we rewrite the fractions with a denominator of 6 before adding them: (2/6) + (1/6) = 3/6 = 1/2.
-
Gear Ratios: In mechanical engineering, gear ratios utilize the concept of LCM to determine the optimal gear arrangement for a specific speed or torque requirement. The LCM helps in calculating the least number of rotations needed for synchronization between different gears.
-
Music Theory: In music, the LCM is used to determine the least common multiple of note durations, crucial for understanding rhythmic patterns and compositions. For example, in a piece with a repeating 3-note pattern and a 6-note pattern, they will align every 6 notes (LCM(3,6) = 6).
Frequently Asked Questions (FAQs)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers without leaving a remainder. They are inversely related; as the GCD increases, the LCM decreases, and vice versa.
Q: How do I find the LCM of more than two numbers?
A: You can extend the methods discussed earlier to find the LCM of more than two numbers. The prime factorization method is particularly efficient for this. Find the prime factorization of each number, then take the highest power of each prime factor present across all the numbers. Multiply these highest powers together to obtain the LCM.
Q: What if the numbers have no common factors other than 1?
A: If the numbers are relatively prime (meaning their GCD is 1), their LCM is simply the product of the numbers. For example, the LCM of 3 and 5 is 15 (3 x 5 = 15).
Q: Can the LCM be smaller than the largest number in a set?
A: Yes, as demonstrated with the LCM of 3 and 6, where the LCM (6) is equal to the largest number in the set. This happens when the larger number is a multiple of the smaller number.
Q: Are there any online calculators or tools to find the LCM?
A: Yes, many online calculators are available that can efficiently compute the LCM of any set of numbers. However, understanding the underlying principles is far more valuable than relying solely on calculators.
Conclusion: Mastering the LCM
Understanding the least common multiple is a fundamental skill in mathematics with widespread applications. While finding the LCM of 3 and 6 is a relatively straightforward task, grasping the underlying concepts of prime factorization and the relationship between LCM and GCD provides a powerful foundation for tackling more complex mathematical problems. By mastering these concepts, you unlock the ability to solve problems in diverse fields, from scheduling and fraction operations to music theory and engineering. The journey to mastering LCM isn't just about memorizing formulas; it's about understanding the inherent mathematical structure that governs numbers and their relationships.
Latest Posts
Latest Posts
-
Surface Area Of Cereal Box
Sep 11, 2025
-
What Is A Divergence Test
Sep 11, 2025
-
Acid Base Reaction Organic Chemistry
Sep 11, 2025
-
What Is A Sequence Number
Sep 11, 2025
-
3 4 Lbs To Oz
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about L.c.m Of 3 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.