Lcm For 10 And 15
zacarellano
Sep 09, 2025 · 6 min read
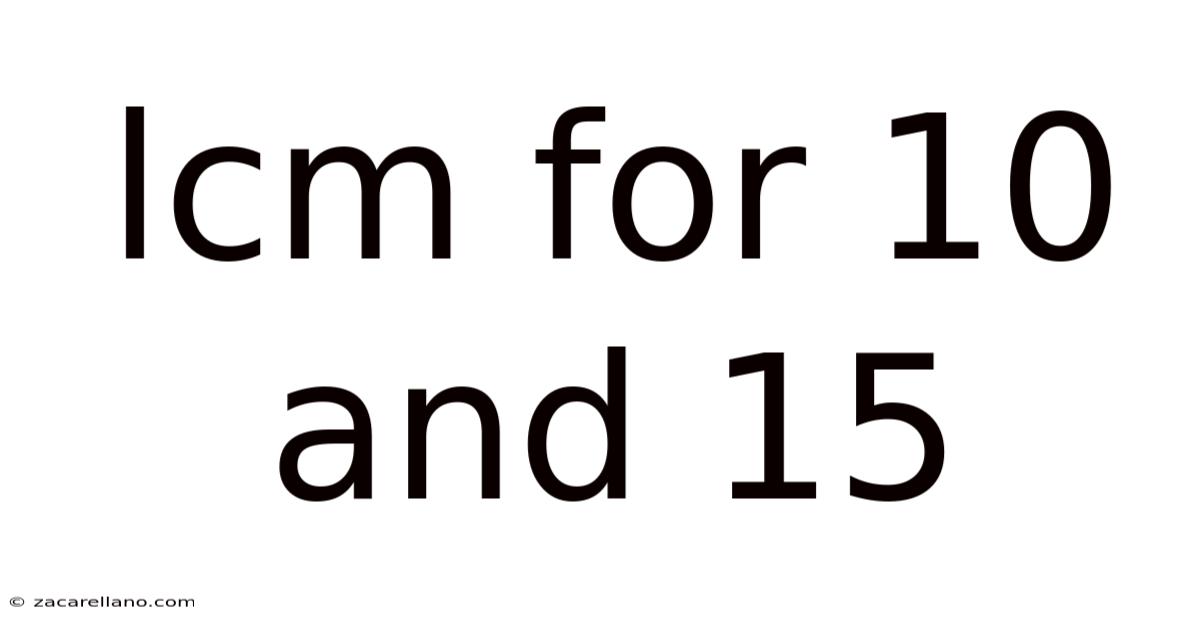
Table of Contents
Finding the Least Common Multiple (LCM) of 10 and 15: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 10 and 15, might seem like a simple arithmetic task. However, understanding the underlying concepts and various methods for calculating the LCM is crucial for mastering fundamental mathematics and its applications in various fields. This article will delve into the intricacies of finding the LCM of 10 and 15, explaining multiple approaches, their underlying logic, and providing a broader perspective on the significance of LCMs in mathematics. We'll cover everything from basic definitions to advanced techniques, making sure you fully grasp this important concept.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 10 and 15, let's establish a firm understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as its factors. This concept is fundamental in various mathematical operations, from simplifying fractions to solving problems related to cycles and patterns.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method to find the LCM of 10 and 15 is by listing their multiples until a common multiple is found. Let's do this:
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105...
Notice that 30 and 60 appear in both lists. However, 30 is the smallest number that is a multiple of both 10 and 15. Therefore, the LCM of 10 and 15 is 30. This method is straightforward for smaller numbers, but it becomes less efficient when dealing with larger numbers.
Method 2: Prime Factorization
This method offers a more systematic and efficient approach, especially when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Let's find the prime factorization of 10 and 15:
- 10 = 2 × 5
- 15 = 3 × 5
Now, we identify the prime factors present in both numbers: 2, 3, and 5. We take the highest power of each prime factor:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
To find the LCM, we multiply these highest powers together:
LCM(10, 15) = 2 × 3 × 5 = 30
This method is more efficient because it doesn't require listing out numerous multiples. It's particularly useful for larger numbers where the listing method becomes cumbersome.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This relationship provides another method for finding the LCM.
First, we need to find the GCD of 10 and 15. We can use the Euclidean algorithm for this:
- Divide the larger number (15) by the smaller number (10): 15 ÷ 10 = 1 with a remainder of 5.
- Replace the larger number with the smaller number (10) and the smaller number with the remainder (5): 10 ÷ 5 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 5.
Now, we can use the relationship between LCM and GCD:
LCM(a, b) = (a × b) / GCD(a, b)
Plugging in the values for 10 and 15:
LCM(10, 15) = (10 × 15) / 5 = 150 / 5 = 30
This method is efficient and relies on a well-established algorithm for finding the GCD.
The Significance of LCM in Real-World Applications
Understanding and calculating LCMs isn't just an academic exercise. It has significant practical applications in various fields:
- Scheduling: Imagine two buses leaving a station at different intervals. The LCM helps determine when both buses will depart at the same time again.
- Fraction Operations: Finding the LCM of denominators is essential for adding or subtracting fractions.
- Music Theory: LCM is used in music theory to calculate the least common denominator of musical rhythms, allowing for seamless transitions between rhythmic patterns.
- Engineering: In engineering and manufacturing, LCM calculations are used to synchronize moving parts or cycles in machines.
- Construction: LCM helps to align structures and components in construction projects, ensuring accurate and efficient construction.
Further Exploration: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider all the prime factors of all the numbers and take the highest power of each. For the GCD method, you can iteratively find the LCM of pairs of numbers.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The least common multiple (LCM) is the smallest number that is a multiple of all given numbers. The greatest common divisor (GCD) is the largest number that divides all given numbers without leaving a remainder. They are inversely related; as the GCD increases, the LCM decreases.
Q: Can the LCM of two numbers be one of the numbers?
A: Yes. If one number is a multiple of the other, the LCM will be the larger number. For example, the LCM of 6 and 12 is 12.
Q: Why is the prime factorization method considered efficient?
A: The prime factorization method is efficient because it directly addresses the fundamental building blocks of the numbers (prime factors). It avoids the need to list out many multiples, which becomes computationally expensive for larger numbers.
Q: Is there a single best method for finding the LCM?
A: The best method depends on the numbers involved. For small numbers, listing multiples is sufficient. For larger numbers, prime factorization or the GCD method are more efficient and less prone to errors.
Conclusion
Finding the least common multiple of 10 and 15, as demonstrated, is a fundamental mathematical skill with widespread applications. While the simple listing method works for smaller numbers, the prime factorization and GCD methods offer more efficient and robust approaches, especially when dealing with larger numbers or multiple numbers simultaneously. Understanding these methods and their underlying principles is crucial for a solid foundation in mathematics and for solving real-world problems that involve cyclical patterns, fractional calculations, and synchronized events. The ability to efficiently calculate LCMs demonstrates not only computational proficiency but also a deeper grasp of fundamental mathematical relationships. Remember, practice makes perfect, so try applying these methods to different number combinations to strengthen your understanding and develop your mathematical skills.
Latest Posts
Latest Posts
-
Para Que Sirve La Clorofila
Sep 09, 2025
-
Picture Of Cell Membrane Labeled
Sep 09, 2025
-
Ap Physics Unit 2 Review
Sep 09, 2025
-
Trigonometry Of Right Triangles Worksheet
Sep 09, 2025
-
Ap Bio Unit 2 Frq
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 10 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.