Lcm For 14 And 21
zacarellano
Sep 09, 2025 · 6 min read
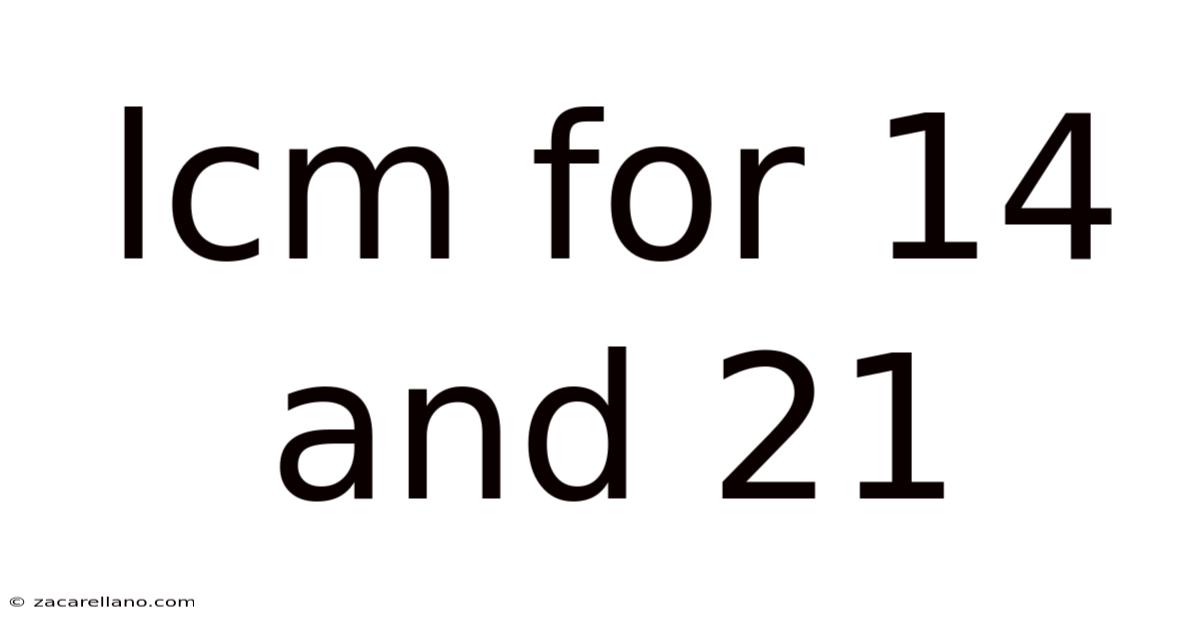
Table of Contents
Finding the Least Common Multiple (LCM) of 14 and 21: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving real-world problems involving cycles or repeating events. This comprehensive guide will delve into the different methods of calculating the LCM of 14 and 21, explaining the underlying principles and providing a deeper understanding of this important mathematical operation. We'll explore various approaches, ensuring you grasp the concept thoroughly and can apply it to other number pairs. This will include a detailed explanation of the prime factorization method, the listing method, and the use of the greatest common divisor (GCD). We'll also tackle some frequently asked questions (FAQs) to further solidify your understanding.
Understanding Least Common Multiple (LCM)
Before we jump into finding the LCM of 14 and 21, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers in the set as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
Method 1: Prime Factorization
The prime factorization method is a powerful and efficient way to find the LCM of any two numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to 14 and 21:
- Prime factorization of 14: 14 = 2 x 7
- Prime factorization of 21: 21 = 3 x 7
Now, we identify the prime factors present in either number. In this case, we have 2, 3, and 7. To find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together:
LCM(14, 21) = 2¹ x 3¹ x 7¹ = 2 x 3 x 7 = 42
Therefore, the least common multiple of 14 and 21 is 42. This means that 42 is the smallest positive integer divisible by both 14 and 21.
Method 2: Listing Multiples
This method is more straightforward but can become less efficient with larger numbers. It involves listing the multiples of each number until you find the smallest multiple common to both.
- Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126...
- Multiples of 21: 21, 42, 63, 84, 105, 126...
By comparing the lists, we can see that the smallest multiple common to both 14 and 21 is 42. Therefore, the LCM(14, 21) = 42. While this method works well for smaller numbers, it becomes cumbersome and time-consuming for larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are intimately related. There's a useful formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
where:
- a and b are the two numbers
- |a x b| represents the absolute value of the product of a and b
- GCD(a, b) is the greatest common divisor of a and b
First, we need to find the GCD of 14 and 21. We can use the Euclidean algorithm for this:
- Divide the larger number (21) by the smaller number (14): 21 ÷ 14 = 1 with a remainder of 7.
- Replace the larger number with the smaller number (14) and the smaller number with the remainder (7): 14 ÷ 7 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 7.
Now, we can use the formula:
LCM(14, 21) = (14 x 21) / 7 = 294 / 7 = 42
This method provides another efficient way to calculate the LCM, especially when dealing with larger numbers where listing multiples becomes impractical.
Visual Representation: Venn Diagram
A Venn diagram can help visualize the relationship between the prime factors and the LCM. Let's represent the prime factorization of 14 (2 x 7) and 21 (3 x 7) in a Venn diagram:
- The overlapping section (7) represents the GCD (7).
- The non-overlapping sections (2 and 3) represent the unique prime factors.
- The LCM is the product of all factors in the diagram: 2 x 3 x 7 = 42
This visual approach can provide a clearer understanding of the relationship between the prime factors, GCD, and LCM.
Real-World Applications of LCM
Understanding LCM has various practical applications:
- Scheduling: Imagine two buses arrive at a stop every 14 minutes and 21 minutes respectively. The LCM (42 minutes) tells us when both buses will arrive at the stop simultaneously again.
- Fraction Simplification: When adding or subtracting fractions, finding the LCM of the denominators is crucial for creating a common denominator.
- Cycling Problems: Problems involving repetitive cycles, like gears in a machine or repeating patterns, often require calculating LCM to determine when events coincide.
- Project Management: In project management, LCM can be used to synchronize tasks with different durations.
Frequently Asked Questions (FAQs)
Q1: What is the difference between LCM and GCD?
A1: The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. The GCD (Greatest Common Divisor) is the largest number that divides both numbers without leaving a remainder.
Q2: Can the LCM of two numbers be smaller than one of the numbers?
A2: No, the LCM will always be greater than or equal to the larger of the two numbers.
Q3: What if the two numbers are the same?
A3: If the two numbers are the same, then the LCM is simply the number itself. For example, LCM(14, 14) = 14.
Q4: Is there a formula to calculate the LCM directly without using prime factorization or the GCD?
A4: While there isn't a single direct formula that avoids factorization or GCD completely, iterative methods exist, though they're generally less efficient than the methods discussed above.
Q5: How can I find the LCM of more than two numbers?
A5: You can extend the prime factorization method to find the LCM of multiple numbers. Find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to obtain the LCM. For instance, to find the LCM of 14, 21, and 7: The prime factorizations are 2 x 7, 3 x 7, and 7. The LCM is 2 x 3 x 7 = 42.
Conclusion
Finding the LCM of 14 and 21, whether through prime factorization, listing multiples, or using the GCD, consistently yields the result of 42. Understanding the different methods allows you to choose the most efficient approach depending on the numbers involved. Mastering the concept of LCM opens doors to solving a wide range of mathematical problems and understanding real-world phenomena involving cycles and repetitions. Remember, the key is to break down the numbers into their prime factors, identify the common and unique factors, and then multiply them accordingly to arrive at the least common multiple. By understanding these principles, you'll be well-equipped to tackle more complex LCM problems in the future.
Latest Posts
Latest Posts
-
Irrational Vs Rational Numbers Worksheet
Sep 09, 2025
-
1st Horseman Of The Apocalypse
Sep 09, 2025
-
Para Que Sirve La Clorofila
Sep 09, 2025
-
Picture Of Cell Membrane Labeled
Sep 09, 2025
-
Ap Physics Unit 2 Review
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 14 And 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.