Lcm For 7 And 4
zacarellano
Sep 10, 2025 · 6 min read
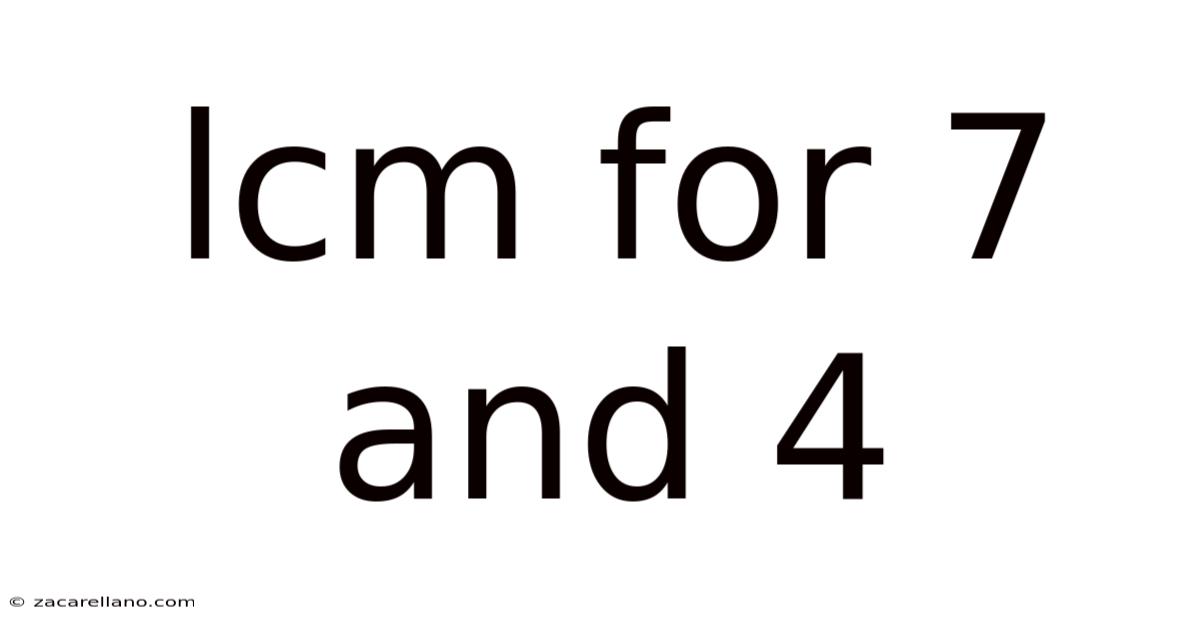
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 4: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in arithmetic and number theory, with applications ranging from simple fraction addition to complex scheduling problems. This article provides a comprehensive guide to understanding and calculating the LCM of 7 and 4, exploring various methods and delving into the underlying mathematical principles. We'll move beyond a simple answer and explore the "why" behind the calculations, making this concept clear and accessible to everyone, from elementary school students to those brushing up on their math skills.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding LCM is crucial for various mathematical operations, especially when working with fractions and simplifying expressions. This article focuses on finding the LCM of 7 and 4, illustrating different methods that can be applied to find the LCM of any two (or more) numbers.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers like 7 and 4. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, ...
By comparing the lists, we can see that the smallest number appearing in both lists is 28. Therefore, the LCM of 7 and 4 is 28.
This method works well for small numbers, but it becomes less efficient when dealing with larger numbers. Imagine trying to find the LCM of 7 and 47 using this method – you'd end up writing out a very long list of multiples! This highlights the need for more efficient methods for larger numbers.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the LCM of any set of integers, regardless of their size. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Find the prime factorization of each number:
- 7 is a prime number, so its prime factorization is simply 7.
- 4 can be factored as 2 x 2, or 2².
-
Identify the highest power of each prime factor:
- The prime factors involved are 2 and 7.
- The highest power of 2 is 2² = 4.
- The highest power of 7 is 7¹ = 7.
-
Multiply the highest powers together:
- LCM(7, 4) = 2² x 7 = 4 x 7 = 28
This method is significantly more efficient than listing multiples, especially for larger numbers. It provides a systematic approach that guarantees finding the LCM.
Method 3: Using the Formula (LCM and GCD Relationship)
The least common multiple (LCM) and the greatest common divisor (GCD) of two numbers are intimately related. There's a formula that elegantly connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
where:
aandbare the two integers.GCD(a, b)is the greatest common divisor ofaandb.|a x b|represents the absolute value of the product of a and b (which is always positive).
Let's apply this to 7 and 4:
-
Find the GCD of 7 and 4:
The GCD of 7 and 4 is 1, as they share no common factors other than 1. This can be found using the Euclidean algorithm or by inspection (since 7 is a prime number and not a factor of 4).
-
Apply the formula:
LCM(7, 4) = (7 x 4) / GCD(7, 4) = 28 / 1 = 28
This method demonstrates the elegant relationship between LCM and GCD. Finding the GCD can sometimes be easier than directly finding the LCM, especially for larger numbers, making this a very efficient approach.
A Deeper Dive: Understanding Prime Factorization
The prime factorization method's success relies on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This uniqueness is crucial because it ensures that we'll always arrive at the same LCM, regardless of the order in which we perform the factorization.
Let's illustrate this with a more complex example, finding the LCM of 12 and 18:
-
Prime Factorization:
- 12 = 2² x 3
- 18 = 2 x 3²
-
Highest Powers:
- Highest power of 2: 2² = 4
- Highest power of 3: 3² = 9
-
Multiply:
- LCM(12, 18) = 2² x 3² = 4 x 9 = 36
This example demonstrates how the prime factorization method handles multiple prime factors and their powers, providing a robust and generalizable solution.
Applications of LCM:
The LCM has numerous applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators.
-
Scheduling Problems: LCM is crucial for solving problems involving cyclical events. For example, determining when two machines operating at different cycles will coincide requires finding the LCM of their cycle times.
-
Modular Arithmetic: LCM plays a role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Music Theory: Finding common multiples is relevant in music theory when dealing with rhythms and harmonic progressions.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors (other than 1)?
- A: If the GCD of two numbers is 1 (meaning they are relatively prime), their LCM is simply their product. As seen with 7 and 4, their LCM is 7 x 4 = 28.
-
Q: Can I use this method for more than two numbers?
- A: Yes! The prime factorization method extends seamlessly to finding the LCM of more than two numbers. You simply find the prime factorization of each number, identify the highest power of each prime factor present, and multiply those highest powers together.
-
Q: Is there a way to find the LCM quickly for very large numbers?
- A: While the prime factorization method is efficient for many scenarios, for extremely large numbers, more sophisticated algorithms are employed. These algorithms often leverage the relationship between LCM and GCD and use techniques like the Euclidean algorithm for efficient GCD calculation.
Conclusion:
Finding the least common multiple (LCM) is a fundamental skill with practical applications across numerous domains. This article has explored various methods for calculating the LCM, focusing on the LCM of 7 and 4 but providing techniques applicable to any pair (or set) of integers. Mastering the prime factorization method provides a powerful tool for efficiently finding the LCM of even very large numbers. Understanding the underlying mathematical principles allows for a deeper appreciation of this essential concept in number theory. The ability to confidently calculate LCM empowers you to tackle a broader range of mathematical problems, highlighting the importance of mastering this seemingly simple yet powerful tool.
Latest Posts
Latest Posts
-
Are Negative Numbers Real Numbers
Sep 10, 2025
-
Sncc Civil Rights Movement Fashion
Sep 10, 2025
-
Niagara By Frederic Edwin Church
Sep 10, 2025
-
Does Mass Affect Kinetic Energy
Sep 10, 2025
-
Gcf Of 20 And 28
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 7 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.