Lcm Of 12 And 7
zacarellano
Sep 14, 2025 · 6 min read
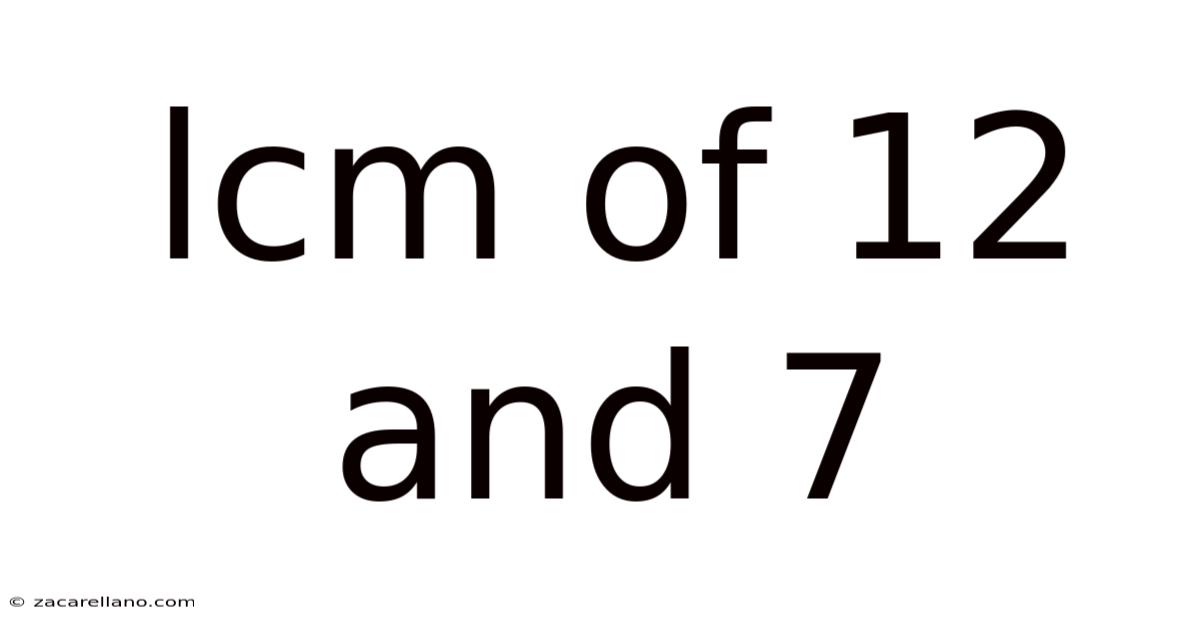
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 7: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts is crucial for grasping more advanced mathematical principles. This comprehensive guide will delve into the calculation of the LCM of 12 and 7, exploring different methods and providing a deeper understanding of this fundamental concept in number theory. We'll cover various approaches, from listing multiples to using prime factorization, ensuring you gain a solid grasp of the topic.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 12 and 7, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
Think of it like finding the smallest common ground for a set of numbers. For instance, if you're planning a party and need to buy enough snacks for 12 people and 7 people, you wouldn't want to buy separate quantities for each group. Finding the LCM helps determine the minimum number of snacks to buy so that both groups receive an equal and whole share.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until you find the smallest common multiple.
Let's start with 12:
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168...
Now, let's list the multiples of 7:
Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98...
By comparing both lists, we can see that the smallest number that appears in both lists is 84. Therefore, the LCM of 12 and 7 is 84.
This method works well for smaller numbers, but it can become quite tedious and time-consuming for larger numbers.
Method 2: Prime Factorization
Prime factorization is a more efficient and systematic method for finding the LCM, especially when dealing with larger numbers. This method involves breaking down each number into its prime factors – the prime numbers that multiply together to give the original number.
Prime factorization of 12:
12 = 2 x 2 x 3 = 2² x 3
Prime factorization of 7:
7 is a prime number, so its prime factorization is simply 7.
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations of both numbers and multiply them together.
- The prime factors present are 2, 3, and 7.
- The highest power of 2 is 2² = 4.
- The highest power of 3 is 3¹ = 3.
- The highest power of 7 is 7¹ = 7.
Therefore, the LCM of 12 and 7 is: 2² x 3 x 7 = 4 x 3 x 7 = 84.
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
Another approach to finding the LCM involves utilizing the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. There's a useful relationship between the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
Finding the GCD of 12 and 7:
Since 7 is a prime number and 12 is not divisible by 7, the GCD of 12 and 7 is 1.
Now, we can use the formula:
LCM(12, 7) x GCD(12, 7) = 12 x 7
LCM(12, 7) x 1 = 84
Therefore, the LCM of 12 and 7 is 84.
This method relies on first finding the GCD, which can be done using various techniques such as the Euclidean algorithm (especially efficient for larger numbers). However, for smaller numbers like 12 and 7, the GCD is easily identifiable by inspection.
Why is the LCM important?
Understanding LCMs is fundamental to various mathematical applications and real-world scenarios:
- Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling: Determining when events will occur simultaneously (e.g., buses arriving at the same stop) involves using LCMs.
- Modular Arithmetic: LCMs are used in modular arithmetic, which has applications in cryptography and computer science.
- Geometry: LCMs can be used in geometry problems involving finding common multiples of lengths or angles.
- Music Theory: LCMs help determine the least common denominator for musical rhythms and time signatures.
Frequently Asked Questions (FAQ)
Q: Is the LCM always greater than the two numbers?
A: Not always. If one number is a multiple of the other, the LCM will be the larger of the two numbers. For example, the LCM of 6 and 12 is 12.
Q: Can the LCM of two numbers be the same as one of the numbers?
A: Yes, as explained above. This happens when one number is a multiple of the other.
Q: How do I find the LCM of more than two numbers?
A: You can extend the prime factorization method to include more numbers. Find the prime factorization of each number, take the highest power of each prime factor, and multiply them together. You can also use the iterative approach, finding the LCM of two numbers, then finding the LCM of that result and the next number, and so on.
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers without leaving a remainder. They are inversely related; a higher GCD implies a lower LCM, and vice-versa.
Q: Are there any online calculators to find the LCM?
A: Yes, many online calculators are readily available to compute the LCM of any set of numbers quickly. However, understanding the underlying methods remains crucial for applying the concept effectively in different contexts.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with far-reaching applications. While the simple listing method works for small numbers, the prime factorization method provides a more efficient and scalable approach, especially when dealing with larger numbers or multiple numbers. Understanding the relationship between LCM and GCD further expands your mathematical toolkit. Mastering these methods will not only improve your arithmetic skills but also lay a solid foundation for more advanced mathematical concepts. Remember, practice is key to mastering this fundamental skill! Try finding the LCM of different number pairs to solidify your understanding and build your confidence.
Latest Posts
Latest Posts
-
Exponents And Powers Class 7
Sep 14, 2025
-
What Is 3 8 Inch
Sep 14, 2025
-
Apwh Unit 7 Practice Test
Sep 14, 2025
-
Define Addition Property Of Equality
Sep 14, 2025
-
Inputs And Outputs Of Fermentation
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.