Lcm Of 2 3 5
zacarellano
Sep 15, 2025 · 6 min read
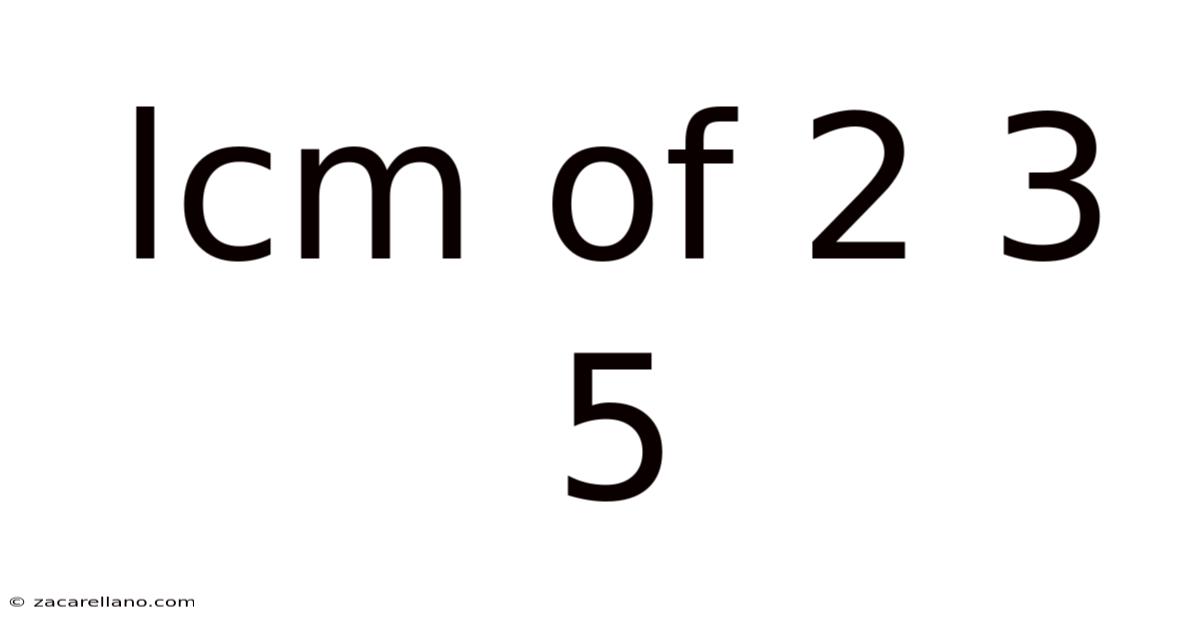
Table of Contents
Unveiling the Least Common Multiple (LCM) of 2, 3, and 5: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of a set of numbers might seem like a simple arithmetic task, but understanding the underlying principles reveals a fascinating glimpse into number theory and its applications. This article will explore the LCM of 2, 3, and 5 in detail, guiding you through various methods of calculation, explaining the mathematical concepts involved, and demonstrating its relevance in diverse fields. We'll also delve into some frequently asked questions and broader applications of LCM.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in mathematics, crucial for simplifying fractions, solving problems involving cycles, and understanding rhythmic patterns. While calculating the LCM of small numbers like 2, 3, and 5 is straightforward, grasping the underlying principles empowers you to tackle more complex scenarios.
Methods for Calculating the LCM of 2, 3, and 5
Several methods can be used to determine the LCM of 2, 3, and 5. Let's explore three common approaches:
1. Listing Multiples:
This method involves listing the multiples of each number until a common multiple is found.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30…
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
- Multiples of 5: 5, 10, 15, 20, 25, 30…
By comparing the lists, we observe that the smallest common multiple is 30. Therefore, the LCM(2, 3, 5) = 30. While simple for small numbers, this method becomes cumbersome with larger numbers.
2. Prime Factorization Method:
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
- Prime factorization of 2: 2¹
- Prime factorization of 3: 3¹
- Prime factorization of 5: 5¹
To find the LCM, we take the highest power of each prime factor present in the factorizations:
LCM(2, 3, 5) = 2¹ × 3¹ × 5¹ = 30
This method is more efficient than listing multiples, particularly when dealing with larger numbers.
3. Using the Greatest Common Divisor (GCD):
The LCM and GCD (greatest common divisor) are related through the formula:
LCM(a, b) × GCD(a, b) = a × b
While this formula directly applies to two numbers, we can extend it to multiple numbers by calculating the LCM iteratively. First, find the LCM of 2 and 3. The GCD(2,3) is 1. Therefore:
LCM(2,3) = (2 × 3) / GCD(2,3) = 6
Now, find the LCM of 6 and 5. The GCD(6,5) is 1. Therefore:
LCM(6,5) = (6 × 5) / GCD(6,5) = 30
Thus, LCM(2, 3, 5) = 30. This method is particularly useful when working with larger numbers where prime factorization might become more complex.
Mathematical Significance and Applications of LCM
The LCM is not merely a computational exercise; it holds significant mathematical importance and finds practical applications in various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves determining the LCM of the denominators. For example, adding 1/2 + 1/3 + 1/5 requires finding the LCM of 2, 3, and 5 (which is 30), allowing us to rewrite the fractions with a common denominator for easy addition.
-
Cyclic Events: LCM is crucial for determining when cyclic events will coincide. Imagine three different types of machines with cycles of 2, 3, and 5 hours respectively. The LCM (30 hours) indicates when all three machines will complete a full cycle simultaneously. This principle applies to scheduling, traffic light synchronization, and astronomical phenomena.
-
Rhythmic Patterns: In music theory, the LCM helps determine the least common denominator of rhythmic patterns. This allows musicians to create harmonious and complex rhythms by identifying points where different rhythmic patterns align.
-
Modular Arithmetic: The LCM plays a critical role in modular arithmetic, which is used in cryptography and computer science. Understanding the LCM helps to solve congruences and find solutions in systems of modular equations.
-
Abstract Algebra: LCM is a concept that extends beyond integers to more abstract algebraic structures, such as rings and ideals. In these contexts, it helps in understanding the structure and properties of these algebraic objects.
Beyond the Basics: Expanding the Concept
While this article focuses on the LCM of 2, 3, and 5, the concepts extend to any set of integers, even those with common factors. The prime factorization method remains particularly powerful in handling such cases. For example, consider finding the LCM of 6, 15, and 10:
- Prime factorization of 6: 2 × 3
- Prime factorization of 15: 3 × 5
- Prime factorization of 10: 2 × 5
The LCM(6, 15, 10) = 2 × 3 × 5 = 30
Notice that even though 6, 15, and 10 share common factors, the process remains consistent. The highest power of each prime factor is used to build the LCM.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are related but represent different aspects of the relationship between numbers.
-
Q: Can the LCM be larger than the numbers involved?
- A: Yes, the LCM is always greater than or equal to the largest of the numbers.
-
Q: Is there a formula for finding the LCM of more than two numbers?
- A: While there isn't a single concise formula like for two numbers, the prime factorization method provides a systematic approach for finding the LCM of any number of integers. The iterative GCD method can also be used.
-
Q: Why is the LCM important in real-world applications?
- A: The LCM is essential for solving problems involving cyclic events, rhythmic patterns, and scheduling tasks, as well as ensuring consistent measurements and calculations in various fields.
Conclusion
The LCM of 2, 3, and 5, while seemingly a simple problem, unveils a wealth of mathematical concepts and practical applications. Understanding the various methods for calculating LCM, such as listing multiples, prime factorization, and utilizing the GCD, empowers you to tackle more complex scenarios. The significance of LCM extends far beyond basic arithmetic, enriching our understanding of number theory and its relevance in diverse areas, from music and scheduling to advanced mathematics and computer science. The principles learned here provide a foundation for further exploration of number theory and its vast applications in the world around us. The seemingly simple act of finding the LCM(2,3,5) = 30 provides a gateway to a fascinating realm of mathematical understanding.
Latest Posts
Latest Posts
-
Independent And Dependent Clauses Quiz
Sep 15, 2025
-
Demand And Quantity Demanded Difference
Sep 15, 2025
-
Explain The Kinetic Molecular Theory
Sep 15, 2025
-
Rna Is Produced By Blank
Sep 15, 2025
-
Organic Chemistry Acids And Bases
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.