Lcm Of 24 And 18
zacarellano
Sep 11, 2025 · 6 min read
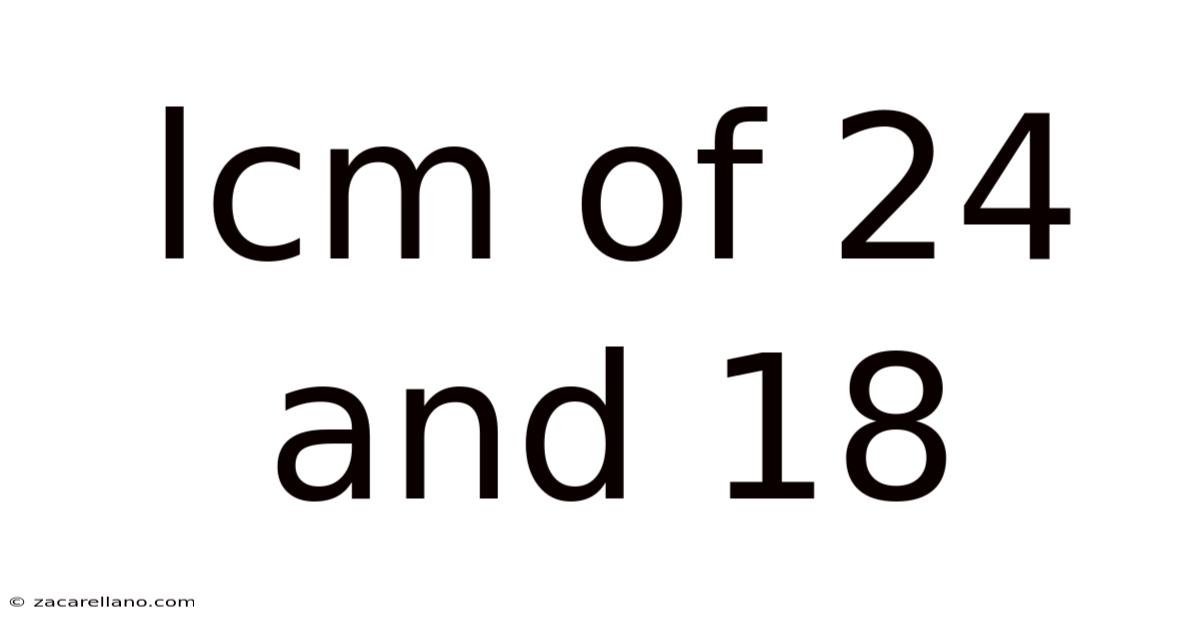
Table of Contents
Finding the Least Common Multiple (LCM) of 24 and 18: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 24 and 18, might seem like a simple arithmetic task. However, understanding the underlying concepts and different methods for calculating the LCM provides a deeper understanding of number theory and its applications in various fields, from scheduling problems to music theory. This comprehensive guide will not only show you how to find the LCM of 24 and 18 but also explore the various techniques involved, explain the underlying mathematical principles, and address common questions.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3. Understanding LCM is crucial in various mathematical applications, including simplifying fractions, solving problems involving periodic events, and even in music theory (for determining the least common denominator of musical intervals).
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240…
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180…
By comparing the lists, we can see that the smallest multiple common to both 24 and 18 is 72. Therefore, the LCM(24, 18) = 72. While this method is simple for smaller numbers, it becomes less efficient for larger numbers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It's based on finding the prime factorization of each number. The prime factorization of a number is the expression of that number as a product of its prime factors.
-
Find the prime factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3¹
-
Find the prime factorization of 18: 18 = 2 x 3 x 3 = 2¹ x 3²
-
Identify the highest power of each prime factor: The prime factors present are 2 and 3. The highest power of 2 is 2³ (from the factorization of 24), and the highest power of 3 is 3² (from the factorization of 18).
-
Multiply the highest powers together: LCM(24, 18) = 2³ x 3² = 8 x 9 = 72
This method is far more efficient for larger numbers, as it avoids the need to list out numerous multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. There's a formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
-
Find the GCD of 24 and 18: We can use the Euclidean algorithm to find the GCD.
- 24 = 1 x 18 + 6
- 18 = 3 x 6 + 0 The last non-zero remainder is 6, so GCD(24, 18) = 6.
-
Apply the formula: LCM(24, 18) = (24 x 18) / 6 = 432 / 6 = 72
This method is efficient, particularly when dealing with larger numbers where finding the prime factorization might be more challenging. The Euclidean algorithm for finding the GCD is relatively straightforward and computationally less intensive than extensive prime factorization for large numbers.
Method 4: Using Venn Diagrams (Visual Approach)
Venn diagrams offer a visual way to understand the relationship between the factors of two numbers and finding their LCM.
-
Prime Factorization: As before, we find the prime factorization of 24 (2³ x 3¹) and 18 (2¹ x 3²).
-
Venn Diagram: Draw two overlapping circles, one for 24 and one for 18.
-
Populate the Diagram: Place the common prime factors (in this case, 2 and 3) in the overlapping region. Place the unique prime factors in the non-overlapping regions. The highest power of each prime factor is used. Therefore:
- Overlapping region: 2¹ (since it’s the lowest power present in both numbers)
- Circle 24: 2² (2³ - 2¹ = 2²)
- Circle 18: 3¹ (3² - 3¹ = 3¹)
-
Calculate LCM: Multiply all the numbers in the Venn Diagram. This gives you: 2¹ x 2² x 3¹ = 2³ x 3¹ = 8 x 3 = 24 x 3 = 72.
Explanation of the Mathematical Principles
The LCM's existence is guaranteed by the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers (up to the order of factors). The LCM calculation leverages this uniqueness. By considering the highest powers of each prime factor present in the numbers, we ensure that the resulting number is divisible by both original numbers, and it's the smallest such number.
Applications of LCM
The LCM has numerous applications across various fields:
-
Scheduling: Imagine two buses arrive at a bus stop every 24 minutes and 18 minutes respectively. The LCM (72 minutes) tells us when they will arrive together again.
-
Fraction Arithmetic: Finding the LCM of the denominators is crucial when adding or subtracting fractions.
-
Music Theory: LCM helps find the least common denominator of musical rhythms and note values.
-
Modular Arithmetic: The LCM plays a role in solving problems involving modular arithmetic, a branch of mathematics used in cryptography and computer science.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers are relatively prime (their GCD is 1)?
- A: If the GCD is 1, then the LCM is simply the product of the two numbers.
-
Q: Can I find the LCM of more than two numbers?
- A: Yes, you can extend the methods (prime factorization or GCD-based methods) to find the LCM of more than two numbers. For prime factorization, consider the highest power of each prime factor present in all numbers.
-
Q: Why is the LCM important in real-world applications?
- A: The LCM helps in synchronizing events that occur periodically, simplifies complex calculations (like adding fractions), and is fundamental to various mathematical concepts used in computer science, music, and engineering.
-
Q: What’s the difference between LCM and GCD?
- A: The LCM is the smallest common multiple of two or more numbers, while the GCD is the largest common divisor. They are related through the formula: LCM(a,b) = (|a*b|)/GCD(a,b).
Conclusion
Finding the least common multiple of 24 and 18, or any two numbers, isn't just about getting the answer (72). It's about understanding the fundamental principles of number theory and appreciating the diverse applications of this seemingly simple concept. Mastering different methods – listing multiples, prime factorization, using the GCD, and even the visual approach of Venn diagrams – provides a robust understanding and makes tackling more complex problems easier. From scheduling to fraction arithmetic and beyond, the LCM proves to be a vital tool in various mathematical and real-world contexts. Remember to choose the method that best suits the numbers you are working with, prioritizing efficiency and understanding.
Latest Posts
Latest Posts
-
Alternative Form Of A Derivative
Sep 12, 2025
-
Short Run Aggregate Supply Graph
Sep 12, 2025
-
Geometric Series Partial Sum Formula
Sep 12, 2025
-
Transpose Of A Matrix Product
Sep 12, 2025
-
Converting Decimals To Fractions Worksheet
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.