Lcm Of 25 And 30
zacarellano
Sep 17, 2025 · 6 min read
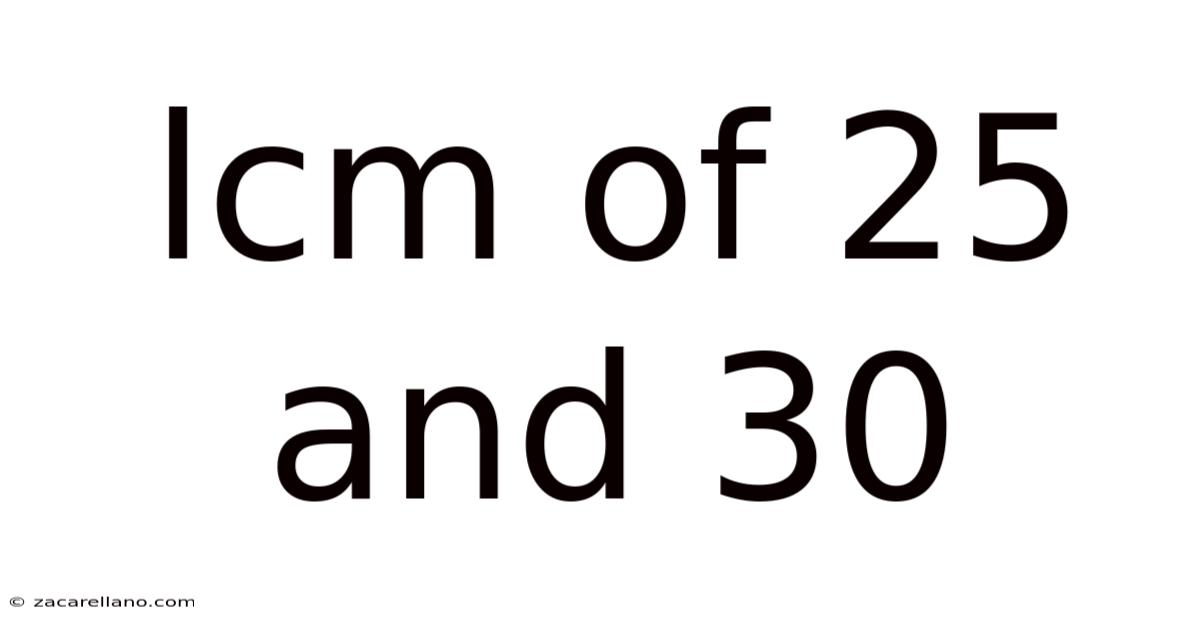
Table of Contents
Finding the LCM of 25 and 30: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simple fraction addition to complex algebraic manipulations. This comprehensive guide will explore the LCM of 25 and 30, explaining different methods to calculate it and providing a deep understanding of the underlying principles. We'll cover the methods in detail, addressing common misconceptions and building a solid foundation in this important area of number theory. This guide is perfect for students looking to solidify their understanding or anyone curious about the fascinating world of number theory.
Understanding Least Common Multiple (LCM)
Before diving into the calculation for the LCM of 25 and 30, let's define what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
The LCM is a critical concept in various mathematical operations, including:
- Adding and Subtracting Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Solving Problems Involving Ratios and Proportions: Understanding LCM helps in dealing with problems involving multiples and ratios.
- Scheduling and Pattern Recognition: LCM is useful in solving problems related to cyclical events, such as determining when two events will occur simultaneously.
- Modular Arithmetic: LCM plays a significant role in modular arithmetic, a branch of number theory with numerous applications in cryptography and computer science.
Method 1: Listing Multiples
The simplest method to find the LCM of 25 and 30 is by listing their multiples until a common multiple is found. Let's start with the multiples of 25:
25, 50, 75, 100, 125, 150, 175, 200, 225, 250, 275, 300...
Now, let's list the multiples of 30:
30, 60, 90, 120, 150, 180, 210, 240, 270, 300...
By comparing the two lists, we can see that the smallest common multiple is 150. Therefore, the LCM of 25 and 30 is 150. This method is straightforward for smaller numbers but can become cumbersome for larger numbers.
Method 2: Prime Factorization
The prime factorization method is a more efficient way to find the LCM, especially for larger numbers. This method involves breaking down each number into its prime factors. Remember, a prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Let's find the prime factorization of 25 and 30:
- 25: 5 x 5 = 5²
- 30: 2 x 3 x 5
To find the LCM using prime factorization, we follow these steps:
-
Identify the prime factors of each number: We've already done this: 25 = 5² and 30 = 2 x 3 x 5.
-
Select the highest power of each prime factor present in the factorizations: The prime factors present are 2, 3, and 5. The highest power of 2 is 2¹ (from 30), the highest power of 3 is 3¹ (from 30), and the highest power of 5 is 5² (from 25).
-
Multiply the highest powers together: LCM(25, 30) = 2¹ x 3¹ x 5² = 2 x 3 x 25 = 150
Therefore, the LCM of 25 and 30, using prime factorization, is 150. This method is more efficient and less prone to errors, particularly when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b) = (a x b) / GCD(a, b)
Let's use this formula to find the LCM of 25 and 30. First, we need to find the GCD of 25 and 30. We can use the Euclidean algorithm for this:
- Divide the larger number (30) by the smaller number (25): 30 ÷ 25 = 1 with a remainder of 5.
- Replace the larger number with the smaller number (25) and the smaller number with the remainder (5): 25 ÷ 5 = 5 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 5. Therefore, GCD(25, 30) = 5.
Now, let's apply the formula:
LCM(25, 30) = (25 x 30) / 5 = 750 / 5 = 150
Again, the LCM of 25 and 30 is 150. This method is particularly useful when dealing with larger numbers where listing multiples or prime factorization becomes tedious. The Euclidean algorithm provides an efficient way to compute the GCD.
Why Understanding LCM is Important
The LCM's importance extends beyond simple mathematical calculations. Its applications are widespread and crucial in various fields:
- Engineering and Construction: Calculating the lengths of materials required for projects that need repeated patterns or consistent spacing necessitates using LCM.
- Music Theory: The LCM plays a role in determining harmonic intervals and creating musical compositions.
- Computer Science: The LCM is utilized in algorithms for scheduling tasks and managing processes.
- Cryptography: LCM is a building block in some encryption algorithms.
A strong grasp of LCM empowers you to tackle complex problems efficiently and creatively, opening doors to more advanced mathematical concepts.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers, while the GCD (Greatest Common Divisor) is the largest number that divides both numbers without leaving a remainder. They are inversely related; a higher GCD means a lower LCM, and vice-versa.
Q: Can the LCM of two numbers be one of the numbers?
A: Yes, if one number is a multiple of the other, the LCM will be the larger number. For example, the LCM of 5 and 10 is 10.
Q: Is there a formula to directly calculate the LCM without using the GCD?
A: While the formula using GCD is efficient, there isn't a single direct formula that avoids prime factorization or other intermediate steps completely. The prime factorization method essentially provides a direct but indirect approach.
Q: How do I find the LCM of more than two numbers?
A: You can extend the prime factorization method. Find the prime factorization of each number, take the highest power of each prime factor, and multiply them together. You can also find the LCM of two numbers first and then find the LCM of that result and the next number, and so on.
Q: Why is the prime factorization method considered more efficient?
A: The prime factorization method avoids the potentially lengthy process of listing multiples, which becomes increasingly inefficient as numbers get larger. Prime factorization provides a structured and deterministic approach that scales better.
Conclusion
Finding the LCM of 25 and 30, as demonstrated through various methods, is not merely an exercise in arithmetic; it's a gateway to understanding fundamental mathematical principles. Mastering LCM calculations equips you with valuable skills applicable across diverse fields, from everyday problem-solving to advanced scientific applications. Whether you use the listing method, prime factorization, or the GCD approach, the result remains consistent: the LCM of 25 and 30 is 150. Choosing the best method depends on the numbers involved and your preference for different problem-solving strategies. Remember, understanding the underlying concepts, not just the answer, is key to mastering the LCM and other essential mathematical concepts. The more you practice and explore different methods, the more confident and proficient you'll become in your mathematical abilities.
Latest Posts
Latest Posts
-
Worksheet On Pronoun Antecedent Agreement
Sep 17, 2025
-
Four Components Of Natural Selection
Sep 17, 2025
-
Convolution Theorem In Laplace Transform
Sep 17, 2025
-
Opportunity Cost Of Holding Money
Sep 17, 2025
-
The Populist Party Apush Definition
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 25 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.