Lcm Of 3 And 8
zacarellano
Sep 14, 2025 · 6 min read
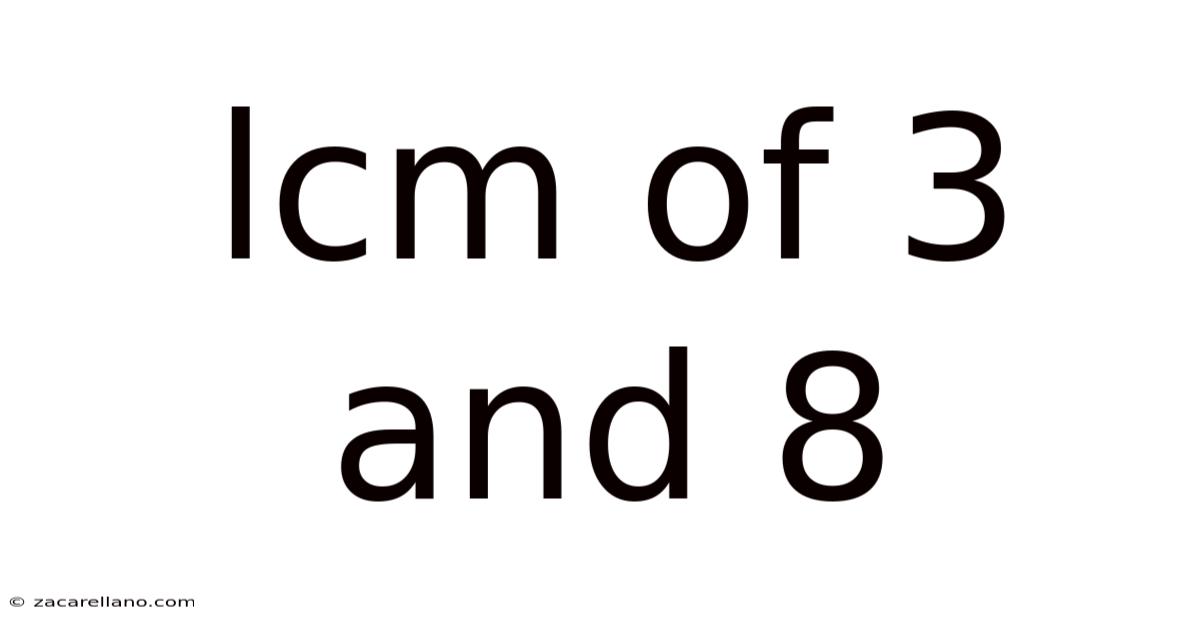
Table of Contents
Finding the LCM of 3 and 8: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers, like 3 and 8, might seem like a simple arithmetic task. However, understanding the underlying concepts and exploring different methods for calculating the LCM opens up a world of mathematical understanding, applicable not just to simple numbers but also to more complex scenarios in algebra and beyond. This article will guide you through the process of finding the LCM of 3 and 8, explaining various methods, their applications, and the broader mathematical principles involved. We'll delve into the fundamental concepts, explore multiple solution strategies, and even address some frequently asked questions.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 3 and 8 specifically, let's establish a solid foundation. The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 3 and 8. Let's list the multiples of each number:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 8: 8, 16, 24, 32, 40, 48...
By comparing the two lists, we can see that the smallest number appearing in both lists is 24. Therefore, the LCM of 3 and 8 is 24.
This method works well for small numbers but becomes cumbersome and inefficient when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient and works for larger numbers. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 3: 3 (3 is already a prime number)
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM using prime factorization:
- Identify all the prime factors: In this case, we have 2 and 3.
- Take the highest power of each prime factor: The highest power of 2 is 2³ (from the factorization of 8), and the highest power of 3 is 3¹ (from the factorization of 3).
- Multiply the highest powers together: 2³ x 3¹ = 8 x 3 = 24
Therefore, the LCM of 3 and 8 is 24, confirming the result from the previous method. This method is significantly more efficient for larger numbers because it avoids the need to list out numerous multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a formula connecting the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Let's use this method to find the LCM of 3 and 8:
- Find the GCD of 3 and 8: The GCD of 3 and 8 is 1 because 1 is the only number that divides both 3 and 8 without leaving a remainder.
- Apply the formula: LCM(3, 8) x GCD(3, 8) = 3 x 8 LCM(3, 8) x 1 = 24 LCM(3, 8) = 24
This method, while requiring an extra step to find the GCD, is also quite efficient, especially when dealing with larger numbers where finding the GCD might be easier than listing all multiples. Finding the GCD can be done using the Euclidean algorithm, which is a highly efficient method for larger numbers.
Method 4: Venn Diagram Approach (for Visual Learners)
For those who prefer a visual approach, a Venn diagram can be helpful. This method uses prime factorization implicitly.
- Prime factorize each number: 3 = 3; 8 = 2 x 2 x 2
- Represent prime factors in a Venn diagram: Draw two overlapping circles, one for 3 and one for 8. Place the prime factors in the appropriate sections. Since there are no common prime factors, 3 and 2³ will be in separate circles.
- Calculate LCM: Multiply all the numbers in the diagram together (including those in the overlapping section, even though it's empty in this case): 3 x 2 x 2 x 2 = 24
Applications of Finding the LCM
Finding the LCM has numerous applications in various areas of mathematics and beyond:
- Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to finding a common denominator.
- Scheduling: Determining when events will occur simultaneously. For example, if one event happens every 3 days and another every 8 days, the LCM helps determine when they both occur on the same day.
- Music Theory: Calculating the least common multiple of note durations is essential in music composition.
- Gear Ratios: In mechanical engineering, gear ratios and timing calculations often rely on the LCM.
- Modular Arithmetic: LCM plays a role in various concepts in number theory, particularly modular arithmetic.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, simply include all the prime factors from all the numbers and take the highest power of each. For the listing method, it becomes even more laborious but conceptually remains the same. The GCD method can also be extended but requires finding the GCD of multiple numbers.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are related through the formula: LCM(a, b) x GCD(a, b) = a x b.
-
Can the LCM of two numbers be smaller than one of the numbers? No, the LCM will always be greater than or equal to the larger of the two numbers.
-
What if the two numbers have no common factors other than 1? If the GCD of two numbers is 1 (meaning they are relatively prime or coprime), then their LCM is simply their product. This is the case with 3 and 8.
-
How can I calculate the LCM of very large numbers? For very large numbers, using the prime factorization method in conjunction with efficient algorithms for prime factorization is the most practical approach.
-
Are there any online calculators or software for finding the LCM? Yes, many online calculators and mathematical software packages can compute the LCM of any set of numbers.
Conclusion
Finding the LCM of 3 and 8, while seemingly simple, provides a valuable opportunity to explore fundamental mathematical concepts like prime factorization, the relationship between LCM and GCD, and various algorithmic approaches to problem-solving. Understanding these concepts isn't just about calculating a single value; it's about developing a deeper appreciation for the interconnectedness of mathematical ideas and their wide-ranging applications in diverse fields. The methods discussed here offer flexibility, allowing you to choose the most suitable approach based on the numbers involved and your preferred problem-solving style. Remember that the core principle of finding the LCM is about identifying the smallest number that is divisible by all the given numbers without any remainder. Mastering this concept opens doors to more advanced mathematical explorations.
Latest Posts
Latest Posts
-
Commas In Lists Of Adjectives
Sep 14, 2025
-
Is More Quickly Grammatically Correct
Sep 14, 2025
-
Square Root Of 3 Squared
Sep 14, 2025
-
Lcm Of 12 And 24
Sep 14, 2025
-
How To Fins The Slope
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.