Lcm Of 5 And 2
zacarellano
Sep 09, 2025 · 6 min read
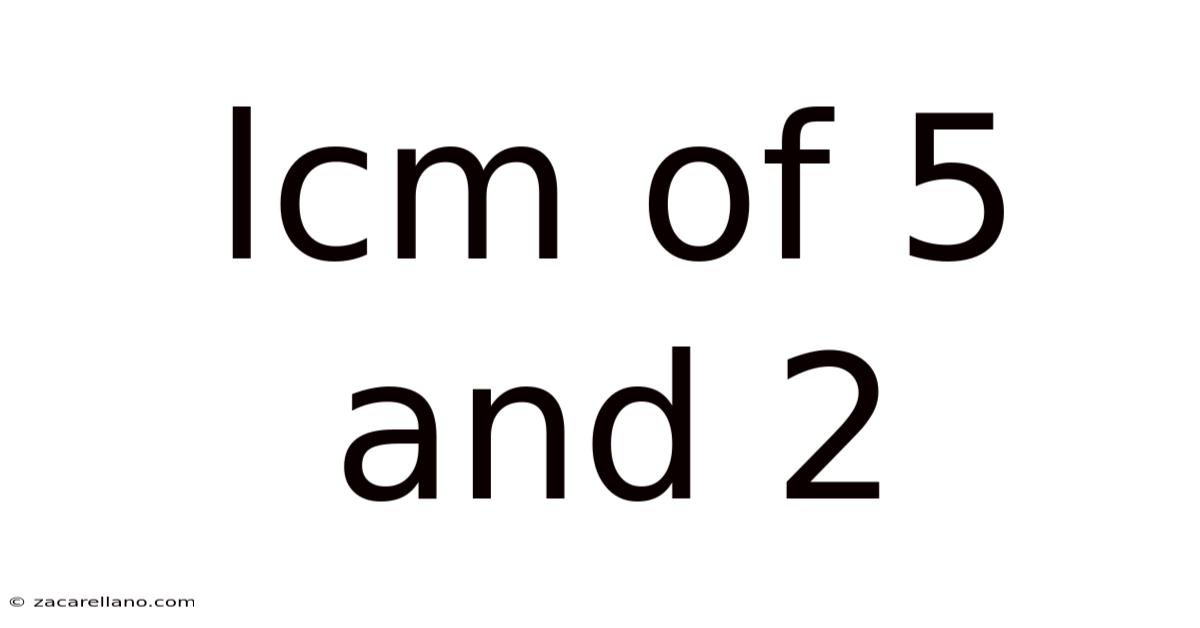
Table of Contents
Finding the Least Common Multiple (LCM) of 5 and 2: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 5 and 2. However, understanding the underlying concepts and different methods for calculating the LCM is crucial for mastering more complex mathematical problems. This comprehensive guide will not only show you how to find the LCM of 5 and 2 but also delve into the theoretical foundation, explore various calculation methods, and extend the concept to more complex scenarios. This will equip you with a solid understanding of LCM and its applications in various fields.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding multiples is key. Multiples of a number are the numbers you get when you multiply that number by any whole number (0, 1, 2, 3, and so on).
For example:
- Multiples of 5 are: 0, 5, 10, 15, 20, 25, 30, ...
- Multiples of 2 are: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ...
Notice that both lists contain the number 10. 10 is a common multiple of 5 and 2. However, it's not the least common multiple. It's the smallest common multiple that's greater than zero.
Calculating the LCM of 5 and 2: Three Methods
There are several ways to find the LCM of two numbers. Let's explore three common methods, using 5 and 2 as our example:
Method 1: Listing Multiples
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30…
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…
The smallest positive number that appears in both lists is 10. Therefore, the LCM of 5 and 2 is 10.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from those prime factors.
- Prime factorization of 5: 5 (5 is a prime number itself)
- Prime factorization of 2: 2 (2 is a prime number)
Since 5 and 2 are both prime numbers and have no common factors, the LCM is simply the product of the two numbers: 5 x 2 = 10.
Method 3: Using the Formula (LCM and GCD Relationship)
The least common multiple (LCM) and the greatest common divisor (GCD) of two numbers are intimately related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This can be expressed as a formula:
- LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD (Greatest Common Divisor) of 5 and 2. The GCD is the largest number that divides both 5 and 2 without leaving a remainder. In this case, the GCD of 5 and 2 is 1 (because 1 is the only positive integer that divides both 5 and 2).
Now, we can use the formula:
- LCM(5, 2) * GCD(5, 2) = 5 * 2
- LCM(5, 2) * 1 = 10
- LCM(5, 2) = 10
Therefore, the LCM of 5 and 2 is 10. This method is particularly useful when dealing with larger numbers where finding prime factors might be more time-consuming.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. Let's consider finding the LCM of 5, 2, and 3.
Method 1: Listing Multiples (Extended)
While feasible for small numbers, this method becomes cumbersome with more numbers. We'd need to list multiples of each number until we find the smallest common multiple:
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The smallest common multiple among the three lists is 30. Therefore, LCM(5, 2, 3) = 30.
Method 2: Prime Factorization (Extended)
This method is far more efficient for multiple numbers.
- Prime factorization of 5: 5
- Prime factorization of 2: 2
- Prime factorization of 3: 3
To find the LCM, we take the highest power of each prime factor present in the factorizations:
LCM(5, 2, 3) = 2¹ x 3¹ x 5¹ = 30
Method 3: Using the Formula (Extended - Iterative Approach)
The formula LCM(a, b) * GCD(a, b) = a * b doesn't directly extend to more than two numbers. Instead, we can use an iterative approach:
- Find the LCM of the first two numbers (e.g., LCM(5, 2) = 10).
- Find the LCM of the result and the next number (e.g., LCM(10, 3)). We can use either the listing method or prime factorization to find LCM(10,3). Prime factorization is easier:
- 10 = 2 x 5
- 3 = 3
- LCM(10,3) = 2 x 3 x 5 = 30
Therefore, LCM(5, 2, 3) = 30.
The Significance of LCM in Real-World Applications
While the concept of LCM might seem purely mathematical, it has practical applications in various fields:
- Scheduling: Imagine two buses arrive at a bus stop at different intervals. Finding the LCM of those intervals helps determine when both buses will arrive at the stop simultaneously.
- Project Management: Tasks within a project might have different completion times. LCM can help schedule tasks to optimize workflow and minimize idle time.
- Music: In music theory, LCM is used to determine when two musical phrases with different lengths will align rhythmically.
- Engineering: In gear systems, the LCM helps determine when gears with different numbers of teeth will align perfectly.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers evenly.
Q2: Can the LCM of two numbers ever be smaller than the larger of the two numbers?
A2: No. The LCM will always be greater than or equal to the largest of the two numbers.
Q3: Is there a limit to the number of integers for which we can find the LCM?
A3: No, the concept of LCM applies to any number of integers. While the listing method becomes impractical, prime factorization remains an efficient approach for finding the LCM of a large set of integers.
Q4: What if one of the numbers is zero?
A4: The LCM of any set of numbers that includes zero is undefined. The concept of multiples does not apply to zero in the context of LCM calculations.
Conclusion
Finding the least common multiple (LCM) of numbers, even seemingly simple pairs like 5 and 2, provides a foundational understanding of important mathematical concepts. This guide has explored different methods for calculating the LCM, highlighted the relationship between LCM and GCD, and demonstrated the practical applications of LCM in various real-world scenarios. By mastering these techniques, you'll be well-equipped to tackle more complex mathematical problems and appreciate the broad utility of this seemingly simple concept. Remember, understanding the why behind the calculations is as important as knowing the how. This deeper understanding will solidify your mathematical foundation and empower you to solve more challenging problems in the future.
Latest Posts
Latest Posts
-
The Budda Sitting In Meditatioon
Sep 09, 2025
-
Examples Of Dihybrid Cross Problems
Sep 09, 2025
-
Example Of A Linkage Institution
Sep 09, 2025
-
Demand And Supply Graph Practice
Sep 09, 2025
-
Syncretism Definition Ap World History
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.