Lcm Of 5 And 5
zacarellano
Sep 24, 2025 · 5 min read
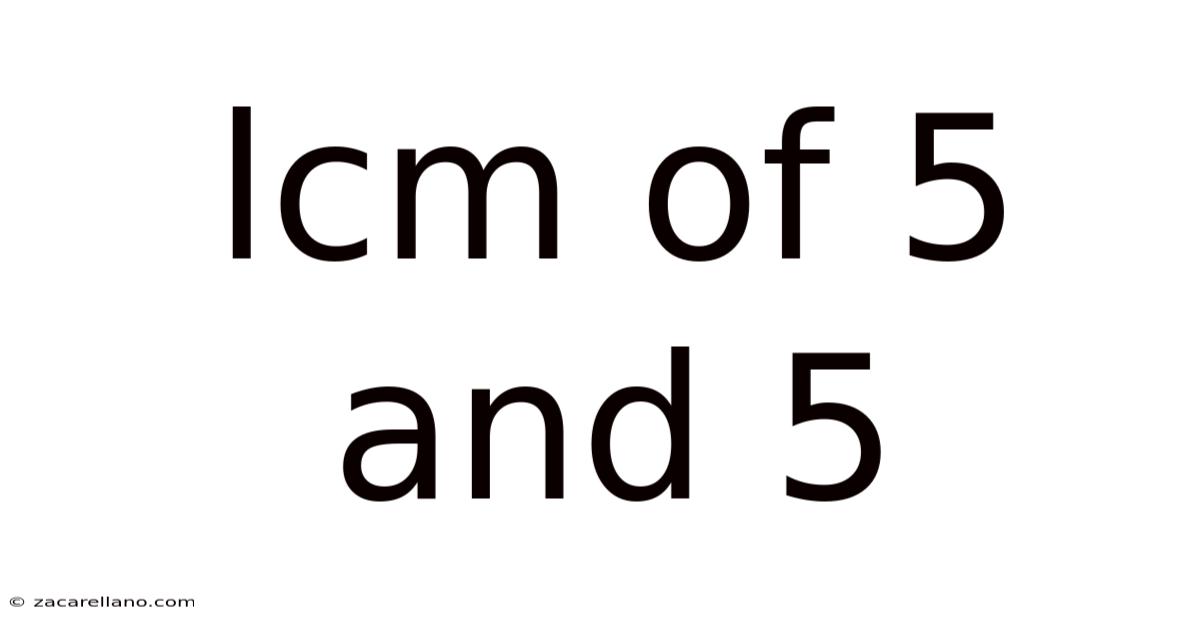
Table of Contents
Finding the Least Common Multiple (LCM) of 5 and 5: A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem trivial for simple numbers like 5 and 5. However, understanding the underlying concepts behind LCM calculations is crucial for grasping more complex mathematical operations and problem-solving in areas like algebra, calculus, and even computer science. This article will not only calculate the LCM of 5 and 5 but also explore the various methods for determining the LCM of any two (or more) numbers, delving into the theoretical foundations and practical applications. We'll also address frequently asked questions to ensure a comprehensive understanding of this fundamental mathematical concept.
Understanding Least Common Multiple (LCM)
Before we dive into the specific calculation, let's define what the least common multiple actually is. The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 5 and 5
Now, let's address the specific problem: finding the LCM of 5 and 5. This is a particularly straightforward case because both numbers are identical. Since 5 is a multiple of 5 (5 x 1 = 5), the smallest positive integer that is a multiple of both 5 and 5 is simply 5 itself.
Therefore, the LCM of 5 and 5 is 5.
Methods for Calculating LCM
While the LCM of 5 and 5 was easily determined by inspection, let's examine more general methods applicable to any pair of numbers. These methods are particularly useful when dealing with larger or less obvious numbers.
1. Listing Multiples Method:
This is the most intuitive approach, especially for smaller numbers. You list out the multiples of each number until you find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
As you can see, the smallest number appearing in both lists is 5.
2. Prime Factorization Method:
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
Since both numbers have only one prime factor, 5, and the highest power of 5 is 5<sup>1</sup>, the LCM is 5.
3. Greatest Common Divisor (GCD) Method:
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The formula relating LCM and GCD is:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where:
aandbare the two numbers.GCD(a, b)is the greatest common divisor ofaandb.|a * b|denotes the absolute value of the product of a and b.
For the numbers 5 and 5:
- The GCD of 5 and 5 is 5 (5 divides both 5 and 5 evenly).
- LCM(5, 5) = (|5 * 5|) / 5 = 25 / 5 = 5
This method confirms our previous result.
Applications of LCM
The concept of LCM has widespread applications in various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if bus A arrives every 10 minutes and bus B arrives every 15 minutes, the LCM helps find when both buses arrive at the same time.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is essentially the LCM of the denominators.
-
Music Theory: Calculating the rhythmic relationships between different musical notes and phrases.
-
Computer Science: In algorithms and data structures, LCM finds applications in areas like cycle detection and array manipulation.
Further Exploration: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For the prime factorization method, you would consider all prime factors from all numbers and use the highest power of each. For the GCD method, you would need to iteratively calculate the LCM of pairs of numbers.
Frequently Asked Questions (FAQ)
Q: Is the LCM of any number and itself always the number itself?
A: Yes, the LCM of any number and itself is always the number itself. This is because any number is a multiple of itself.
Q: What if one of the numbers is zero?
A: The LCM of any number and zero is undefined. Zero has infinitely many multiples, making it impossible to define a least common multiple.
Q: How do I calculate the LCM of three or more numbers?
A: You can use the prime factorization method by combining all prime factors from all numbers and using the highest power of each. Alternatively, you can calculate the LCM iteratively: find the LCM of the first two numbers, then find the LCM of that result and the third number, and so on.
Q: What is the relationship between the LCM and the GCD?
A: For any two positive integers a and b, the product of their LCM and GCD is equal to the product of the two numbers: LCM(a, b) * GCD(a, b) = a * b. This relationship is very useful in calculations.
Conclusion
Finding the LCM of 5 and 5, while seemingly trivial, provides a solid foundation for understanding the broader concept of least common multiples. This article has explored various methods for calculating the LCM, highlighting their applicability to different scenarios. Beyond the simple example, the LCM plays a significant role in various mathematical and practical applications, showcasing its importance as a fundamental concept in number theory. Understanding LCM is not merely about finding a single answer but about grasping the underlying principles that govern the relationships between integers and their multiples. This knowledge empowers us to tackle more complex mathematical problems with confidence and efficiency.
Latest Posts
Latest Posts
-
Is Russia Enemy Of Us
Sep 24, 2025
-
Organic Chemistry Ii Practice Exam
Sep 24, 2025
-
Is Hydrolysis Anabolic Or Catabolic
Sep 24, 2025
-
Light Microscope Electron Microscope Comparison
Sep 24, 2025
-
Math Challenges For 6th Graders
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.