Lcm Of 7 And 3
zacarellano
Sep 12, 2025 · 6 min read
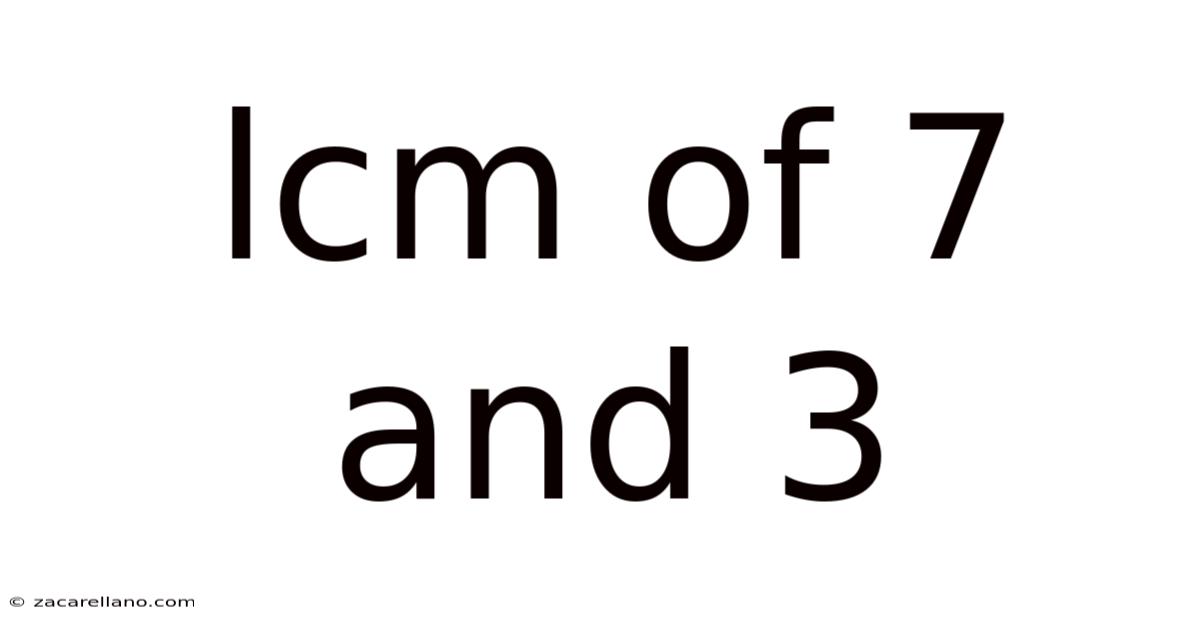
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 3: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts provides a solid foundation for more advanced mathematical concepts. This article will explore how to calculate the LCM of 7 and 3, explain the different methods available, and delve into the theoretical underpinnings of LCMs, providing a comprehensive understanding suitable for students of various levels. We’ll also touch upon applications of LCMs in real-world scenarios.
Understanding Least Common Multiple (LCM)
Before we tackle the LCM of 7 and 3 specifically, let's define what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the original numbers as factors. This concept is crucial in various areas of mathematics, from simplifying fractions to solving problems involving cycles and periodic events.
Think of it like finding the smallest common ground for two or more repeating events. If one event repeats every 7 days and another every 3 days, the LCM will tell us when both events will coincide again.
Methods for Calculating LCM
Several methods exist for calculating the LCM, each with its own advantages and disadvantages. Let's examine the most common ones:
1. Listing Multiples Method:
This is the most straightforward approach, especially for smaller numbers like 7 and 3. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, ...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30,...
As you can see, the smallest number that appears in both lists is 21. Therefore, the LCM of 7 and 3 is 21.
This method is simple and intuitive, but it becomes less efficient when dealing with larger numbers. Imagine trying to find the LCM of 147 and 252 using this method – it would be quite tedious!
2. Prime Factorization Method:
This method is more efficient for larger numbers. It involves breaking down each number into its prime factors – prime numbers that multiply to give the original number.
- Prime factorization of 7: 7 (7 is a prime number itself)
- Prime factorization of 3: 3 (3 is also a prime number)
Now, we consider the highest power of each prime factor present in either factorization:
- The highest power of 3 is 3¹ = 3
- The highest power of 7 is 7¹ = 7
We multiply these highest powers together: 3 x 7 = 21. Therefore, the LCM of 7 and 3 is 21.
3. Greatest Common Divisor (GCD) Method:
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The relationship is expressed as:
LCM(a, b) * GCD(a, b) = a * b
where 'a' and 'b' are the two numbers.
To use this method:
- Find the GCD of 7 and 3: The GCD of 7 and 3 is 1 (since 1 is the only common divisor).
- Apply the formula: LCM(7, 3) * GCD(7, 3) = 7 * 3 LCM(7, 3) * 1 = 21 LCM(7, 3) = 21
This method is particularly useful when dealing with larger numbers, as efficient algorithms exist for finding the GCD (like the Euclidean algorithm).
LCM of 7 and 3: A Detailed Explanation
We've already determined that the LCM of 7 and 3 is 21 using different methods. Let's solidify this understanding with a detailed explanation:
- 7 is a prime number. It's only divisible by 1 and itself.
- 3 is also a prime number. It's only divisible by 1 and itself.
- Since 7 and 3 share no common factors other than 1, their LCM is simply their product: 7 * 3 = 21. This is a specific case of the general rule that the LCM of two coprime numbers (numbers with a GCD of 1) is their product.
This simple example highlights the core principle: the LCM represents the smallest number that incorporates all the prime factors of the original numbers, considering their highest powers.
Applications of LCM in Real-World Scenarios
The concept of LCM extends beyond the realm of abstract mathematics and finds practical applications in various scenarios:
-
Scheduling: Imagine two buses leaving a terminal at different intervals. One bus departs every 7 minutes, and the other departs every 3 minutes. The LCM (21 minutes) tells us when both buses will depart simultaneously again.
-
Calendars: Determining when specific days of the week coincide (e.g., when a specific weekday falls on a particular date in a given year).
-
Manufacturing: Coordinating production lines with different cycle times. For example, if one machine completes a cycle every 7 seconds and another every 3 seconds, the LCM determines when both machines will complete their cycles simultaneously.
-
Music: Finding the least common multiple of the durations of different musical phrases or notes to synchronize musical patterns or compositions.
-
Construction: Aligning construction elements with varying repeating patterns.
Frequently Asked Questions (FAQ)
Q: What if I have more than two numbers? How do I find the LCM?
A: You can extend the prime factorization method or the GCD method to handle multiple numbers. For prime factorization, you consider the highest power of each prime factor present in any of the factorizations. For the GCD method, you can find the LCM iteratively: first find the LCM of two numbers, then find the LCM of that result and the next number, and so on.
Q: Is there a formula for finding the LCM of any two numbers?
A: Yes, the formula relating the LCM and GCD is: LCM(a, b) = (a * b) / GCD(a, b). Remember, you need to find the GCD first.
Q: Can the LCM of two numbers be smaller than both numbers?
A: No. The LCM of two numbers will always be greater than or equal to the larger of the two numbers.
Q: What if one of the numbers is 0?
A: The LCM of any number and 0 is undefined, since 0 is a divisor of all integers.
Conclusion
Finding the LCM of 7 and 3, while seemingly trivial, serves as a gateway to understanding a fundamental concept in number theory with widespread applications. Through the methods discussed—listing multiples, prime factorization, and the GCD method—we've not only calculated the LCM but also gained insights into the underlying mathematical principles. This deeper understanding equips you to tackle more complex problems involving LCMs and enhances your overall mathematical reasoning. Remember that understanding the "why" behind the calculations is as important as knowing the "how." The more you explore these concepts, the more you will appreciate their elegance and power.
Latest Posts
Latest Posts
-
15 Required Supreme Court Cases
Sep 12, 2025
-
Was Meiji Restoration In China
Sep 12, 2025
-
Exponents With A Negative Base
Sep 12, 2025
-
Ap Gov Unit 1 Quizlet
Sep 12, 2025
-
Gcf Of 28 And 12
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.