Lcm Of 8 And 11
zacarellano
Sep 15, 2025 · 5 min read
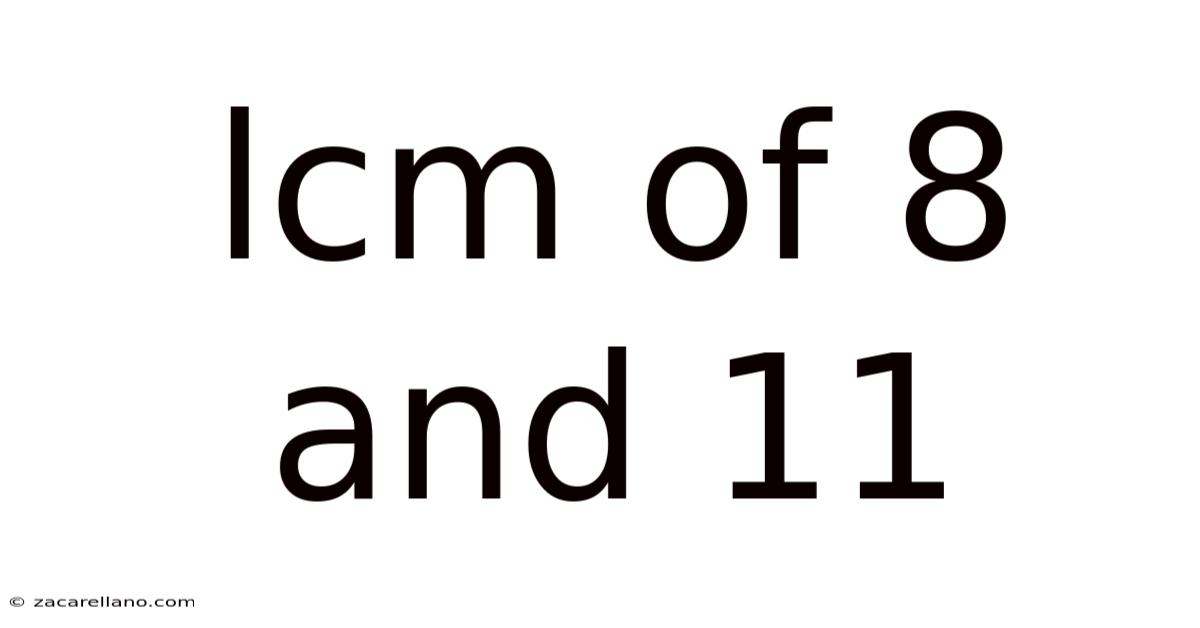
Table of Contents
Finding the Least Common Multiple (LCM) of 8 and 11: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation is crucial for a strong foundation in mathematics. This comprehensive guide will delve into the LCM of 8 and 11, exploring various approaches and providing a deeper understanding of this fundamental concept. We'll cover the definition of LCM, step-by-step calculation methods, the application of prime factorization, and finally address some frequently asked questions. This will equip you not just with the answer for the LCM of 8 and 11, but also with the tools to tackle similar problems with ease.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the integers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3. Finding the LCM is a fundamental concept used in various areas of mathematics, including simplifying fractions, solving problems involving time intervals, and working with ratios and proportions.
Methods for Calculating LCM
Several methods can be used to determine the LCM of two or more numbers. Let's explore the most common ones, applying them to find the LCM of 8 and 11:
1. Listing Multiples Method
This straightforward method involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96...
- Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110...
Notice that the smallest multiple common to both lists is 88. Therefore, the LCM of 8 and 11 is 88. This method is effective for smaller numbers but can become cumbersome for larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 8: 2³ (8 = 2 x 2 x 2)
- Prime factorization of 11: 11¹ (11 is a prime number)
Since 8 and 11 share no common prime factors, the LCM is simply the product of their prime factorizations: 2³ x 11¹ = 8 x 11 = 88. This method is generally preferred for its efficiency and clear demonstration of the underlying mathematical principles.
3. Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are related through the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
First, we need to find the GCD of 8 and 11. The GCD is the largest number that divides both 8 and 11 without leaving a remainder. Since 8 and 11 are relatively prime (they share no common factors other than 1), their GCD is 1.
Now, we can use the formula:
LCM(8, 11) = (|8 x 11|) / GCD(8, 11) = (88) / 1 = 88
This method highlights the interconnectedness of LCM and GCD, demonstrating how knowledge of one can be used to efficiently calculate the other.
Why is the LCM Important?
Understanding and calculating the LCM is essential for various mathematical applications, including:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves determining the LCM of the denominators.
-
Solving Problems Involving Cycles: Imagine two cycles, one repeating every 8 seconds and the other every 11 seconds. The LCM (88 seconds) represents the time when both cycles will coincide again.
-
Ratio and Proportion Problems: The LCM is crucial in simplifying ratios and solving problems involving proportions.
-
Modular Arithmetic: The concept of LCM finds significant use in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then include the highest power of each prime factor present in the overall LCM calculation. For the listing multiples method, you would list the multiples of each number until a common multiple is found for all numbers. The GCD method can also be extended using iterative approaches.
Frequently Asked Questions (FAQ)
Q: What if the two numbers share common factors? How does that affect the LCM calculation?
A: If the numbers share common factors, the prime factorization method will efficiently handle this. The common factors will contribute only their highest power to the final LCM calculation. The GCD method explicitly accounts for the shared factors, making it efficient regardless of whether the numbers share common factors.
Q: Is there a quickest way to find the LCM?
A: The prime factorization method is generally the most efficient for larger numbers. For smaller numbers, the listing multiples method might be quicker if you recognize the common multiple early.
Q: Can the LCM of two numbers ever be smaller than the larger of the two numbers?
A: No. The LCM will always be greater than or equal to the larger of the two numbers.
Q: What is the LCM of 0 and any other number?
A: The LCM of 0 and any other number is undefined. The concept of LCM only applies to positive integers.
Conclusion
Determining the LCM of 8 and 11, as we have demonstrated, is straightforward using several methods. Whether you employ the listing multiples method, the prime factorization method, or the GCD-based method, the result remains consistent: the LCM of 8 and 11 is 88. However, grasping the underlying concepts and the different approaches allows you to efficiently tackle LCM problems of increasing complexity. Understanding LCM isn't just about memorizing formulas; it's about gaining a deeper appreciation of the fundamental principles governing number theory and its application in diverse mathematical contexts. The ability to confidently calculate LCMs is a valuable asset in your mathematical toolkit, opening doors to a more profound understanding of numerical relationships and their applications.
Latest Posts
Latest Posts
-
Division With Powers Of 10
Sep 15, 2025
-
Is X Into The Page
Sep 15, 2025
-
Is 259 A Prime Number
Sep 15, 2025
-
Ghost Dance Ap World History
Sep 15, 2025
-
Ap Psych Theories Of Emotion
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.