Negative 1 Minus Negative 4
zacarellano
Sep 19, 2025 · 6 min read
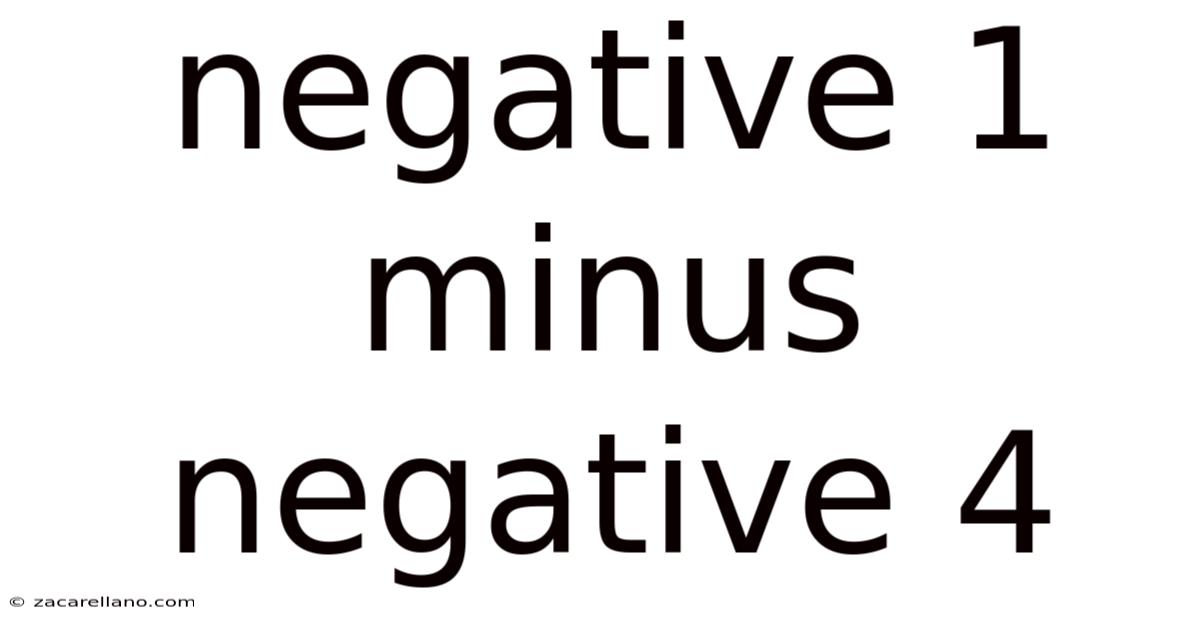
Table of Contents
Decoding -1 - (-4): A Deep Dive into Integer Subtraction
Understanding integer subtraction, particularly when dealing with negative numbers, can be tricky. This article will thoroughly explain the concept behind the calculation "-1 - (-4)," breaking it down step-by-step and exploring the underlying mathematical principles. We'll cover various methods for solving this type of problem, address common misconceptions, and explore real-world applications to solidify your understanding. By the end, you'll not only know the answer but also possess a strong grasp of integer arithmetic.
Introduction: The Basics of Integer Subtraction
Integers are whole numbers, including zero, and their negative counterparts (...,-3, -2, -1, 0, 1, 2, 3,...). Subtracting integers involves finding the difference between two numbers. While subtracting positive numbers is relatively straightforward, subtracting negative numbers introduces a layer of complexity that requires understanding the concept of opposites or additive inverses. The expression "-1 - (-4)" exemplifies this complexity. This seemingly simple equation actually encapsulates fundamental rules governing arithmetic operations with negative numbers. Mastering this concept is crucial for further mathematical endeavors, including algebra, calculus, and beyond.
Understanding Additive Inverses
Before tackling "-1 - (-4)," it's vital to grasp the concept of additive inverses. The additive inverse of a number is the number that, when added to the original number, results in zero. For example:
- The additive inverse of 5 is -5 (5 + (-5) = 0)
- The additive inverse of -3 is 3 (-3 + 3 = 0)
- The additive inverse of 0 is 0 (0 + 0 = 0)
This concept is key to understanding subtraction with negative numbers. Subtracting a number is the same as adding its additive inverse. This is often summarized as the rule: a - b = a + (-b)
Step-by-Step Solution to -1 - (-4)
Applying this crucial rule to our problem, "-1 - (-4)," we can rewrite the expression as:
-1 + (-(-4))
Now, the double negative (-(-4)) simplifies. The additive inverse of -4 is 4. Therefore:
-1 + 4
This is a simple addition problem. We are adding a negative number (-1) and a positive number (4). Think of it as starting at -1 on a number line and moving 4 units to the right. This leads us to the solution:
-1 + 4 = 3
Therefore, -1 - (-4) = 3
Alternative Methods for Solving the Problem
While the additive inverse method is the most efficient and conceptually sound, let's explore alternative approaches to solving this problem:
-
Number Line Visualization: Imagine a number line. Start at -1. Subtracting -4 means moving four units to the right (since subtracting a negative is the same as adding a positive). This visually confirms the answer of 3.
-
Using a Calculator: Modern calculators readily handle negative numbers. Simply input "-1 - (-4)" and the calculator will output 3. While convenient, relying solely on calculators hinders the development of conceptual understanding.
The Importance of Parentheses
Parentheses play a crucial role in mathematical expressions. They dictate the order of operations and clarify the meaning of the expression. In "-1 - (-4)," the parentheses around -4 are essential. Without them, the expression would be interpreted as "-1 - 4," which would equal -5. The parentheses indicate that we are subtracting a negative number, not simply subtracting 4. This highlights the importance of precise notation in mathematics.
Common Misconceptions about Negative Numbers
Several common misconceptions surround operations with negative numbers. Addressing these helps solidify a strong understanding:
-
Double Negative Confusion: Many students struggle with the concept of a double negative. Remember, subtracting a negative is equivalent to adding a positive. The double negative essentially cancels itself out.
-
Subtraction as Taking Away: While subtraction is often introduced as "taking away," this interpretation can be misleading when dealing with negative numbers. The additive inverse method provides a more robust and universally applicable approach.
-
Ignoring the Signs: A frequent error is ignoring the signs of the numbers involved. Always pay close attention to the signs (positive or negative) when performing any arithmetic operation involving integers.
Expanding the Concept: More Complex Examples
The principles applied to "-1 - (-4)" extend to more complex problems involving multiple negative numbers and different operations. For instance, consider:
-5 - (-2) + (-3) - 6
Following the order of operations (PEMDAS/BODMAS), and applying the additive inverse rule:
-5 + 2 + (-3) - 6 = -5 + 2 - 3 - 6 = -12
Similarly, consider:
(-2) * (-3) - (-5)
Here we have both multiplication and subtraction. Following PEMDAS/BODMAS:
(-2) * (-3) = 6
Then:
6 - (-5) = 6 + 5 = 11
Real-World Applications of Integer Subtraction
Integer subtraction isn't just an abstract mathematical concept. It has practical applications in various fields:
-
Finance: Calculating profit and loss, tracking bank balances, and managing debts all involve integer subtraction (for example, calculating the difference between income and expenses).
-
Temperature: Determining the temperature difference between two readings (e.g., the difference between -5°C and 10°C) involves integer subtraction.
-
Altitude: Calculating the difference in altitude between two points (e.g., the difference between sea level (0m) and a mountain peak at 2000m below sea level (-2000m) uses integer subtraction.
-
Computer Science: Integer arithmetic is fundamental to computer programming, influencing everything from game development to complex scientific simulations.
-
Physics: Many physical phenomena involve the concept of vectors, which are represented by integers or real numbers with direction, requiring calculations with negative numbers.
Frequently Asked Questions (FAQ)
-
Q: Why is subtracting a negative number the same as adding a positive number?
- A: Subtraction is the inverse operation of addition. Subtracting a negative number is equivalent to adding its additive inverse, which is a positive number. This is a fundamental property of arithmetic operations.
-
Q: What if I have more than two negative numbers being subtracted?
- A: Apply the additive inverse rule to each negative number sequentially. Then, perform the addition according to the order of operations.
-
Q: Can I use a different method besides the additive inverse method?
- A: While the number line visualization and calculators are helpful tools, the additive inverse method offers the most robust and conceptually sound understanding of integer subtraction.
-
Q: What are the practical implications of misunderstanding integer subtraction?
- A: Misunderstanding integer subtraction can lead to errors in various real-world applications, ranging from financial calculations to scientific computations, causing potentially significant consequences.
Conclusion: Mastering Integer Subtraction
Understanding integer subtraction, especially when dealing with negative numbers, is a cornerstone of mathematical literacy. The key lies in understanding the concept of additive inverses and applying the rule "a - b = a + (-b)." This article has provided a detailed explanation of the solution to "-1 - (-4)," explored alternative methods, addressed common misconceptions, and highlighted the real-world significance of this seemingly simple mathematical operation. By grasping these principles, you'll be well-equipped to tackle more complex arithmetic problems and strengthen your foundation in mathematics. Remember to practice regularly and don’t hesitate to use visual aids like the number line to reinforce your understanding. Consistent practice is the key to mastering this fundamental mathematical concept and building confidence in your abilities.
Latest Posts
Latest Posts
-
Is 3 Greater Than 2
Sep 19, 2025
-
Picture Of A Line Plot
Sep 19, 2025
-
Silk Road Ap World History
Sep 19, 2025
-
Examples Of Density Independent Limiting Factors
Sep 19, 2025
-
Convert 60 Degrees To Radians
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Negative 1 Minus Negative 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.