Negative 1 Minus Negative 5
zacarellano
Sep 19, 2025 · 5 min read
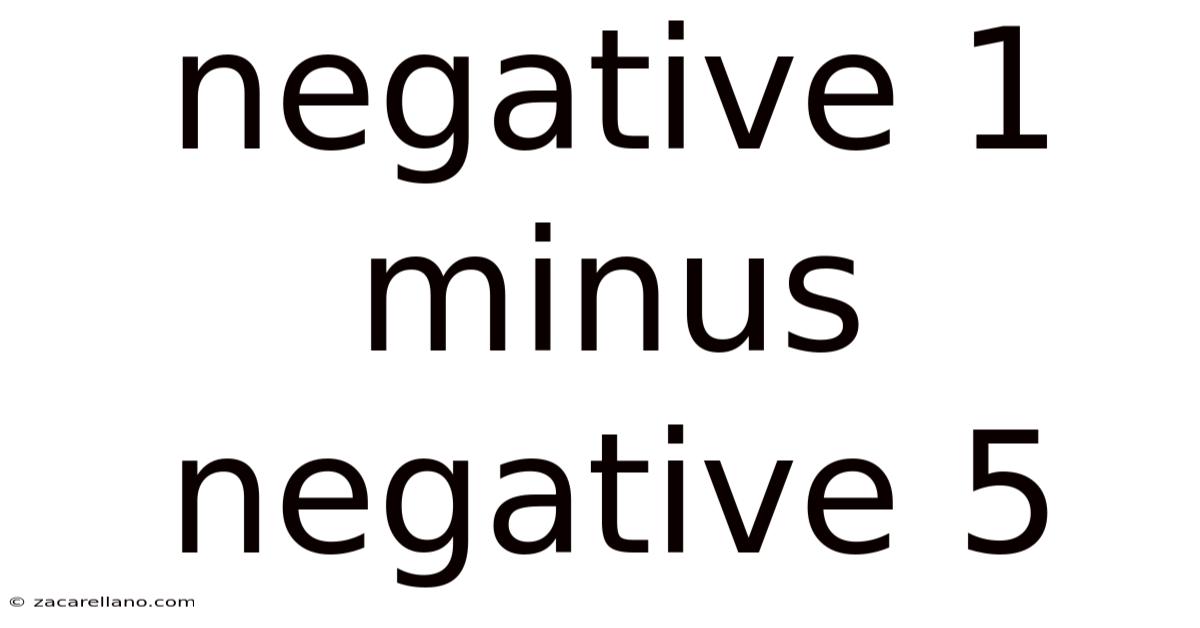
Table of Contents
Decoding the Mystery: Negative One Minus Negative Five
Understanding negative numbers can feel like navigating a tricky maze, especially when subtraction enters the picture. This comprehensive guide will illuminate the path to solving problems like "-1 - (-5)," explaining not only the solution but also the underlying mathematical principles and providing a robust understanding of negative number operations. We'll explore various approaches, address common misconceptions, and equip you with the confidence to tackle similar problems independently.
Introduction: Navigating the World of Negative Numbers
Negative numbers represent values less than zero. They are essential in various fields, from accounting (representing debt) to physics (representing temperature below zero). Mastering operations with negative numbers, including subtraction, is crucial for success in mathematics and beyond. This article focuses on the seemingly complex calculation: -1 - (-5). We will demystify the process, showing you how to arrive at the correct answer and, more importantly, why that answer is correct. By the end, you'll not just know the answer but also understand the underlying mathematical reasoning.
Understanding Subtraction: The "Adding the Opposite" Method
Subtraction can be conceptually understood as the addition of the opposite. This concept simplifies operations involving negative numbers significantly. Instead of directly subtracting a negative number, we transform the subtraction into an addition problem by changing the sign of the subtracted number.
Let's break down "-1 - (-5)" using this method:
-
Identify the subtraction: We have "-1 - (-5)."
-
Rewrite as addition: Subtracting a negative number is equivalent to adding its positive counterpart. Therefore, "-1 - (-5)" becomes "-1 + 5."
-
Solve the addition: Now we have a simple addition problem: -1 + 5. Think of it as starting at -1 on a number line and moving 5 units to the right (positive direction). This leads us to the answer: 4.
Therefore, -1 - (-5) = 4
Visualizing with a Number Line
A number line is a powerful tool for visualizing operations with negative numbers. Let's use it to illustrate -1 - (-5):
-
Start at -1: Place a marker at -1 on the number line.
-
Subtracting a negative: Subtracting a negative number is the same as moving to the right on the number line. Think of it as "undoing" the negativity.
-
Move 5 units right: Since we are subtracting -5, we move 5 units to the right from our starting point (-1).
-
Arrive at 4: This movement lands us at the number 4 on the number line.
This visual representation confirms that -1 - (-5) = 4.
The Importance of Parentheses
Parentheses are crucial in mathematical expressions. They establish the order of operations and help avoid ambiguity. In our example, "-1 - (-5)," the parentheses around "-5" are essential. They indicate that the entire -5 is being subtracted, not just the 5. If the parentheses were omitted, we would have "-1 - 5," which is a completely different calculation resulting in -6. Always pay close attention to parentheses when working with negative numbers.
Expanding the Understanding: Different Perspectives
While the "adding the opposite" method is efficient and widely used, let's explore other approaches to reinforce understanding.
Debt and Credits Analogy
Imagine you have a debt of $1 (-$1). Then someone removes a debt of $5 (-$5) from you. In essence, they are giving you $5. Your net position moves from owing $1 to having $4. This real-world scenario mirrors the mathematical operation, highlighting the intuitive meaning behind subtracting a negative number.
Temperature Changes
Consider a scenario where the temperature is -1°C. Then, the temperature increases by 5°C. The change is represented as -1 - (-5) because we are subtracting a negative change (a decrease). The final temperature is 4°C. This example uses a concrete context to illustrate the mathematical operation.
Addressing Common Misconceptions
Many students struggle with negative numbers, leading to frequent mistakes. Let's address some common misconceptions:
-
Two negatives don't always make a positive: This statement is true only in the context of multiplication or division. In addition and subtraction, the rules are different. Subtracting a negative is equivalent to adding a positive; adding a negative is subtracting a positive.
-
Ignoring parentheses: Ignoring parentheses can drastically alter the result. Always carefully consider the order of operations and the meaning of the parentheses.
-
Confusing signs: The sign of a number indicates its direction (positive or negative), while the operation sign (+ or -) dictates the action to be performed (addition or subtraction). Keeping these distinct is essential for accuracy.
Further Practice and Exploration
To solidify your understanding, try solving similar problems:
- -3 - (-7)
- -10 - (-2)
- 5 - (-4)
- -2 - (-2)
Remember to use the "adding the opposite" method, visualize with a number line, and carefully consider the role of parentheses. Experiment with different scenarios using the debt/credit or temperature analogies to reinforce your comprehension.
Frequently Asked Questions (FAQ)
Q1: Why does subtracting a negative number result in addition?
A1: Subtraction is the inverse of addition. Subtracting a negative number is like "undoing" the subtraction of a positive number. This "undoing" action translates to adding the positive equivalent.
Q2: Can I always rewrite subtraction problems involving negatives as addition problems?
A2: Yes, this is a fundamental principle in working with negative numbers. Rewriting subtraction as addition simplifies the calculation and reduces the chance of errors.
Q3: What happens if I subtract a positive number from a negative number?
A3: In this case, you are essentially moving further into the negative territory on the number line. For example, -2 - 3 = -5.
Q4: Are there other methods to solve problems involving negative numbers besides the number line and “adding the opposite”?
A4: While the number line and the "adding the opposite" method are highly effective and widely used, you can also use other strategies like visualizing chips (representing positive and negative values) or employing algebraic manipulation techniques as your mathematical skills advance.
Conclusion: Mastering Negative Number Subtraction
Understanding and mastering operations involving negative numbers is fundamental to building a strong foundation in mathematics. This article has provided a detailed explanation of how to solve -1 - (-5), demonstrating multiple approaches and addressing common misconceptions. Remember the key takeaway: subtracting a negative is the same as adding a positive. By consistently applying the principles and practicing regularly, you'll develop a strong grasp of negative number arithmetic and confidently navigate more complex mathematical problems in the future. The seemingly challenging problem of "-1 - (-5)" becomes straightforward with a clear understanding of the underlying concepts and methods explained here. Now, go forth and conquer the world of negative numbers!
Latest Posts
Latest Posts
-
Location Of Dna In Prokaryotes
Sep 19, 2025
-
Long Run Perfect Competition Graph
Sep 19, 2025
-
Quantos Centavos Tem Um Real
Sep 19, 2025
-
Factors That Influence Membrane Fluidity
Sep 19, 2025
-
Whats The Function Of Mrna
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Negative 1 Minus Negative 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.