Negative 2 Divided By 4
zacarellano
Sep 14, 2025 · 5 min read
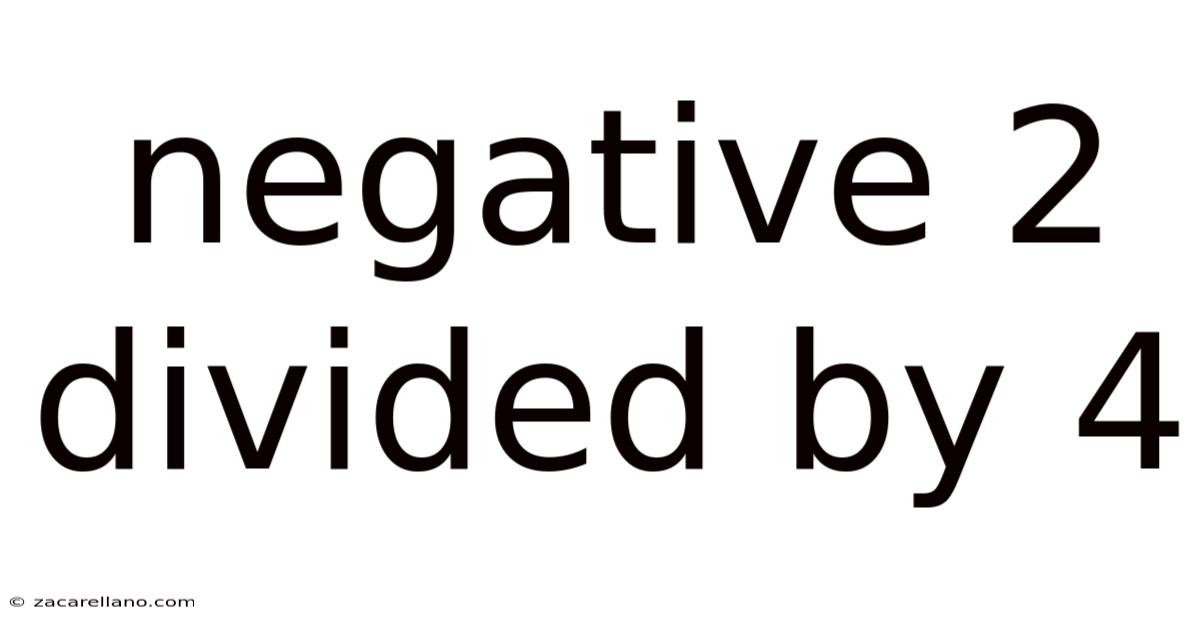
Table of Contents
Unpacking -2 ÷ 4: A Deep Dive into Negative Division
Understanding division, especially when negative numbers are involved, can seem daunting at first. This article will provide a comprehensive explanation of the calculation -2 ÷ 4, exploring the process, the underlying mathematical principles, and addressing common misconceptions. We'll delve into why the answer is what it is, exploring practical applications and building a strong foundational understanding of this concept. This will be helpful for students learning about arithmetic operations, as well as anyone looking to refresh their understanding of basic math.
Understanding Division: A Quick Refresher
Before tackling negative numbers, let's revisit the fundamental concept of division. Division is essentially the inverse operation of multiplication. When we say 6 ÷ 2 = 3, we're asking: "What number, when multiplied by 2, gives us 6?" The answer, of course, is 3. Division helps us to split a quantity into equal parts.
Think of it practically: if you have 6 cookies and want to share them equally among 2 friends, each friend gets 3 cookies. This simple example highlights the core idea behind division: splitting a whole into equal parts.
Introducing Negative Numbers: The Sign Rules
Now, let's introduce the complication of negative numbers. When dealing with negative numbers in division, the rules concerning the sign of the result are crucial. These rules stem from the properties of multiplication and the relationship between division and multiplication. The fundamental rule is:
-
When dividing two numbers with different signs (one positive, one negative), the result is always negative.
-
When dividing two numbers with the same sign (both positive or both negative), the result is always positive.
Calculating -2 ÷ 4: A Step-by-Step Approach
Now, let's address the specific problem: -2 ÷ 4. Following the rules of division and the sign rules for negative numbers, we can break down the calculation:
-
Ignore the signs initially: Consider the absolute values of the numbers: 2 and 4.
-
Perform the division: 2 ÷ 4 = 0.5 (or 1/2 as a fraction).
-
Apply the sign rule: Since we are dividing a negative number (-2) by a positive number (4), the result will be negative.
-
Final Answer: Therefore, -2 ÷ 4 = -0.5 (or -1/2).
Visualizing the Division: A Geometrical Interpretation
We can visualize division using a number line. Imagine the number line representing quantities. To divide -2 by 4, we are essentially asking, "How many times can we fit 4 into -2?" The answer is not a whole number. We are dividing a smaller negative quantity by a larger positive quantity. It's like trying to distribute -2 units of something into 4 equal parts. This results in each part having -0.5 units.
Practical Applications: Real-World Examples
Negative numbers often represent decreases, losses, or debts in real-world scenarios. Consider these examples:
-
Temperature change: If the temperature drops 2 degrees over 4 hours, the average hourly temperature change is -0.5 degrees per hour. This illustrates -2 ÷ 4 = -0.5 in a real-world context.
-
Financial losses: If a company loses $2 million over 4 quarters, its average quarterly loss is -$0.5 million. Again, this showcases the practical application of this division problem.
-
Debt repayment: If you owe $2 and you pay it off in 4 equal installments, each installment is -$0.5. The negative sign indicates a reduction in your debt.
Addressing Common Misconceptions
Several misconceptions often arise when dealing with negative numbers and division. Let's clarify these common errors:
-
Ignoring the negative sign: Many students make the mistake of simply calculating 2 ÷ 4 = 0.5 and ignoring the negative sign. It's crucial to remember that the negative sign is an integral part of the number and must be considered in the operation.
-
Reversing the signs: Some students might incorrectly assume that the result will be positive because they are dividing a smaller number by a larger number. However, the sign rules depend solely on the signs of the numbers involved, not their magnitudes.
-
Confusing division with subtraction: Division and subtraction are distinct operations. Subtraction involves finding the difference between two numbers, while division involves splitting a quantity into equal parts.
Further Exploration: Extending the Concept
Understanding -2 ÷ 4 lays the groundwork for more advanced concepts. Here are some extensions of this basic principle:
-
Dividing by fractions: Dividing by a fraction involves multiplying by its reciprocal. For example, -2 ÷ (1/4) = -2 * 4 = -8.
-
Dividing by zero: It's crucial to understand that division by zero is undefined in mathematics. Attempting to divide any number by zero will result in an error.
-
Complex numbers: As you advance in mathematics, you'll encounter complex numbers, which include both real and imaginary parts. The principles of division still apply, though the process becomes slightly more intricate.
Frequently Asked Questions (FAQs)
Q1: Why is the result negative?
A1: The result is negative because we are dividing a negative number (-2) by a positive number (4). The rules of division with signed numbers dictate that when dividing numbers with different signs, the result is always negative.
Q2: What if the numbers were reversed (4 ÷ -2)?
A2: If the numbers were reversed (4 ÷ -2), the result would still be -2. This is because we are now dividing a positive number (4) by a negative number (-2), again resulting in a negative quotient according to the sign rules.
Q3: Can I use a calculator to solve this?
A3: Yes, most calculators will correctly compute -2 ÷ 4 = -0.5. However, it's essential to understand the underlying mathematical principles behind the calculation to avoid making errors in more complex problems.
Q4: How does this relate to fractions?
A4: The result -0.5 is equivalent to the fraction -1/2. Understanding the relationship between decimals and fractions is crucial for mastering arithmetic operations.
Conclusion: Mastering Negative Division
Mastering the division of negative numbers is a foundational step in developing a strong mathematical understanding. The calculation -2 ÷ 4 = -0.5 might seem simple, but understanding the underlying principles – including the sign rules and the geometrical interpretation – is crucial for tackling more complex problems. By understanding these principles, you'll build a solid foundation for further mathematical exploration, confidently handling negative numbers in various contexts. Remember, practice is key to solidifying your understanding. Work through several similar problems, and you'll quickly become proficient in dividing negative numbers. Don't hesitate to revisit this explanation and use the examples provided to reinforce your learning.
Latest Posts
Latest Posts
-
What Is Binding Price Floor
Sep 14, 2025
-
Standard Enthalpy Of Formation Chart
Sep 14, 2025
-
Addition Of Decimals Word Problems
Sep 14, 2025
-
Ap Statistics Unit 4 Review
Sep 14, 2025
-
Ap Microeconomics Unit 1 Test
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Negative 2 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.