Negative 3 Minus Negative 6
zacarellano
Sep 23, 2025 · 6 min read
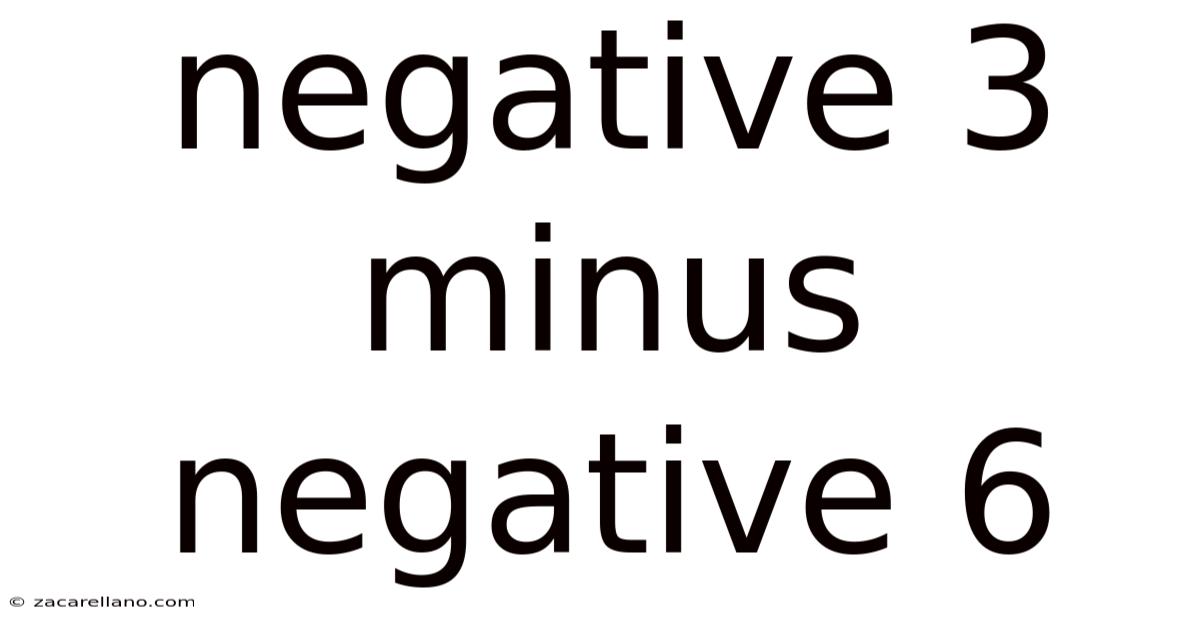
Table of Contents
Decoding the Mystery: Negative 3 Minus Negative 6
Understanding negative numbers can be a hurdle for many, but mastering them unlocks a whole new world of mathematical possibilities. This article dives deep into the seemingly simple problem of "-3 - (-6)," explaining not only the solution but also the underlying principles and broader applications of subtracting negative numbers. By the end, you'll not only know the answer but also possess a confident grasp of this fundamental concept.
Introduction: Navigating the World of Negative Numbers
Negative numbers represent values less than zero. They're essential in various fields, from accounting (representing debts) to physics (describing temperature below zero). Understanding operations involving negative numbers, particularly subtraction, is crucial for success in mathematics and beyond. This article focuses on clarifying the seemingly confusing operation of subtracting a negative number, using "-3 - (-6)" as our central example. We'll break down the process step-by-step, explore the underlying mathematical rules, and even address some common misconceptions.
Understanding Subtraction: The "Take Away" and "Difference" Perspectives
Before tackling negative numbers, let's briefly revisit the concept of subtraction. Subtraction can be viewed in two ways:
- "Take Away": This is the most intuitive approach. If you have 5 apples and take away 2, you're left with 3 (5 - 2 = 3).
- "Difference": This approach focuses on finding the difference between two numbers. The difference between 8 and 3 is 5 (8 - 3 = 5). This perspective is crucial when dealing with negative numbers.
The Crucial Rule: Subtracting a Negative is Adding a Positive
The core concept to grasp is this: subtracting a negative number is equivalent to adding its positive counterpart. This seemingly counter-intuitive rule stems from the properties of negative numbers and the definition of subtraction as the inverse of addition.
Let's illustrate this with our example: -3 - (-6).
Following the rule, we can rewrite the equation as: -3 + 6.
This transformation simplifies the problem significantly. Now, we're dealing with a simple addition problem involving a negative and a positive number.
Solving -3 + 6: Visualizing the Solution
We can visualize this addition on a number line. Start at -3. Adding 6 means moving 6 units to the right (positive direction) on the number line. This brings us to the number 3.
Therefore, -3 + 6 = 3. Consequently, -3 - (-6) = 3.
The Number Line: A Powerful Tool for Understanding
The number line is an invaluable tool for visualizing operations with negative numbers. It provides a clear, visual representation of the movement involved in addition and subtraction.
- Adding a positive number: Move to the right on the number line.
- Adding a negative number: Move to the left on the number line.
- Subtracting a positive number: Move to the left on the number line.
- Subtracting a negative number: Move to the right on the number line.
By using the number line, you can visually track the changes in value and gain a deeper understanding of the operations involved.
A Deeper Dive: The Mathematical Explanation
The rule "subtracting a negative is adding a positive" is grounded in the mathematical concept of additive inverses. Every number has an additive inverse, a number that, when added to it, results in zero. The additive inverse of a number is simply its opposite.
- The additive inverse of 5 is -5 (5 + (-5) = 0).
- The additive inverse of -3 is 3 (-3 + 3 = 0).
Subtraction can be defined as adding the additive inverse. So, a - b is equivalent to a + (-b).
Applying this to our example:
-3 - (-6) = -3 + (the additive inverse of -6) = -3 + 6 = 3.
This demonstrates the mathematical foundation behind the seemingly simple rule.
Expanding the Concept: More Complex Examples
Let's explore more complex examples to solidify your understanding:
- -8 - (-12): This becomes -8 + 12 = 4.
- -5 - (-5): This becomes -5 + 5 = 0.
- 10 - (-3): This becomes 10 + 3 = 13.
- -2 - (+4): Remember that subtracting a positive is the same as adding a negative. So, this becomes -2 + (-4) = -6.
These examples showcase the consistent application of the fundamental rule: subtracting a negative is equivalent to adding a positive.
Addressing Common Misconceptions
Several common misconceptions surround subtracting negative numbers. Let's address some of them:
- Thinking subtracting always means a smaller result: This is true for positive numbers, but not always for negative numbers. Subtracting a negative number can actually increase the value.
- Confusing signs: Carefully track the signs. A common mistake is to incorrectly interpret the signs, leading to an incorrect result. Always pay close attention to whether you're adding or subtracting a positive or a negative number.
- Ignoring the parentheses: Parentheses are crucial in indicating the order of operations. Ignoring them can lead to errors in calculations.
Real-World Applications: Where Negative Numbers Matter
Negative numbers and the ability to perform operations with them are not just abstract mathematical concepts. They have numerous practical applications:
- Finance: Representing debt, losses, or negative cash flow.
- Temperature: Measuring temperatures below zero degrees Celsius or Fahrenheit.
- Elevation: Describing locations below sea level.
- Physics: Representing negative velocity or acceleration.
- Computer Science: Representing negative values in data structures and algorithms.
Frequently Asked Questions (FAQ)
Q: Why is subtracting a negative the same as adding a positive?
A: It stems from the definition of subtraction as adding the additive inverse (opposite) of a number. Subtracting a negative is equivalent to adding its positive counterpart because they are additive inverses.
Q: Can I always rewrite subtraction as addition?
A: Yes, you can always rewrite subtraction as adding the additive inverse. This is a powerful technique for simplifying calculations involving negative numbers.
Q: What if I have multiple negatives in a problem?
A: Work through the subtraction operations one at a time, applying the rule "subtracting a negative is adding a positive" each time. Take it step-by-step, and you’ll arrive at the correct answer.
Q: Are there any shortcuts for solving these problems?
A: Yes! Once you're comfortable with the concept, you can often mentally transform the expression into an addition problem and solve it directly. Practice is key to developing this skill.
Conclusion: Mastering Negative Number Subtraction
Mastering subtraction with negative numbers is a significant step in developing a solid foundation in mathematics. By understanding the underlying principles—the concept of additive inverses, the equivalence of subtracting a negative to adding a positive, and the visual aid of the number line—you can confidently tackle any problem involving negative numbers. Remember, consistent practice and attention to detail are essential to building proficiency. The seemingly simple "-3 - (-6)" problem opens the door to a deeper understanding of the rich and versatile world of mathematics. Continue practicing, explore further applications, and enjoy the journey of mathematical discovery!
Latest Posts
Latest Posts
-
Centre Of Mass Of Hemisphere
Sep 23, 2025
-
Diagram Of The Eye Psychology
Sep 23, 2025
-
Electric Field And Potential Relation
Sep 23, 2025
-
How To Add Subtract Integers
Sep 23, 2025
-
Factoring The Perfect Square Trinomial
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Negative 3 Minus Negative 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.