Negative 3 Times Negative 1
zacarellano
Sep 08, 2025 · 6 min read
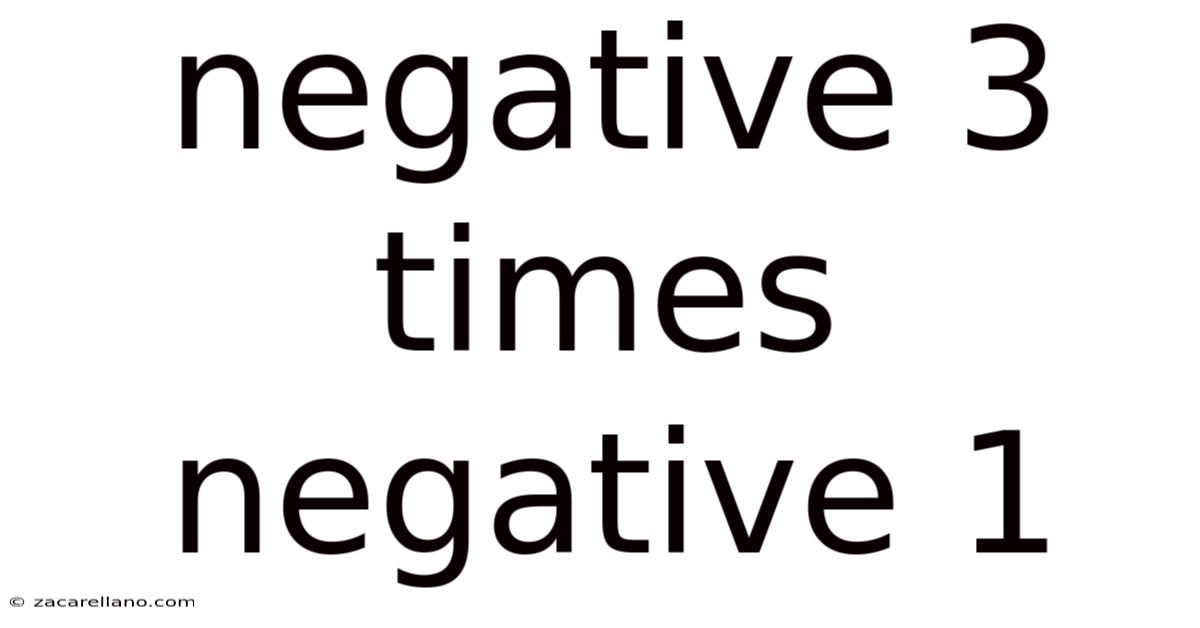
Table of Contents
Delving into the Depths: Why Negative 3 Multiplied by Negative 1 Equals Positive 3
Understanding the multiplication of negative numbers can be a stumbling block for many, even those comfortable with basic arithmetic. This article will explore the seemingly counter-intuitive concept of why a negative number multiplied by another negative number results in a positive number. Specifically, we'll delve deep into the calculation of -3 x -1 = 3, explaining the underlying principles, providing visual representations, and addressing frequently asked questions. By the end, you'll not only know the answer but also grasp the mathematical reasoning behind it.
Introduction: The Mystery of Negative Numbers
Negative numbers represent values less than zero. They extend the number line beyond zero in the opposite direction of positive numbers. While adding and subtracting negative numbers might feel relatively straightforward, multiplication and division introduce a new layer of complexity. The question of "why negative times negative equals positive" is a common one, and the answer goes beyond simple rote memorization; it’s rooted in the consistent application of mathematical rules. This article aims to demystify this fundamental concept.
Understanding the Number Line and Opposites
Before we tackle multiplication, let's refresh our understanding of the number line. The number line visually represents numbers, extending infinitely in both positive and negative directions. Zero sits in the middle, acting as a dividing point. Each number has its opposite, located on the other side of zero and equidistant from it. For instance, the opposite of 3 is -3, and the opposite of -5 is 5. This concept of opposites is crucial to understanding the multiplication of negative numbers.
Visualizing Multiplication as Repeated Addition
One way to visualize multiplication is through repeated addition. For example, 3 x 4 can be thought of as adding 3 four times: 3 + 3 + 3 + 3 = 12. This approach helps us understand the impact of negative numbers in multiplication.
Let's consider -3 x 2. Using repeated addition, this would be: (-3) + (-3) = -6. Here, we're adding -3 twice, resulting in a more negative value. The negative sign indicates a direction on the number line – moving towards the left from zero.
The Pattern Emerges: Exploring Multiple Scenarios
Now let's observe a pattern by systematically changing the signs:
- 3 x 2 = 6: A positive number multiplied by a positive number equals a positive number.
- 3 x -2 = -6: A positive number multiplied by a negative number equals a negative number.
- -3 x 2 = -6: A negative number multiplied by a positive number equals a negative number.
- -3 x -2 = 6: A negative number multiplied by a negative number equals a positive number.
Notice the pattern: when the signs are different (one positive, one negative), the result is negative. When the signs are the same (both positive or both negative), the result is positive. This consistent pattern underlies the rule that negative times negative equals positive.
The Distributive Property: A Formal Mathematical Justification
A more rigorous mathematical justification lies in the distributive property of multiplication. This property states that for any numbers a, b, and c: a(b + c) = ab + ac. Let's apply this property to demonstrate why -3 x -1 = 3:
We know that: 0 = 3 x 0
We can rewrite 0 as (1 + (-1)): 0 = 3 x (1 + (-1))
Now, using the distributive property: 3 x (1 + (-1)) = 3 x 1 + 3 x (-1) = 3 + (-3) = 0
This equation holds true. Now let's consider a similar equation, replacing 3 with -3:
0 = -3 x (1 + (-1))
Applying the distributive property: -3 x (1 + (-1)) = -3 x 1 + (-3) x (-1) = -3 + (-3) x (-1)
Since the entire expression equals zero, and we already have -3, the remaining term (-3) x (-1) must equal 3 to maintain the balance. Therefore, (-3) x (-1) = 3.
The Concept of Inverse Operations
Another way to view the multiplication of negative numbers is through the concept of inverse operations. Multiplication and division are inverse operations; they undo each other. Similarly, addition and subtraction are inverse operations.
Consider the equation: 3 x (-1) = -3. If we divide both sides by -1, we get: 3 = -3 / -1. Dividing a negative number by another negative number results in a positive number, reinforcing the principle we've been exploring.
Beyond -3 x -1: Generalizing the Rule
The principle demonstrated with -3 x -1 applies universally to the multiplication of any two negative numbers. The product of two negative numbers will always be positive. This rule is fundamental to more advanced mathematical concepts and is essential for understanding algebra, calculus, and other branches of mathematics.
Addressing Common Misconceptions
- It "just is": While memorizing the rule is helpful for quick calculations, understanding the underlying mathematical principles provides a deeper, more robust understanding.
- It's arbitrary: The rule isn't arbitrary; it's a logical consequence of maintaining consistency within the number system and its operations.
- It's too complex: With the explanations provided, the concept becomes far more accessible and less intimidating.
Frequently Asked Questions (FAQ)
- Q: Why isn't negative times negative equal to negative? A: This would violate the consistent application of mathematical rules, specifically the distributive property and the concept of inverse operations. Maintaining consistency within the mathematical system requires negative times negative to equal positive.
- Q: Does this rule apply to all negative numbers? A: Yes, the rule applies to the multiplication of any two negative numbers, regardless of their magnitude.
- Q: How can I explain this to a child? A: Use visual aids like the number line and the concept of repeated addition. Explain it in simple terms, focusing on the pattern that emerges when multiplying numbers with different and same signs. Avoid overly technical jargon.
- Q: Are there any real-world applications of this concept? A: The principles governing negative number multiplication are fundamental to various fields, including physics (velocity and acceleration calculations), finance (calculating losses and profits), and computer programming (handling negative values).
Conclusion: Mastering the Fundamentals
Understanding why negative 3 multiplied by negative 1 equals positive 3 is crucial for building a solid foundation in mathematics. It's not merely about memorizing a rule; it’s about grasping the underlying mathematical principles that govern the behavior of negative numbers. By exploring different approaches, including visual representations, the distributive property, and the concept of inverse operations, we've demonstrated the logical consistency and inherent reason behind this seemingly paradoxical rule. This understanding will serve you well as you progress to more advanced mathematical concepts. Remember, mathematics is not about memorization alone; it is about understanding the logic and beauty of the system itself.
Latest Posts
Latest Posts
-
Ap World Unit 7 Test
Sep 09, 2025
-
Practice Saq Ap World History
Sep 09, 2025
-
Lcm For 15 And 25
Sep 09, 2025
-
Algebra 2 Equations And Answers
Sep 09, 2025
-
Triangle With Two Right Angles
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Negative 3 Times Negative 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.