Negative 3 Times Negative 3
zacarellano
Sep 11, 2025 · 6 min read
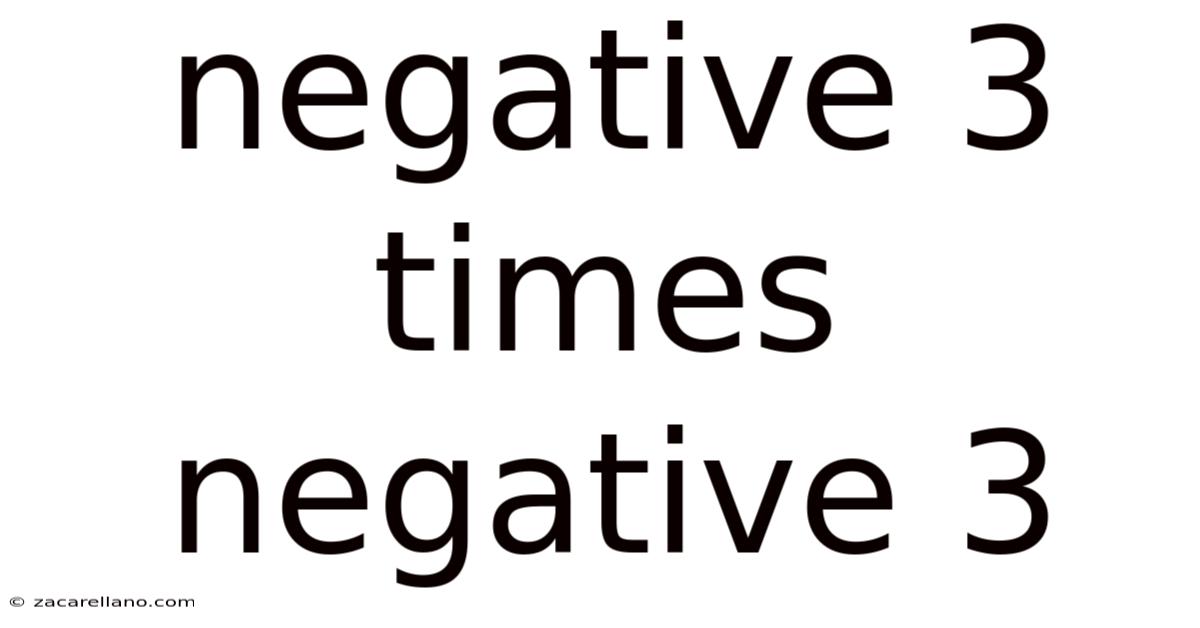
Table of Contents
Unraveling the Mystery: Negative 3 Times Negative 3
Understanding multiplication involving negative numbers can be tricky. Many students struggle with the concept, especially when confronted with a problem like "-3 x -3". This article aims to demystify this seemingly complex calculation, providing a comprehensive explanation that goes beyond a simple answer. We'll explore the rules of multiplication with negative numbers, delve into the underlying mathematical principles, and offer practical examples to solidify your understanding. By the end, you'll not only know that -3 x -3 = 9, but also why this is the case.
Understanding the Fundamentals: Multiplication and Negative Numbers
Before diving into the specifics of -3 x -3, let's establish a foundation. Multiplication, at its core, is repeated addition. For example, 3 x 4 means adding 3 four times: 3 + 3 + 3 + 3 = 12. This simple concept extends to negative numbers.
Now, let's consider what happens when we introduce negative numbers into the equation. Understanding the multiplication of negative numbers requires grasping the concept of opposites or inverses. The opposite of a positive number is a negative number, and vice-versa. This is crucial for grasping the rules surrounding multiplication with negative signs.
-
Positive x Positive: This is the simplest scenario. A positive number multiplied by a positive number always results in a positive number. For example, 3 x 4 = 12.
-
Positive x Negative: When a positive number is multiplied by a negative number, the result is always negative. For example, 3 x -4 = -12. Think of it as repeatedly adding -4 three times: -4 + (-4) + (-4) = -12.
-
Negative x Positive: Similar to the above, a negative number multiplied by a positive number yields a negative result. For example, -3 x 4 = -12. This can be interpreted as repeatedly subtracting 3 four times, or adding -3 four times.
-
Negative x Negative: This is where the seeming complexity lies. A negative number multiplied by a negative number results in a positive number. This is the rule that governs our core problem: -3 x -3 = 9. We'll explore why this is true in the next section.
The Mathematical Justification: Why Negative Times Negative Equals Positive
There are several ways to explain why a negative multiplied by a negative equals a positive. Let's explore a couple of approaches:
1. The Pattern Approach: Observe the patterns in the following multiplications:
- 3 x 3 = 9
- 3 x 2 = 6
- 3 x 1 = 3
- 3 x 0 = 0
- 3 x -1 = -3
- 3 x -2 = -6
- 3 x -3 = -9
Notice that as the second factor decreases by 1, the product decreases by 3. Continuing this pattern:
- 3 x -4 = -12
- 3 x -5 = -15
Now, let's look at it from the perspective of multiplying by -3:
- -3 x 3 = -9
- -3 x 2 = -6
- -3 x 1 = -3
- -3 x 0 = 0
Following the pattern, as the second factor decreases by 1, the product increases by 3:
- -3 x -1 = 3
- -3 x -2 = 6
- -3 x -3 = 9
2. The Distributive Property Approach: The distributive property states that a(b + c) = ab + ac. Let's use this to illustrate why (-1) x (-1) = 1:
We know that 1 + (-1) = 0. Let's multiply both sides of this equation by -1:
-1 x (1 + (-1)) = -1 x 0
This simplifies to:
-1 x 1 + (-1) x (-1) = 0
We know that -1 x 1 = -1, so we have:
-1 + (-1) x (-1) = 0
To solve for (-1) x (-1), we add 1 to both sides:
(-1) x (-1) = 1
3. The Number Line Approach: Imagine a number line. Multiplication can be visualized as movement along the line. A positive multiplier indicates movement in the positive direction, while a negative multiplier indicates movement in the negative direction.
- 3 x 3: Start at 0, move 3 units to the right (positive) three times. You end up at 9.
- 3 x -3: Start at 0, move 3 units to the left (negative) three times. You end up at -9.
- -3 x 3: Start at 0, move 3 units to the left (negative) three times. You end up at -9.
- -3 x -3: Start at 0, move 3 units to the right (positive) three times (because the negative times negative reverses the direction). You end up at 9.
Practical Applications and Examples
The concept of multiplying negative numbers has widespread applications in various fields, including:
-
Finance: Calculating losses or debts. A loss of $3 per day for 3 days results in a total loss of -$9, represented as -3 x 3 = -9. But if you avoid a loss of $3 per day for 3 days, you gain $9, represented as -3 x -3 = 9.
-
Physics: Dealing with vectors and forces. Negative signs often represent direction (e.g., negative velocity indicates movement in the opposite direction).
-
Programming: Many programming languages use negative numbers for various calculations and data manipulation.
Here are a few more examples:
- -5 x -2 = 10
- -10 x -10 = 100
- -1/2 x -2 = 1
- -0.5 x -4 = 2
Frequently Asked Questions (FAQ)
-
Q: Why can't we just say that negative times negative is always negative?
- A: This is incorrect and contradicts the consistent mathematical patterns and properties we've explored. If we followed this rule, the mathematical system would become inconsistent and break fundamental properties like the distributive property.
-
Q: Is there any other way to understand this besides the patterns and the distributive property?
- A: Yes, you can use visual aids such as the number line approach or consider it in terms of reversing the direction of movement, as explained earlier.
-
Q: Does this rule apply to all types of numbers, including fractions and decimals?
- A: Yes, the rule that a negative number multiplied by a negative number results in a positive number applies to all real numbers, including fractions, decimals, and irrational numbers.
-
Q: Is there a simple mnemonic device to remember this rule?
- A: While there's no single universally accepted mnemonic, remembering that "negative times negative equals positive" is often sufficient. Understanding why it's true, however, is more helpful than simply memorizing.
Conclusion: Mastering Negative Number Multiplication
Understanding the multiplication of negative numbers, especially the concept of "-3 x -3 = 9", is fundamental to a strong grasp of mathematics. It's not simply about memorizing a rule; it's about understanding the underlying principles and patterns. By exploring the patterns, applying the distributive property, and visualizing the concept on a number line, you can build a solid foundation for working with negative numbers in more complex mathematical scenarios. The seemingly challenging concept of negative times negative becomes clear and logical when approached methodically. Mastering this concept will unlock a deeper understanding of algebra and beyond.
Latest Posts
Latest Posts
-
Why Was Andrew Jackson Bad
Sep 11, 2025
-
Prior Restraint Ap Gov Definition
Sep 11, 2025
-
Lcm Of 7 And 10
Sep 11, 2025
-
What Is A Runtime Error
Sep 11, 2025
-
State Function Vs Path Function
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Negative 3 Times Negative 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.