Negative 4 Minus Negative 4
zacarellano
Sep 13, 2025 · 5 min read
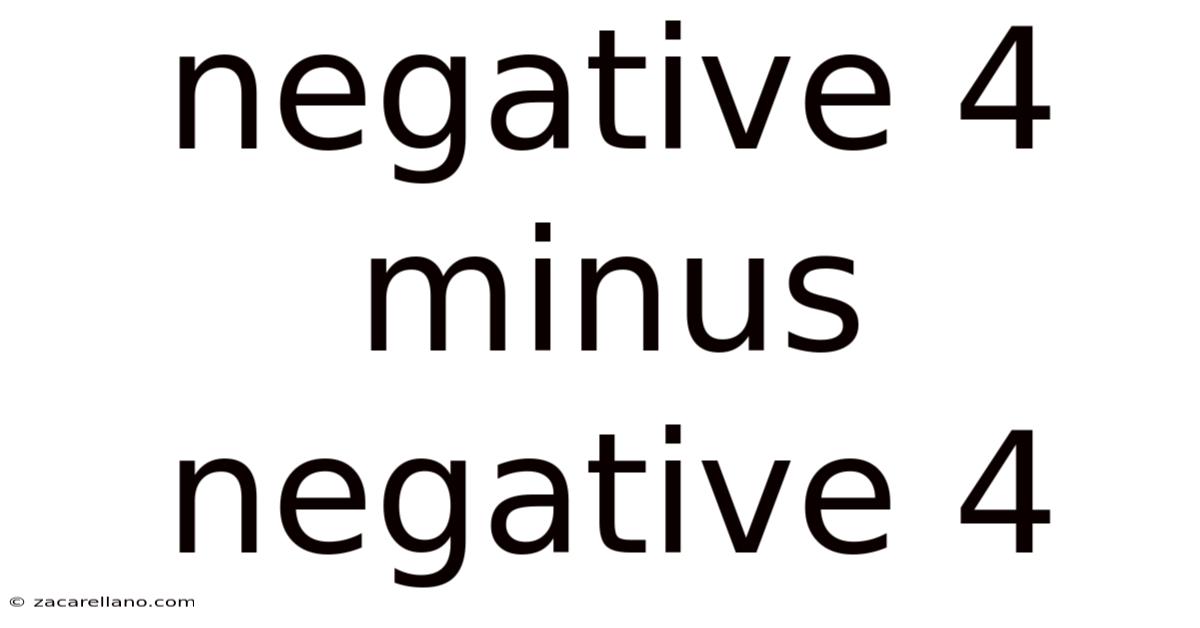
Table of Contents
Decoding the Mystery: Negative Four Minus Negative Four (-4 - (-4))
Understanding negative numbers can be tricky, especially when dealing with subtraction of negatives. This article will delve into the seemingly simple problem of negative four minus negative four (-4 - (-4)), providing a comprehensive explanation that goes beyond just the answer. We'll explore the underlying principles, different approaches to solving the problem, and address common misconceptions surrounding negative numbers and subtraction. This exploration will equip you with a solid understanding not just of this specific equation, but of negative number arithmetic in general.
Introduction: Navigating the World of Negative Numbers
Negative numbers represent values less than zero. They are crucial in various fields, from finance (representing debt) to physics (representing temperature below zero). Mastering their manipulation is essential for proficiency in mathematics and its applications. Subtraction, particularly when involving negative numbers, often presents a challenge. This article will clearly demonstrate how to approach and solve the equation -4 - (-4), clarifying the concepts and eliminating potential confusion.
Understanding Subtraction: The Concept of "Taking Away"
Before tackling the problem, let's review the fundamental concept of subtraction. Subtraction essentially means "taking away" or finding the difference between two numbers. For example, 5 - 2 means taking away 2 from 5, resulting in 3. This intuitive understanding forms the basis for our approach to subtracting negative numbers.
The Double Negative: A Key to Understanding -4 - (-4)
The core of this problem lies in understanding the double negative, represented by "-(-4)". In mathematics, two consecutive negative signs cancel each other out, resulting in a positive sign. Therefore, -(-4) is equivalent to +4 or simply 4. This simplification is the key to solving the entire equation.
Step-by-Step Solution: Breaking Down -4 - (-4)
Here's a step-by-step breakdown of how to solve -4 - (-4):
-
Rewrite the Equation: Start by rewriting the equation, focusing on the double negative: -4 - (-4)
-
Simplify the Double Negative: Replace "-(-4)" with "+4" or simply 4. This simplifies the equation to: -4 + 4
-
Perform the Addition: Now, we have a simple addition problem: -4 + 4. This represents adding a positive 4 to a negative 4.
-
The Result: Adding a number and its opposite (its additive inverse) always results in zero. Therefore, -4 + 4 = 0.
Thus, the solution to -4 - (-4) is 0.
Visual Representation: The Number Line Approach
Using a number line can provide a visual understanding of the operation.
-
Start at -4: Begin at the point representing -4 on the number line.
-
Subtract -4 (or add +4): Subtracting a negative number is the same as adding its positive counterpart. So, instead of moving to the left (which would represent subtracting a positive number), we move to the right by 4 units.
-
Arrive at 0: After moving 4 units to the right from -4, you arrive at 0 on the number line. This visually confirms that -4 - (-4) = 0.
The Additive Inverse: A Deeper Dive
The concept of the additive inverse plays a crucial role in understanding this equation and negative number arithmetic in general. The additive inverse of a number is the number that, when added to the original number, results in zero. For example:
- The additive inverse of 5 is -5 (because 5 + (-5) = 0)
- The additive inverse of -4 is 4 (because -4 + 4 = 0)
In our equation, -4 - (-4), we are essentially adding the additive inverse of -4 to -4, which, as explained, always results in zero.
Addressing Common Misconceptions
Many students struggle with subtraction of negative numbers. Some common misconceptions include:
-
Incorrectly applying the double negative: Some might mistakenly add the numbers without changing the sign of the second negative, leading to an incorrect answer of -8. Remember, the double negative translates to a positive.
-
Confusing subtraction with addition: Subtracting a negative number is NOT the same as simply subtracting a positive number. It's crucial to understand the rule of changing the sign of the second number and then adding.
-
Difficulty visualizing negative numbers: Using a number line or other visual aids can be immensely helpful in grasping the concept and visualizing the process.
Expanding the Concept: More Examples
Let's explore some similar problems to further solidify your understanding:
-
-5 - (-2): This simplifies to -5 + 2 = -3
-
-10 - (-10): This simplifies to -10 + 10 = 0
-
7 - (-3): This simplifies to 7 + 3 = 10
Notice the consistent pattern: subtracting a negative number is equivalent to adding its positive counterpart.
Real-World Applications: Where Negative Numbers Matter
Negative numbers are not just abstract mathematical concepts; they have practical applications in various fields:
-
Finance: Representing debts, losses, or deficits in accounts.
-
Temperature: Measuring temperatures below zero degrees Celsius or Fahrenheit.
-
Elevation: Representing altitudes below sea level.
-
Physics: Describing forces, velocities, and other quantities with negative values.
Understanding negative number arithmetic is essential for interpreting and working with data in these and many other contexts.
Frequently Asked Questions (FAQ)
-
Q: Why does -(-4) become +4? A: This is a fundamental rule of mathematics. Two consecutive negative signs cancel each other out, resulting in a positive sign. Think of it as two operations: first, you are negating -4, then you are negating the result of that negation, returning to the original positive value.
-
Q: Can I add the numbers before considering the signs? A: No. You must always address the signs first. Failure to do so will lead to incorrect answers. Following the order of operations is crucial.
-
Q: What if the problem was (-4) + (-4)? A: In that case, you are adding two negative numbers. The result would be -8. This is a different operation from subtraction.
-
Q: Are there other methods to solve this problem? A: While the method outlined above is the most straightforward, you could use alternative methods involving absolute values, but the underlying principle of additive inverse remains crucial.
Conclusion: Mastering Negative Number Subtraction
The solution to -4 - (-4) is 0. This seemingly simple problem highlights the importance of understanding the rules of negative numbers, particularly the concept of the double negative and the additive inverse. By systematically applying these principles, you can confidently solve similar problems and navigate the world of negative number arithmetic. This understanding extends beyond simple equations, forming a solid foundation for more complex mathematical operations and problem-solving across various disciplines. Practice makes perfect, so try more examples and don't hesitate to review the concepts explained above to ensure a thorough understanding. Remember, mastering negative numbers is a crucial step in your mathematical journey.
Latest Posts
Latest Posts
-
0 083 Repeating As A Fraction
Sep 13, 2025
-
Can Photosynthesis Occur Without Light
Sep 13, 2025
-
How To Multiply Rational Numbers
Sep 13, 2025
-
Sample Space Of Two Dice
Sep 13, 2025
-
How To Find Leading Coefficient
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Negative 4 Minus Negative 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.