Negative 4 Plus Negative 4
zacarellano
Sep 15, 2025 · 5 min read
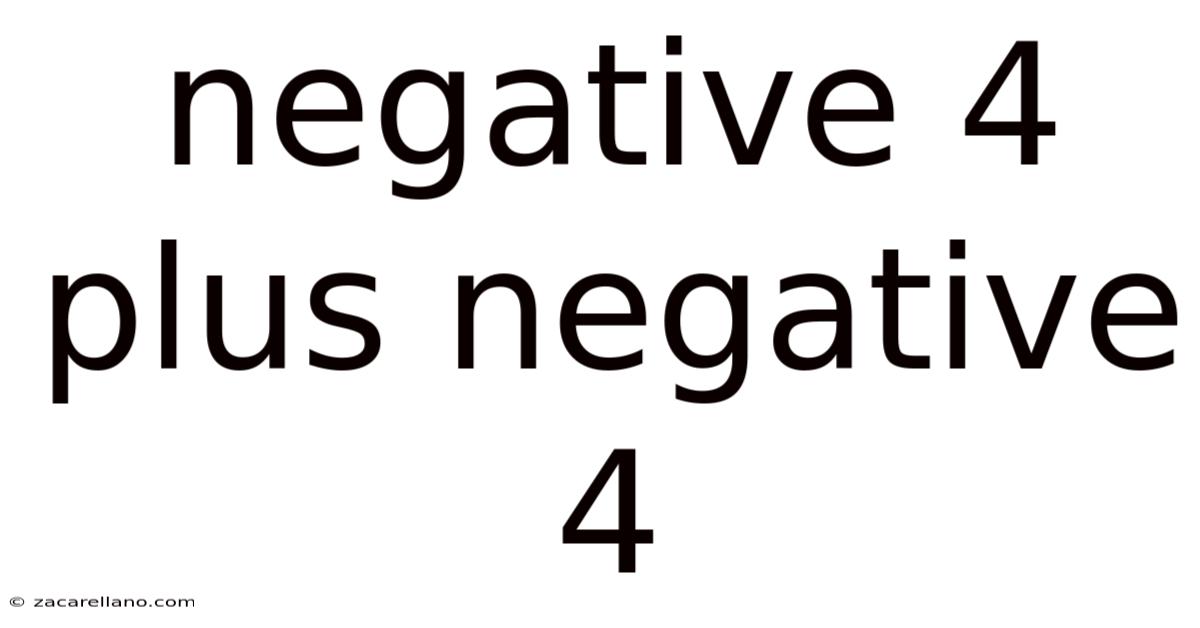
Table of Contents
Decoding the Mystery: Negative 4 Plus Negative 4 (-4 + -4)
Understanding basic arithmetic, especially involving negative numbers, is a fundamental building block for success in mathematics and beyond. This article will delve into the seemingly simple problem of -4 + -4, explaining not only the answer but also the underlying principles and broader applications. We will explore the concept of negative numbers, the rules of addition with negative numbers, and even touch upon real-world examples where understanding this concept is crucial. By the end, you'll not only know the answer to -4 + -4 but also possess a deeper understanding of integer addition.
Understanding Negative Numbers: A Conceptual Framework
Before jumping into the calculation, let's solidify our understanding of negative numbers. A negative number represents a value less than zero. Think of a number line: zero sits in the middle, with positive numbers stretching to the right and negative numbers extending to the left. Negative numbers are often used to represent things like debt, temperature below zero, or a decrease in quantity. They are essentially the opposites of positive numbers.
The Rules of Integer Addition: A Foundation for Understanding
The addition of integers (whole numbers, including negative numbers and zero) follows specific rules. These rules are crucial for accurately performing calculations involving negative numbers.
-
Adding two positive numbers: This is straightforward; you simply add the numbers together. For example, 2 + 3 = 5.
-
Adding a positive and a negative number: This involves finding the difference between the absolute values (ignoring the signs) of the numbers. The sign of the result is determined by the number with the larger absolute value. For example:
- 5 + (-2) = 3 (because 5 - 2 = 3, and the positive number has a larger absolute value).
- -5 + 2 = -3 (because 5 - 2 = 3, and the negative number has a larger absolute value).
-
Adding two negative numbers: This is where the concept of "adding debts" becomes helpful. When you add two negative numbers, you're essentially combining debts. The result is a larger negative number. You add the absolute values and keep the negative sign. For example, -2 + (-3) = -5.
Solving -4 + -4: A Step-by-Step Approach
Now, let's tackle our main problem: -4 + -4. Following the rules outlined above:
-
Identify the signs: Both numbers are negative.
-
Add the absolute values: The absolute value of -4 is 4. 4 + 4 = 8.
-
Assign the sign: Since both numbers were negative, the result retains the negative sign.
Therefore, -4 + -4 = -8.
Visualizing the Solution: The Number Line Approach
A number line can be a powerful tool for visualizing addition and subtraction with negative numbers. Start at -4 on the number line. Adding -4 means moving four units further to the left (in the negative direction). This brings you to -8.
Real-World Applications: Where Negative Numbers Matter
Understanding the addition of negative numbers isn't just an academic exercise; it has practical applications in various aspects of life:
-
Finance: Imagine you have a debt of $4 and you incur another debt of $4. Your total debt would be -$8. This scenario perfectly illustrates the principle of adding two negative numbers.
-
Temperature: If the temperature is -4°C and it drops by another 4°C, the new temperature would be -8°C. This real-world example shows the practical application of negative number addition.
-
Altitude: If a submarine is 4 meters below sea level (-4m) and descends another 4 meters, its new depth would be -8m.
-
Accounting: In accounting, negative numbers represent losses or expenses. Adding negative numbers helps in calculating the total losses or expenses.
-
Game Scores: In some games, negative scores can be awarded for penalties. Adding negative scores helps to determine the overall game score.
Expanding the Concept: Addition with More Than Two Negative Numbers
The principles we've discussed extend to situations involving more than two negative numbers. To add multiple negative numbers:
-
Add the absolute values of all the negative numbers.
-
Keep the negative sign in the final answer.
For example, -2 + (-3) + (-5) = -10
Beyond Addition: Subtraction with Negative Numbers
Subtracting a negative number is equivalent to adding its positive counterpart. This is a crucial concept to grasp. For example:
-
5 - (-2) = 5 + 2 = 7
-
-4 - (-3) = -4 + 3 = -1
This concept is based on the idea that subtracting a negative is the same as removing a debt, which effectively increases your positive value or reduces your negative value.
Addressing Common Misconceptions
A common mistake is to treat adding negative numbers as subtraction. While there's a relationship, it's essential to understand the distinction. Adding two negative numbers always results in a more negative number, not a positive one.
Frequently Asked Questions (FAQ)
Q: Why do we add the absolute values when adding two negative numbers?
A: Adding absolute values is a procedural step that simplifies the calculation. It focuses on the magnitude of the numbers, making it easier to determine the overall magnitude of the resulting negative number.
Q: Can we add a negative number and a positive number to get a zero?
A: Yes, absolutely! This happens when the absolute values of the positive and negative numbers are equal. For example, 5 + (-5) = 0. This is often referred to as the additive inverse.
Q: What if I have a series of positive and negative numbers to add?
A: You can group the positive numbers and add them separately, then group the negative numbers and add them separately. Finally, add the results (treating the sum of the negative numbers as a single negative number).
Conclusion: Mastering Negative Number Addition
Understanding the addition of negative numbers, such as solving -4 + -4, is essential for building a solid foundation in mathematics. By grasping the underlying principles and practicing regularly, you can confidently tackle more complex arithmetic problems involving integers. Remember that visualizing the problem using a number line, understanding the rules of integer addition, and recognizing real-world applications can significantly aid your understanding and boost your confidence in mathematical computations. The seemingly simple problem of -4 + -4 opens a door to a deeper understanding of the broader world of numbers and their applications. Keep practicing, keep exploring, and keep expanding your mathematical horizons!
Latest Posts
Latest Posts
-
Amino Terminal And Carboxy Terminal
Sep 15, 2025
-
Standard Deviation From Linear Regression
Sep 15, 2025
-
Math Worksheet For 1st Grade
Sep 15, 2025
-
How To Add Rational Functions
Sep 15, 2025
-
Art In The Victorian Era
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Negative 4 Plus Negative 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.