Negative 5 Minus Negative 7
zacarellano
Sep 19, 2025 · 5 min read
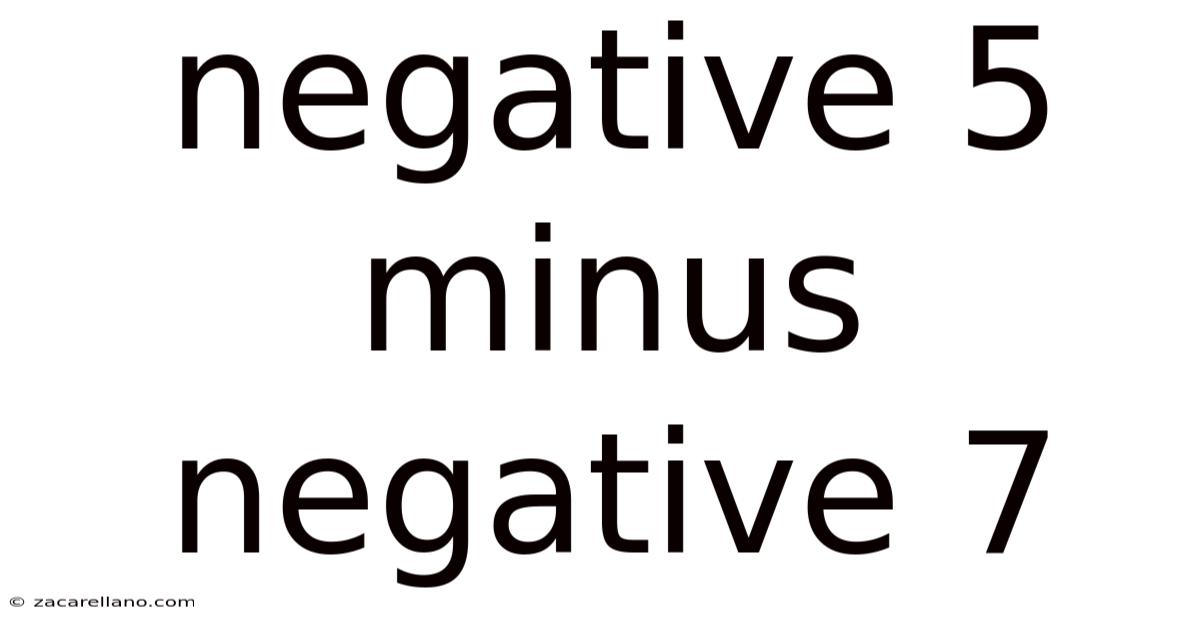
Table of Contents
Decoding the Mystery: Negative 5 Minus Negative 7
Understanding negative numbers can be tricky, but it's a fundamental concept in mathematics. This article will delve into the seemingly simple problem of negative 5 minus negative 7, explaining not just the answer but the underlying principles, providing a solid foundation for anyone struggling with integer arithmetic. We'll explore various methods to solve this problem, ensuring a comprehensive understanding of the concept. By the end, you'll be confident in tackling similar problems involving negative numbers.
Introduction: A World Beyond Zero
Before we jump into the specific calculation, let's establish a solid understanding of negative numbers. They represent values less than zero, extending the number line beyond the familiar positive integers. Think of a thermometer: temperatures below zero are represented by negative numbers. Similarly, in finance, a negative balance represents a debt. Mastering negative numbers is crucial for various mathematical applications, including algebra, calculus, and even programming.
Visualizing the Problem: The Number Line
A great way to visualize this problem – -5 - (-7) – is using the number line. Imagine a line stretching infinitely in both positive and negative directions. Zero is the central point. Negative numbers are to the left of zero, and positive numbers are to the right.
To solve -5 - (-7), we begin at -5 on the number line. Subtracting a negative number is equivalent to adding its positive counterpart. Think of it like this: removing a debt is the same as receiving money. Therefore, subtracting -7 is the same as adding +7.
So, starting at -5, we move 7 units to the right (positive direction). This leads us to the number 2. Therefore, -5 - (-7) = 2.
Step-by-Step Solution: Algebraic Approach
Let's break down the problem algebraically, focusing on the rules of operations with negative numbers:
-
Rewrite the expression: The expression -5 - (-7) can be rewritten as -5 + 7. Remember, subtracting a negative is the same as adding a positive. This is a key rule in mathematics involving integers.
-
Combine the numbers: Now, we simply add -5 and 7. Think of it as having a debt of 5 units and then receiving 7 units. After paying off the debt, you'll have 2 units left. Therefore, -5 + 7 = 2.
This algebraic approach reinforces the visual representation on the number line, providing a clear and concise method for solving the problem.
The Concept of Additive Inverses
The solution relies heavily on the concept of additive inverses. An additive inverse of a number is the number that, when added to the original number, results in zero. For example, the additive inverse of 5 is -5, because 5 + (-5) = 0. Similarly, the additive inverse of -7 is 7.
Understanding additive inverses is crucial because subtracting a number is equivalent to adding its additive inverse. This is why -5 - (-7) becomes -5 + 7.
Exploring Different Scenarios with Negative Numbers
To solidify our understanding, let's explore a few more examples involving negative numbers and subtraction:
-
-10 - (-3): Rewrite as -10 + 3 = -7. Starting at -10 on the number line and moving 3 units to the right brings us to -7.
-
-2 - (-8): Rewrite as -2 + 8 = 6. Starting at -2 and moving 8 units to the right leads to 6.
-
0 - (-4): Rewrite as 0 + 4 = 4. This illustrates that subtracting a negative from zero results in a positive number.
These examples highlight the consistent application of the rule: subtracting a negative number is the same as adding its positive counterpart.
The Importance of Parentheses
The parentheses in the original problem, -5 - (-7), are crucial. They dictate the order of operations. Without parentheses, the expression -5 - -7 might be misinterpreted. The parentheses clearly indicate that we are subtracting a negative number, not subtracting and then negating.
Real-World Applications: Beyond the Classroom
The concept of subtracting negative numbers is not limited to theoretical mathematics. It has many practical applications in various real-world scenarios:
-
Finance: Consider a bank account with a negative balance (debt). If you receive a payment (a reduction in debt), this is represented as subtracting a negative number.
-
Temperature: If the temperature is -5 degrees Celsius and it increases by 7 degrees, the new temperature is calculated by subtracting -7 from -5, resulting in 2 degrees Celsius.
-
Altitude: In aviation or mountaineering, negative altitudes represent depths below sea level. Calculating changes in altitude involves operations with negative numbers.
-
Programming: In computer programming, particularly in game development or simulations, handling negative numbers is essential for accurate calculations involving positions, speeds, or other variables.
Frequently Asked Questions (FAQ)
Q: Why is subtracting a negative number the same as adding a positive number?
A: Subtraction is the inverse operation of addition. When you subtract a negative number, you're essentially undoing the effect of adding that negative number. This "undoing" is equivalent to adding the positive counterpart.
Q: Can I solve this problem without using the number line or algebraic manipulation?
A: While less intuitive, you could consider the absolute values. The difference between -5 and -7 is 2. Since -7 is "greater" (less negative) than -5, the result is positive 2. This method works but relies on a good grasp of the number line implicitly.
Q: What if the problem was -7 - (-5)?
A: Following the same principle, -7 - (-5) becomes -7 + 5 = -2.
Q: Are there other methods to solve problems involving negative numbers?
A: Yes, there are. Methods like using number chips (visual aids representing positive and negative units) or employing different algebraic techniques can be used depending on the complexity of the problem and the level of mathematical understanding.
Conclusion: Mastering Negative Numbers
Understanding how to subtract negative numbers is a fundamental skill in mathematics. By mastering this concept, you'll build a stronger foundation for more advanced mathematical concepts. Remember the key rule: subtracting a negative number is the same as adding its positive counterpart. Use the number line, algebraic manipulation, or whichever method works best for you, to confidently tackle problems involving negative numbers, transforming them from daunting challenges into solvable equations. With consistent practice, you'll find yourself effortlessly navigating the world of integers and their operations. The initial difficulty in working with negative numbers will soon fade as you gain proficiency and confidence. Keep practicing, and you will be a master of negative number operations in no time!
Latest Posts
Latest Posts
-
Multiplication Of Rational Expressions Examples
Sep 19, 2025
-
Bohr Rutherford Diagram Of Helium
Sep 19, 2025
-
How To Write An Dbq
Sep 19, 2025
-
How To Solve Recursive Equations
Sep 19, 2025
-
X Equals Negative B Song
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Negative 5 Minus Negative 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.