Negative 5 Times Negative 5
zacarellano
Sep 14, 2025 · 6 min read
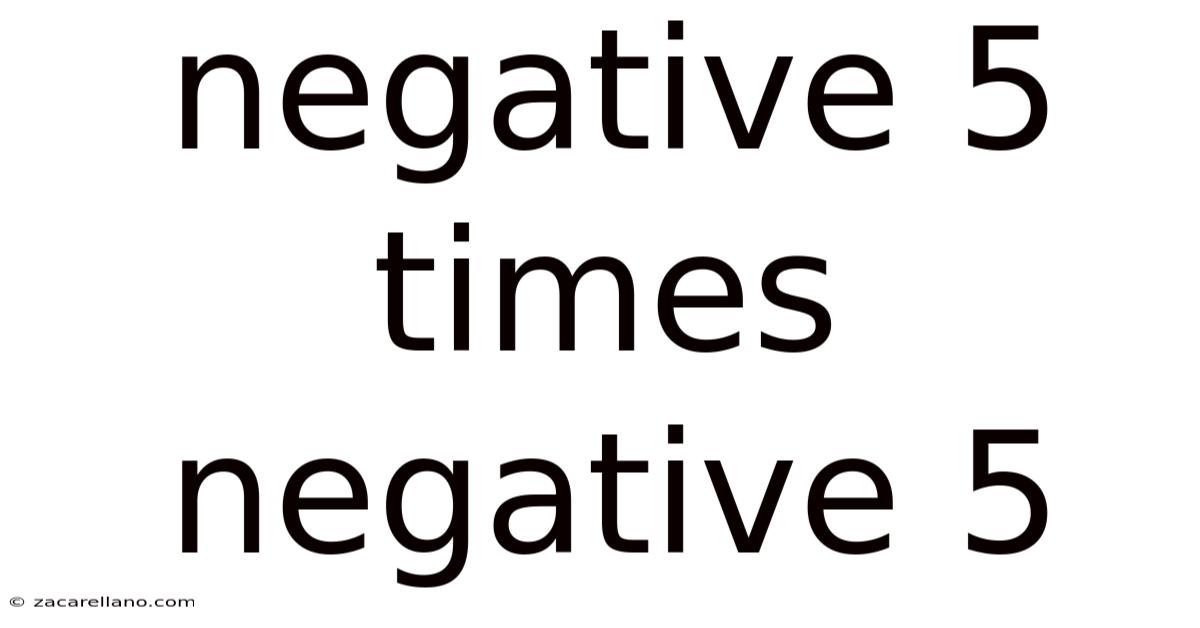
Table of Contents
Decoding the Mystery: Why Negative 5 Times Negative 5 Equals Positive 25
Understanding why a negative number multiplied by another negative number results in a positive number is a common stumbling block in mathematics. Many students memorize the rule – "negative times negative equals positive" – without truly grasping the underlying logic. This article will delve deep into the concept of multiplying negative numbers, specifically focusing on -5 x -5 = 25, using various approaches to illuminate this fundamental mathematical principle. We will explore the concept using number lines, patterns, and the distributive property, ultimately providing a comprehensive understanding that goes beyond simple rote memorization.
Introduction: Navigating the World of Negative Numbers
Negative numbers represent values less than zero. They extend the number line to the left of zero, creating a system that allows us to represent quantities like debt, temperature below freezing, or a decrease in value. While positive numbers are often intuitively grasped, negative numbers require a slightly different perspective. This article aims to bridge that understanding gap, particularly concerning multiplication involving negative numbers. The specific example of -5 x -5 = 25 will serve as our central focus, demonstrating the consistent application of the rules governing negative number multiplication.
Understanding Multiplication: A Foundational Perspective
Before diving into negative numbers, let's review the basic concept of multiplication. Multiplication is essentially repeated addition. For example, 5 x 3 means adding 5 three times: 5 + 5 + 5 = 15. This simple understanding forms the basis for extending the concept to negative numbers.
Exploring Patterns with Multiplication: A Visual Approach
Let's observe a pattern using multiplication with progressively decreasing numbers:
- 5 x 5 = 25
- 5 x 4 = 20
- 5 x 3 = 15
- 5 x 2 = 10
- 5 x 1 = 5
- 5 x 0 = 0
Notice that as the second number decreases by one, the product decreases by five. Let's continue the pattern, extending it into negative numbers:
- 5 x -1 = -5 (This is equivalent to adding -5 five times: -5 + -5 + -5 + -5 + -5)
- 5 x -2 = -10
- 5 x -3 = -15
- 5 x -4 = -20
- 5 x -5 = -25 (Wrong!)
Wait a minute, something doesn't seem right. We were expecting a consistent pattern. Why did the result not follow the established trend? Let’s try another approach.
The Number Line: A Visual Representation
Imagine a number line. Multiplication can be visualized on the number line as a series of jumps. For example, 5 x 3 means three jumps of 5 units to the right (positive direction). Now, consider 5 x -3. This means three jumps of 5 units to the left (negative direction), landing us at -15.
Now, let's explore -5 x 3. This can be interpreted as three jumps of negative 5 units, meaning three jumps of 5 units to the left, again resulting in -15.
Finally, consider -5 x -3. This represents three jumps of negative 5 units in the negative direction. Imagine starting at zero. If you were jumping negative units in the negative direction, each jump would actually move you to the right, towards the positive numbers! Three such jumps of 5 units each would land you at +15. This visual representation helps demonstrate the intuitive logic behind the positive outcome.
The Distributive Property: A Formal Mathematical Explanation
The distributive property states that a(b + c) = ab + ac. Let’s use this property to explain -5 x -5:
Consider the expression: -5 * (0) = 0. We know this is true because anything multiplied by zero equals zero.
Now let's rewrite 0 as (5 - 5):
-5 * (5 - 5) = 0
Applying the distributive property:
(-5 * 5) + (-5 * -5) = 0
We know that -5 * 5 = -25. Substituting this into the equation:
-25 + (-5 * -5) = 0
To solve for (-5 * -5), we add 25 to both sides of the equation:
-25 + 25 + (-5 * -5) = 0 + 25
This simplifies to:
(-5 * -5) = 25
The Concept of Inverse Operations: Adding another layer of Understanding
Multiplication and division are inverse operations. Similarly, addition and subtraction are inverse operations. Consider the following:
- 5 ÷ 5 = 1
- -5 ÷ 5 = -1
- -5 ÷ -5 = 1
Notice the pattern? When dividing two numbers with opposite signs (one positive and one negative), the result is negative. When dividing two numbers with the same sign (both positive or both negative), the result is positive.
This mirrors the rule for multiplication: Same signs result in a positive product; opposite signs result in a negative product.
Practical Applications: Where it Matters
Understanding the multiplication of negative numbers isn't just an abstract mathematical exercise; it has real-world applications:
- Finance: Calculating losses and debts. A loss of $5 per day for 5 days is a total loss of $25 (-5 x 5 = -25). A decrease in debt of $5 per day for 5 days represents an increase in net worth of $25 (-5 x -5 = 25).
- Physics: Calculating displacement and velocity. A change in speed and direction. A negative velocity could be a speed in the opposite direction. Multiplying these negative values provides useful information.
- Computer Programming: Many programming languages rely on the rules of arithmetic, including the multiplication of negative numbers, to perform calculations.
Frequently Asked Questions (FAQ)
Q: Why is it so important to understand negative number multiplication?
A: Mastering negative number multiplication is crucial for building a solid foundation in algebra, calculus, and other advanced mathematical concepts. It’s a fundamental skill that is applied extensively across various scientific and technical fields.
Q: Are there other ways to prove -5 x -5 = 25?
A: Yes, several other mathematical proofs can demonstrate this. The methods outlined above represent a selection of intuitive and easily understandable approaches.
Q: What if I still find this concept confusing?
A: Don't be discouraged! Mathematics can be challenging. Seek additional help from teachers, tutors, or online resources. Practice regularly with various examples to reinforce your understanding. Breaking down the problem into smaller steps and visualizing the process can greatly aid understanding.
Conclusion: A Comprehensive Understanding
The concept of negative number multiplication, exemplified by -5 x -5 = 25, might seem counterintuitive initially. However, by exploring patterns, using visual representations like the number line, applying the distributive property, and understanding the concept of inverse operations, we've established a comprehensive understanding of this fundamental mathematical principle. This isn't just about memorizing a rule; it's about grasping the underlying logic and its importance in various fields. With consistent practice and a deeper exploration of the concept, you'll build confidence and mastery in handling negative numbers and their operations. Remember, mastering this concept is a significant step towards unlocking more advanced mathematical concepts. Remember, mathematics is a journey of discovery, and persistent effort always pays off.
Latest Posts
Latest Posts
-
Fun 2nd Grade Math Worksheets
Sep 14, 2025
-
Volume Of The Great Pyramid
Sep 14, 2025
-
How To Calculate Oppurtunity Cost
Sep 14, 2025
-
Lewis Dot Structure Double Bond
Sep 14, 2025
-
Macro And Micro In Sociology
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Negative 5 Times Negative 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.