Negative 7 Minus Negative 2
zacarellano
Sep 16, 2025 · 5 min read
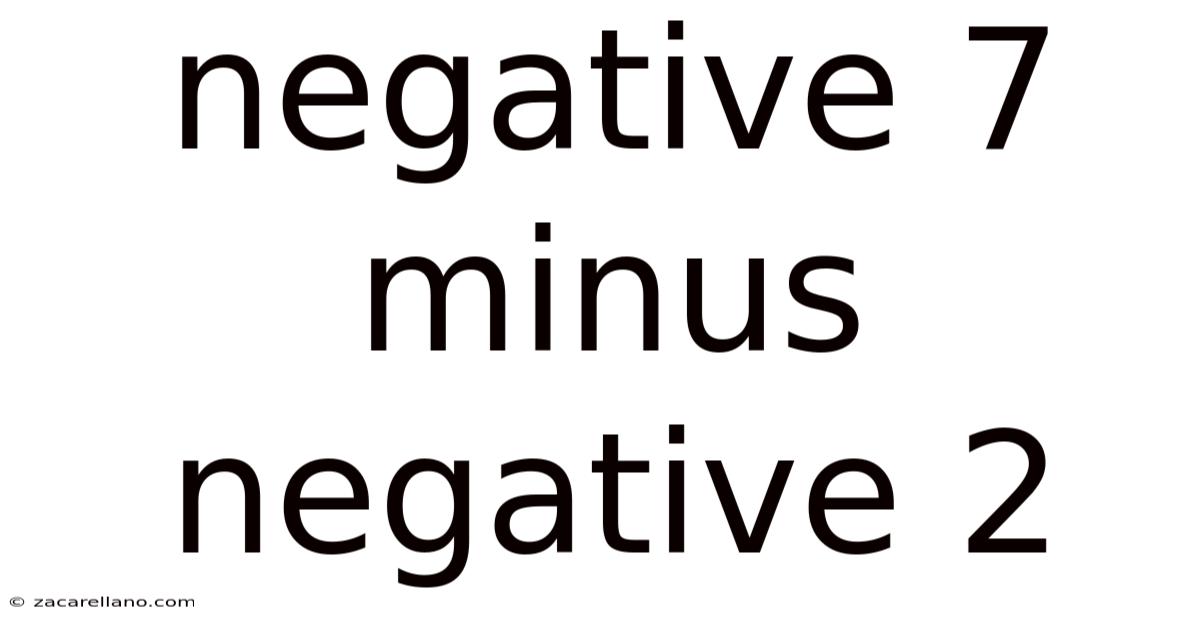
Table of Contents
Deconstructing -7 - (-2): A Deep Dive into Integer Subtraction
This article will explore the seemingly simple mathematical problem of -7 - (-2). While the answer might seem immediately obvious to some, a deeper understanding of integer subtraction, particularly involving negative numbers, reveals fundamental concepts crucial for mastering more complex mathematical operations. We'll break down the process step-by-step, delve into the underlying principles, and address common misconceptions, ensuring a comprehensive understanding for learners of all levels. This exploration will cover not just the solution but also the why behind the mechanics, making the concept truly stick.
Understanding Integer Subtraction
Before tackling -7 - (-2), let's establish a solid foundation in integer subtraction. Integers are whole numbers, including zero, and their negative counterparts (...-3, -2, -1, 0, 1, 2, 3...). Subtraction, at its core, represents the removal of a quantity from another. However, when dealing with negative integers, this concept requires careful consideration.
One helpful way to visualize subtraction is using a number line. Imagine -7 on a number line. Subtracting a positive number means moving to the left along the number line. Subtracting a negative number, however, is counterintuitive; it means moving to the right. This seemingly paradoxical behavior is at the heart of understanding integer subtraction.
The Additive Inverse: The Key to Understanding Negative Subtraction
The key to solving -7 - (-2) lies in the concept of the additive inverse. The additive inverse of a number is the number that, when added to the original number, results in zero. For example, the additive inverse of 5 is -5 (5 + (-5) = 0), and the additive inverse of -8 is 8 (-8 + 8 = 0).
Subtracting a number is equivalent to adding its additive inverse. This fundamental principle simplifies calculations involving negative numbers. Therefore, -7 - (-2) can be rewritten as -7 + (+2).
Step-by-Step Solution: -7 - (-2)
Now, let's solve the problem step-by-step:
-
Rewrite the expression: The initial problem, -7 - (-2), is rewritten using the additive inverse principle: -7 + (+2).
-
Simplify the signs: The expression becomes -7 + 2.
-
Perform the addition: We now have a simple addition problem involving integers with differing signs. Think of it as having a debt of 7 units and then receiving 2 units. The remaining debt is 5 units.
-
Final Answer: Therefore, -7 - (-2) = -5.
Visualizing the Solution on a Number Line
Let's visualize this on a number line:
- Start at -7.
- Subtracting -2 means moving two units to the right (because we're subtracting a negative).
- This lands us at -5.
Addressing Common Misconceptions
Many students struggle with subtracting negative numbers. Here are some common misconceptions and how to address them:
-
Confusing subtraction with negation: Subtraction and negation are distinct operations. Negation simply changes the sign of a number (e.g., the negation of 5 is -5). Subtraction involves finding the difference between two numbers.
-
Ignoring the double negative: Students sometimes forget that subtracting a negative number is equivalent to adding its positive counterpart. This often leads to incorrect answers. Emphasizing the additive inverse concept helps clarify this.
-
Incorrect application of order of operations: When dealing with more complex expressions, remembering the order of operations (PEMDAS/BODMAS) is crucial. Negative numbers should be handled correctly within the context of the order of operations.
Further Exploration: Expanding the Concept
The principles discussed above extend beyond simple two-number subtractions. Let's consider more complex examples:
-
-10 - (-5) - (-3): This can be rewritten as -10 + 5 + 3 = -2. Notice how each subtraction of a negative number turns into an addition.
-
-5 - (+3): This simplifies to -5 - 3 = -8. Subtracting a positive number moves you to the left on the number line.
Real-World Applications
Understanding integer subtraction is not just a theoretical exercise; it has practical applications in various fields:
-
Finance: Tracking profits and losses in accounting requires a strong understanding of negative numbers and their subtraction. A negative balance represents a debt.
-
Temperature: Calculating temperature differences often involves subtracting negative temperatures. For example, finding the difference between -10°C and -5°C.
-
Elevation: Mapping and surveying use negative numbers to represent elevations below sea level. Calculating differences in elevation frequently involves subtracting negative values.
-
Programming: Computer programming extensively uses integers and their operations, including subtraction, in various algorithms and data structures.
Frequently Asked Questions (FAQ)
Q1: Why does subtracting a negative number result in addition?
A1: Subtracting a number is the same as adding its additive inverse. The additive inverse of a negative number is its positive counterpart.
Q2: Can I use a calculator to solve these problems?
A2: Yes, calculators can handle integer subtraction, but understanding the underlying principles is essential for developing strong mathematical skills. Calculators should be used as tools to check your work, not to replace understanding.
Q3: What if I have a series of subtractions involving negative numbers?
A3: Rewrite each subtraction of a negative number as addition of the positive counterpart and then simplify the expression using the rules of addition.
Q4: How do I explain this to a younger student?
A4: Use real-world analogies like owing money (negative numbers) and receiving money (positive numbers). Subtracting a debt is the same as receiving money, thereby increasing your net worth. The number line visualization is also very helpful for younger learners.
Conclusion: Mastering Integer Subtraction
Mastering integer subtraction, particularly involving negative numbers, is a critical step in building a strong mathematical foundation. By understanding the concept of the additive inverse and visualizing the operations on a number line, the seemingly complex problem of -7 - (-2) becomes straightforward. The principles explored here extend to more complex calculations and have real-world applications in diverse fields. Remember to practice consistently and focus on grasping the underlying concepts rather than merely memorizing rules; this will enable you to solve a wide variety of mathematical problems confidently and accurately. Through consistent practice and a thorough understanding of the fundamentals, you'll not only confidently solve -7 - (-2) but also tackle any integer subtraction challenge with ease.
Latest Posts
Latest Posts
-
Ap Calc Ab Frq Answers
Sep 16, 2025
-
The Power Of Zero Summary
Sep 16, 2025
-
Heat Fusion Graph With Formula
Sep 16, 2025
-
Indian Ocean Trade Time Period
Sep 16, 2025
-
Word Problems For Adding Decimals
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Negative 7 Minus Negative 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.