Negative 7 Minus Negative 4
zacarellano
Sep 20, 2025 · 5 min read
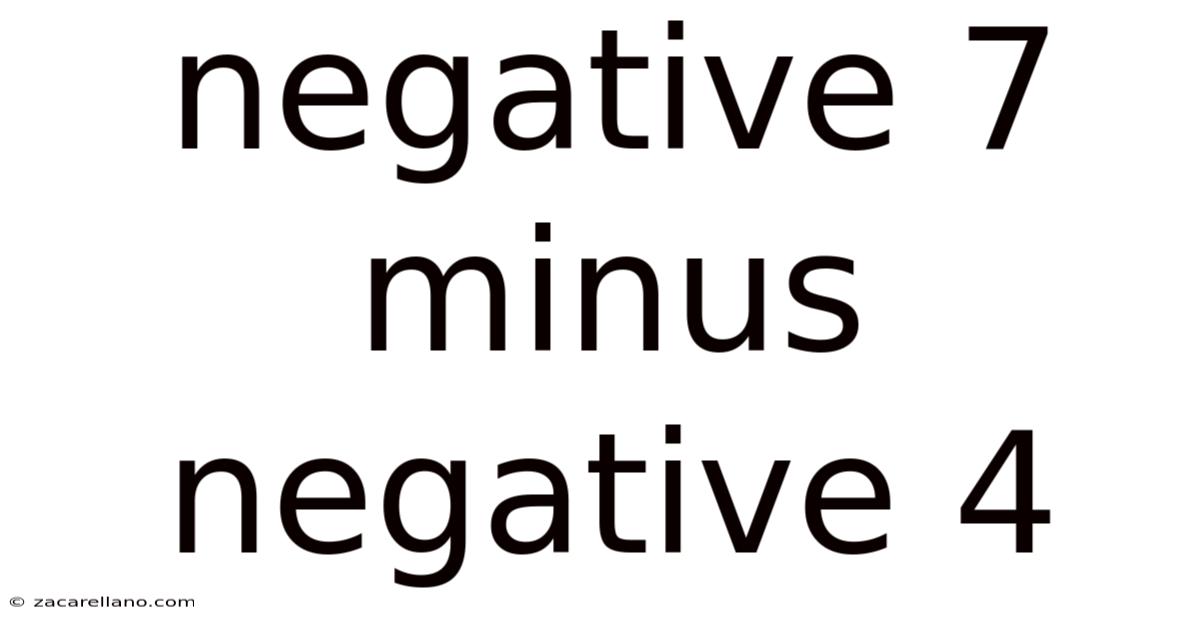
Table of Contents
Decoding the Mystery: Negative 7 Minus Negative 4
Understanding negative numbers can be tricky, but mastering them unlocks a world of mathematical possibilities. This article will delve into the seemingly complex problem of negative 7 minus negative 4, (-7 - (-4)), providing a step-by-step explanation, exploring the underlying mathematical principles, and addressing frequently asked questions. By the end, you’ll not only know the answer but also grasp the core concepts behind integer subtraction. This comprehensive guide will equip you with the tools to confidently tackle similar problems involving negative numbers.
Understanding Negative Numbers
Before we tackle the specific problem, let's build a solid foundation. Negative numbers represent values less than zero. They're often used to represent things like temperatures below freezing, debts, or positions below a reference point (like sea level). Visualizing them on a number line is extremely helpful. Imagine a number line stretching infinitely in both directions. Zero sits in the middle, positive numbers extend to the right, and negative numbers extend to the left.
The Concept of Subtraction
Subtraction, at its core, means taking away. If you have 5 apples and subtract 2, you're left with 3. However, when dealing with negative numbers, this concept needs a bit more nuance. Think of subtraction as finding the difference between two numbers. This difference represents the distance between the two numbers on the number line.
Breaking Down -7 - (-4)
Now let's tackle our problem: -7 - (-4). The key to solving this lies in understanding the concept of subtracting a negative number. Subtracting a negative number is the same as adding its positive counterpart. This is a crucial rule in mathematics.
Why does this work? Consider the number line. Subtracting a number moves you to the left. Subtracting a negative number means moving to the left of a negative number, which effectively moves you to the right, towards positive numbers – the same as adding a positive number.
Therefore, -7 - (-4) is equivalent to -7 + 4.
Step-by-Step Solution
-
Rewrite the expression: Transform the subtraction of a negative into the addition of a positive: -7 + 4.
-
Visualize on a Number Line: Start at -7 on the number line. Adding 4 means moving four units to the right.
-
Perform the Addition: Moving four units to the right from -7 brings us to -3.
-
The Solution: Therefore, -7 - (-4) = -3.
A Deeper Dive: The Mathematical Properties
The process we just followed relies on several key mathematical properties:
-
Additive Inverse: Every number has an additive inverse, which is the number that, when added to it, results in zero. The additive inverse of 4 is -4, and vice versa.
-
Associative Property of Addition: The grouping of numbers in an addition problem doesn't change the sum. For example, (a + b) + c = a + (b + c).
-
Commutative Property of Addition: The order of numbers in an addition problem doesn't change the sum. For example, a + b = b + a.
These properties underpin the manipulation of the equation and allow us to simplify the expression from -7 - (-4) to -7 + 4.
Real-World Applications
Understanding negative number subtraction isn't just an academic exercise; it has practical applications in various fields:
-
Finance: Calculating profits and losses, managing debts, and understanding bank balances often involve negative numbers.
-
Temperature: Meteorology relies on negative numbers to represent temperatures below zero. Calculating temperature differences requires understanding subtraction with negative numbers.
-
Altitude: Determining changes in elevation, especially in aviation or mountaineering, requires calculations involving negative numbers (representing depths below sea level).
-
Physics: In physics, negative numbers represent directions or quantities in the opposite direction to a reference point.
Expanding on the Concept: More Complex Problems
The principles explained here can be applied to more complex problems involving multiple negative numbers. For example:
-
-10 - (-5) - (-2): This can be rewritten as -10 + 5 + 2. Following the order of operations (from left to right), we get -5 + 2 = -3.
-
-3 - 7 - (-12): This becomes -3 - 7 + 12. Again, solving from left to right gives -10 + 12 = 2.
The key is always to remember that subtracting a negative is the same as adding a positive.
Frequently Asked Questions (FAQ)
Q: Why is subtracting a negative number the same as adding a positive number?
A: This stems from the concept of additive inverses and the properties of real numbers. Subtracting a number is equivalent to adding its additive inverse. Since the additive inverse of a negative number is its positive counterpart, subtracting a negative is the same as adding a positive.
Q: Can I use a calculator to solve problems involving negative numbers?
A: Absolutely! Most calculators will correctly handle negative numbers. Ensure you use the appropriate negative sign (usually a "-" button) and pay attention to the order of operations.
Q: What if I encounter a problem like -7 + (-4)?
A: Adding a negative number is the same as subtracting a positive number. So, -7 + (-4) is equivalent to -7 - 4, which equals -11.
Q: Is there a different way to visualize this besides the number line?
A: You could use colored chips to represent positive and negative numbers. Removing negative chips would be equivalent to adding positive chips.
Q: What happens if I subtract a larger negative number from a smaller negative number?
A: You'll end up with a negative result. For example, -2 - (-5) = -2 + 5 = 3 (a positive result because 5 is larger than 2). -5 - (-2) = -5 + 2 = -3 (a negative result).
Conclusion
Mastering negative number subtraction is a foundational step in developing strong mathematical skills. By understanding the underlying principles, you can confidently tackle even complex problems. Remember the key rule: subtracting a negative number is the same as adding its positive counterpart. This simple yet powerful concept opens the door to a deeper understanding of number systems and their applications in diverse fields. Practice regularly, and you'll soon find these calculations become second nature. The journey into the world of mathematics is rewarding, and understanding negative numbers is a vital step along the way.
Latest Posts
Latest Posts
-
Bronze Doors Of Bishop Bernward
Sep 20, 2025
-
Function Versus Not A Function
Sep 20, 2025
-
A 2 B 2 Factor
Sep 20, 2025
-
Lewis Dot Diagram Of Fluorine
Sep 20, 2025
-
Integration Of X 2 Ex
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Negative 7 Minus Negative 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.