Negative 7 Minus Negative 8
zacarellano
Sep 25, 2025 · 5 min read
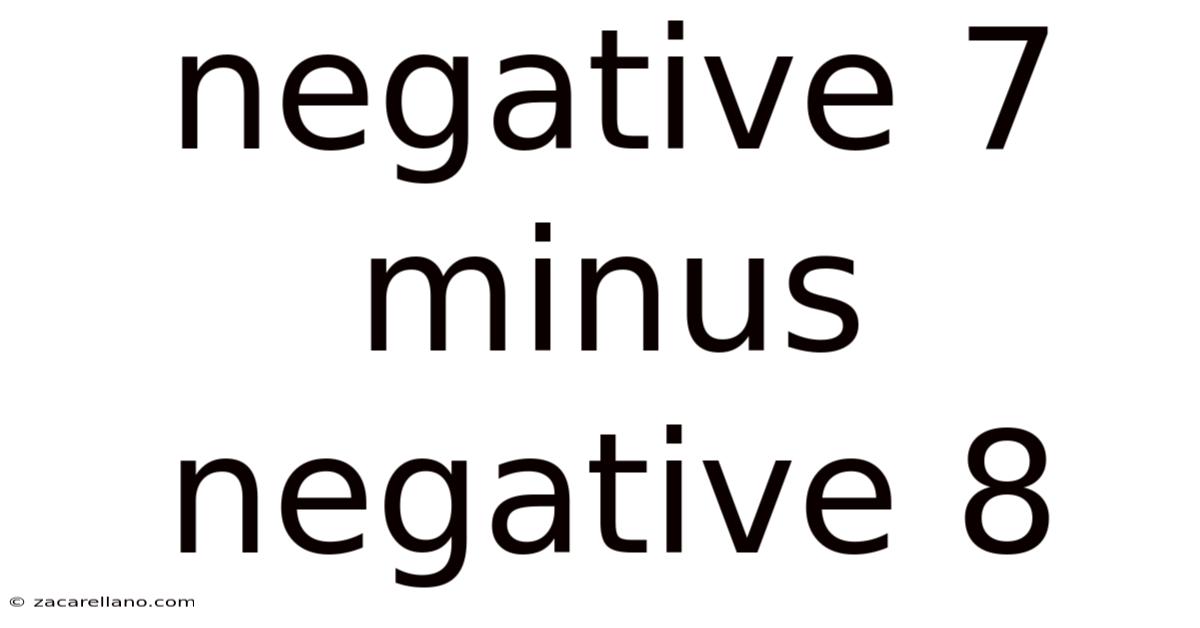
Table of Contents
Unraveling the Mystery: Negative 7 Minus Negative 8
Understanding negative numbers can be tricky, especially when subtraction is involved. This article will delve into the seemingly complex problem of "negative 7 minus negative 8," breaking down the concept step-by-step to provide a clear and comprehensive understanding. We'll explore the underlying mathematical principles, offer multiple approaches to solving the problem, and address frequently asked questions. By the end, you'll not only know the answer but also possess a solid foundation in working with negative numbers.
Introduction: Navigating the World of Negative Numbers
Negative numbers represent values less than zero. They extend the number line beyond zero to encompass quantities below it. While initially challenging, understanding negative numbers is crucial in various fields, from finance and accounting to physics and computer science. This article focuses on one specific operation involving negative numbers: subtraction. Specifically, we'll tackle the equation: -7 - (-8). This might appear confusing at first glance, but by breaking down the process, we can easily arrive at the correct answer and solidify our understanding of working with negative numbers.
Understanding Subtraction as Adding the Opposite
The key to solving problems involving subtracting negative numbers lies in understanding the concept of "adding the opposite." Subtraction can be redefined as the addition of the additive inverse (or opposite) of a number. The additive inverse of a number is simply the number with the opposite sign. For example:
- The additive inverse of 5 is -5.
- The additive inverse of -3 is 3.
Therefore, subtracting a negative number is equivalent to adding its positive counterpart. This is a fundamental concept that simplifies the process of solving equations involving negative numbers.
Step-by-Step Solution: -7 - (-8)
Let's apply this principle to our problem, -7 - (-8):
-
Identify the additive inverse: The additive inverse of -8 is +8.
-
Rewrite the equation: We can rewrite the original equation as -7 + (+8).
-
Perform the addition: Now, we have a simple addition problem: -7 + 8.
-
Find the difference: Since 8 is larger than 7, the result will be positive. The difference between 8 and 7 is 1.
-
Final Answer: Therefore, -7 - (-8) = 1.
Visualizing with a Number Line
A number line provides a visual representation that can aid in understanding the concept. Start at -7 on the number line. Subtracting -8 means moving to the right by 8 units (since we are adding the opposite). This brings us to the point representing +1.
Alternative Methods: Using Absolute Values
Another way to approach this problem is by using absolute values. The absolute value of a number is its distance from zero, always represented as a positive value. While this method might seem more complex for this specific problem, understanding it provides a broader foundation for more complicated scenarios.
-
Find the absolute values: | -7 | = 7 and | -8 | = 8.
-
Consider the signs: We have a negative number (-7) minus a negative number (-8). Since we're subtracting a smaller negative number from a larger negative number, the result will be positive.
-
Subtract the absolute values: 8 - 7 = 1.
-
Apply the sign: Since the result should be positive (as explained in step 2), the final answer is 1.
The Importance of Parentheses: Order of Operations
The parentheses in the original equation, -7 - (-8), are crucial. They indicate the order of operations. Without them, the expression would be interpreted differently, potentially leading to an incorrect answer. Parentheses ensure that we correctly apply the "adding the opposite" rule.
Extending the Concept: More Complex Examples
The principles discussed above extend to more complex problems involving multiple negative numbers and other mathematical operations. For instance, consider the problem: -5 - (-3) + (-2).
-
Rewrite as addition: -5 + 3 + (-2)
-
Combine the terms: -5 + 3 = -2. Then, -2 + (-2) = -4.
-
Final answer: Therefore, -5 - (-3) + (-2) = -4.
Understanding the process of adding the opposite remains fundamental even when dealing with multiple operations.
Real-World Applications: Where Negative Numbers Matter
Negative numbers are not just abstract mathematical concepts. They have practical applications in many real-world scenarios.
- Finance: Negative numbers represent debt or losses. Understanding subtraction with negative numbers is vital for balancing accounts and tracking financial transactions.
- Temperature: Negative numbers represent temperatures below zero. Calculating temperature differences often involves subtracting negative numbers.
- Elevation: Negative numbers can indicate elevations below sea level. Determining the difference in elevation between two points might require subtraction of negative numbers.
- Computer Science: Negative numbers are essential in computer programming and data representation. Many algorithms rely on the ability to manipulate negative numbers.
Frequently Asked Questions (FAQ)
Q: Why does subtracting a negative number result in addition?
A: Subtracting a number is equivalent to adding its opposite. This is a fundamental principle of mathematics that simplifies calculations involving negative numbers.
Q: What if I forget the rule of adding the opposite?
A: While remembering the rule is helpful, you can always visualize the problem on a number line. Starting at the first number, move to the left for subtraction and to the right for addition.
Q: Are there other ways to solve problems involving negative numbers?
A: Yes, you can use different techniques like absolute values or visualizing the problem with a number line, as mentioned earlier.
Q: How can I practice solving problems involving negative numbers?
A: Practice is key! Work through various examples, starting with simple problems and gradually increasing the complexity. Online resources and textbooks offer plenty of practice problems.
Conclusion: Mastering Negative Numbers
Mastering operations involving negative numbers, particularly subtraction, is a crucial step in developing a strong mathematical foundation. By understanding the concept of "adding the opposite" and practicing consistently, you can confidently tackle even complex problems involving negative numbers. This article has provided a comprehensive guide, breaking down the process step-by-step and offering multiple approaches to ensure a thorough understanding. Remember, practice is key to mastering any mathematical concept, and negative numbers are no exception. Through consistent effort and application of the principles explained, you'll find that working with negative numbers becomes increasingly intuitive and straightforward. The initial hurdle of understanding these concepts will eventually lead to a more confident and comprehensive grasp of mathematics as a whole.
Latest Posts
Latest Posts
-
Circuit Symbol For A Transistor
Sep 25, 2025
-
Lcm For 16 And 20
Sep 25, 2025
-
Elastic Collision Is Momentum Conserved
Sep 25, 2025
-
Verifying Trig Identities Practice Problems
Sep 25, 2025
-
Maths For Class 2 Worksheets
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Negative 7 Minus Negative 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.