Negative 8 Minus Negative 8
zacarellano
Sep 17, 2025 · 6 min read
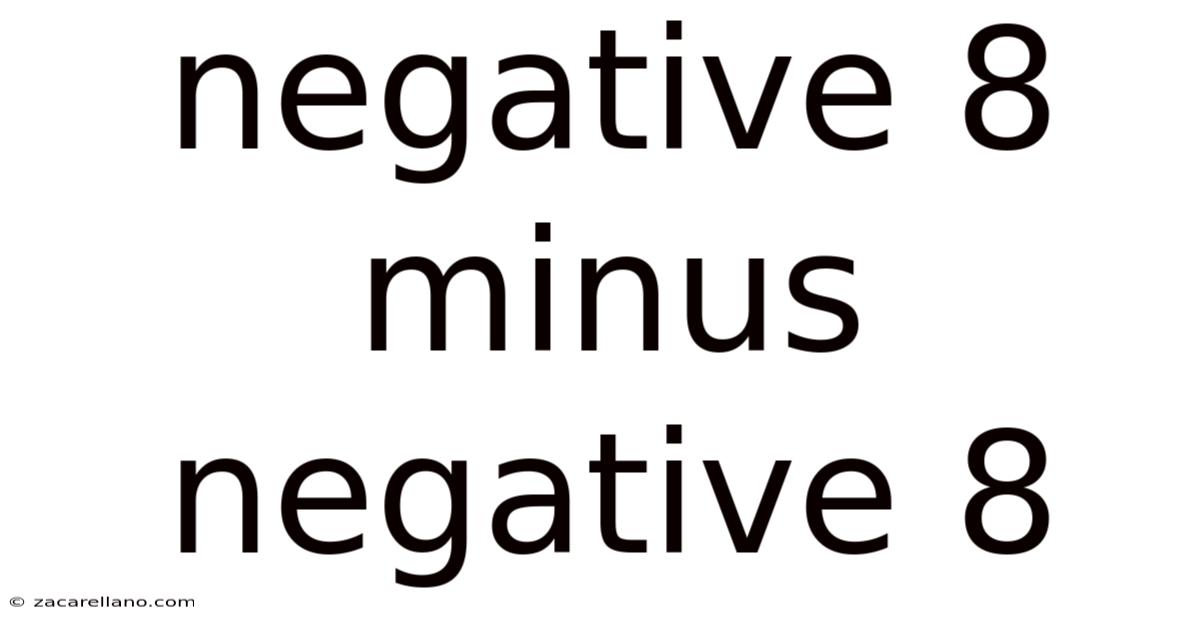
Table of Contents
Decoding the Mystery: Negative 8 Minus Negative 8
Understanding integers, particularly operations involving negative numbers, can sometimes feel like navigating a mathematical maze. This article will delve into the seemingly simple problem of negative 8 minus negative 8, exploring not just the solution but also the underlying principles of integer subtraction and its real-world applications. By the end, you'll not only know the answer but also possess a deeper understanding of how to tackle similar problems confidently. We'll explore the concept through various methods, clarifying any confusion and building a strong foundation in integer arithmetic.
Understanding Integers and the Number Line
Before tackling the problem, let's establish a firm understanding of integers. Integers are whole numbers, including zero, and their negative counterparts. They can be represented on a number line, with zero at the center, positive numbers extending to the right, and negative numbers extending to the left. This visual representation is crucial for understanding the concept of subtraction as a movement along the number line.
For instance, the number -8 is located eight units to the left of zero. Visualizing numbers on the number line helps to understand their relative positions and magnitudes. This will be particularly helpful when we explore subtraction.
Method 1: The Number Line Approach
The most intuitive way to approach "-8 - (-8)" is using the number line. Imagine yourself standing at -8 on the number line. Subtraction means moving to the left. However, we are subtracting a negative number (-8). Subtracting a negative is equivalent to adding a positive.
Think of it like this: You're already at -8. Subtracting a debt of 8 (represented as -8) means you are essentially gaining 8 units. Therefore, to solve -8 - (-8), we start at -8 and move 8 units to the right (because we're adding 8). This lands us precisely at 0.
Therefore, -8 - (-8) = 0
Method 2: The Additive Inverse
Another powerful concept to understand is the additive inverse. The additive inverse of a number is the number that, when added to the original number, results in zero. For any number 'a', its additive inverse is '-a'. For example, the additive inverse of 8 is -8, and the additive inverse of -8 is 8.
This understanding is key to solving our problem. The expression "-8 - (-8)" can be rewritten as "-8 + (+8)" using the concept of the additive inverse. Subtracting a negative is the same as adding its positive counterpart. This simplifies the equation considerably.
Now, we have -8 + 8. This is a simple addition problem, and the result is 0.
Therefore, -8 - (-8) = 0
Method 3: The Rules of Integer Subtraction
Let's formalize the rules of integer subtraction:
- Subtracting a positive number: Move to the left on the number line. For example, 5 - 3 = 2.
- Subtracting a negative number: Move to the right on the number line. This is equivalent to adding the positive version of that number. For example, 5 - (-3) = 5 + 3 = 8.
- Adding a positive number: Move to the right on the number line.
- Adding a negative number: Move to the left on the number line.
Applying these rules to our problem: -8 - (-8). Since we're subtracting a negative, we move to the right by 8 units from -8, which brings us to 0.
Therefore, -8 - (-8) = 0
Expanding the Understanding: Real-World Applications
While seemingly abstract, understanding integer operations has practical implications in various real-world scenarios:
- Finance: Think of negative numbers as debts or expenses. If you have a debt of $8 (-$8) and you pay off that debt (-(-$8)), your net balance becomes $0.
- Temperature: Imagine a temperature of -8°C. If the temperature increases by 8°C (-(-8°C)), the new temperature is 0°C.
- Elevation: If you are 8 meters below sea level (-8m) and you ascend 8 meters (-(-8m)), your new elevation is at sea level (0m).
- Accounting: In accounting, negative numbers represent losses or expenses. Subtracting a negative expense signifies a gain or reduction in expenses.
- Computer Programming: Integers are fundamental data types in programming, and understanding their operations is essential for writing algorithms and performing calculations.
These examples highlight how the seemingly simple problem of "-8 - (-8)" has practical relevance beyond the confines of a mathematics classroom.
Addressing Potential Confusion: Common Mistakes
While the solution is straightforward, some common misconceptions can arise:
- Ignoring the double negative: A frequent mistake is simply treating "-8 - (-8)" as "-8 - 8 = -16". This is incorrect. Remember, subtracting a negative is equivalent to adding a positive.
- Confusing subtraction with addition: Students may mistakenly add the numbers without considering the signs. -8 + (-8) is different from -8 - (-8).
- Lack of visualization: Without visualizing the operation on a number line or understanding the additive inverse, the solution might seem arbitrary.
To avoid these pitfalls, always remember the rules of integer operations and visualize the process using a number line.
Frequently Asked Questions (FAQ)
Q1: What is the difference between -8 - 8 and -8 - (-8)?
A1: -8 - 8 means you start at -8 on the number line and move 8 units to the left, resulting in -16. -8 - (-8) means you start at -8 and move 8 units to the right, resulting in 0. The key difference lies in the sign of the number being subtracted.
Q2: Can we solve this problem using different mathematical properties?
A2: Yes, we can use the associative property of addition to rearrange the terms. -8 - (-8) can be rewritten as -8 + 8, which then simplifies to 0.
Q3: Why is subtracting a negative the same as adding a positive?
A3: This stems from the definition of subtraction as adding the opposite. Subtracting a number is equivalent to adding its additive inverse. Since the additive inverse of a negative number is its positive counterpart, subtracting a negative number is essentially adding a positive number.
Q4: How can I practice more problems like this?
A4: Practice is key! Try solving similar problems with different integers, both positive and negative. Use the number line and the additive inverse concept to guide your calculations. You can also find many online resources and worksheets dedicated to integer arithmetic.
Conclusion
The seemingly simple problem of "-8 - (-8)" unveils the fundamental principles of integer subtraction and highlights the importance of understanding concepts like the additive inverse and the number line. By mastering these principles, you are not only equipped to solve this specific problem but also gain a robust foundation in integer arithmetic applicable to various mathematical and real-world situations. Remember to visualize, utilize the rules, and practice consistently to build your confidence and understanding. The solution, 0, is merely the tip of the iceberg in understanding the broader world of integer operations.
Latest Posts
Latest Posts
-
Unit 1 Algebra 1 Test
Sep 17, 2025
-
What Is Smaller Than Centimeters
Sep 17, 2025
-
Change In Quantity Demanded Definition
Sep 17, 2025
-
Distance From Acceleration And Time
Sep 17, 2025
-
Unit 7 Ap Bio Mcq
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Negative 8 Minus Negative 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.