Rules For Dividing Negative Numbers
zacarellano
Sep 21, 2025 · 6 min read
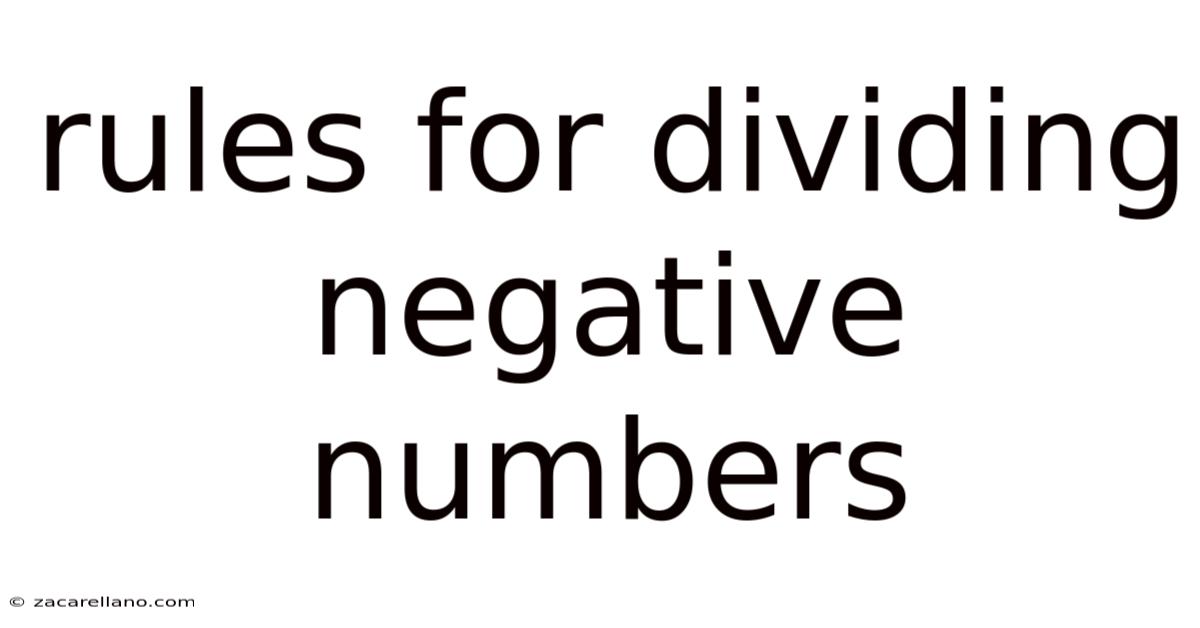
Table of Contents
Mastering the Art of Dividing Negative Numbers: A Comprehensive Guide
Dividing negative numbers can seem daunting at first, but with a clear understanding of the rules and underlying principles, it becomes straightforward. This comprehensive guide will walk you through the process, explaining not just the how but also the why, ensuring you develop a robust understanding of this fundamental mathematical operation. We'll explore different scenarios, address common misconceptions, and provide plenty of examples to solidify your learning. By the end, you'll be confident in dividing negative numbers and ready to tackle more complex mathematical problems.
Understanding the Fundamentals: Signs and Operations
Before diving into division specifically, let's refresh our understanding of positive and negative numbers and how they interact during arithmetic operations. The key concept lies in the sign of a number – positive (+) or negative (-). These signs indicate the number's position relative to zero on the number line.
-
Positive Numbers: These numbers are located to the right of zero on the number line and represent quantities greater than zero. They are usually written without a preceding plus sign (e.g., 5, 10, 100).
-
Negative Numbers: These numbers are located to the left of zero on the number line and represent quantities less than zero. They are always preceded by a minus sign (e.g., -5, -10, -100).
The rules for multiplying and dividing numbers with different signs are crucial:
-
Multiplying/Dividing Numbers with the Same Sign: If both numbers are positive or both are negative, the result is always positive.
- (+5) x (+2) = +10
- (-5) x (-2) = +10
- (+10) / (+2) = +5
- (-10) / (-2) = +5
-
Multiplying/Dividing Numbers with Different Signs: If one number is positive and the other is negative, the result is always negative.
- (+5) x (-2) = -10
- (-5) x (+2) = -10
- (+10) / (-2) = -5
- (-10) / (+2) = -5
These rules are fundamental and apply consistently across all mathematical operations involving negative numbers. Remember, the sign is an integral part of the number's value.
The Rules for Dividing Negative Numbers: A Step-by-Step Approach
Now, let's focus specifically on dividing negative numbers. The process is straightforward, and you can follow these simple steps:
-
Ignore the signs: Initially, ignore the negative signs and perform the division as you would with positive numbers. Focus solely on the magnitude (absolute value) of the numbers.
-
Determine the sign of the result: After completing the division of the magnitudes, determine the sign of the final answer based on the rules we discussed earlier. If the two numbers have the same sign (both positive or both negative), the result is positive. If they have different signs (one positive, one negative), the result is negative.
Let's illustrate with some examples:
Example 1: -12 ÷ -3
-
Ignore the signs: 12 ÷ 3 = 4
-
Determine the sign: Both numbers are negative, so the result is positive.
Therefore, -12 ÷ -3 = +4
Example 2: -15 ÷ 5
-
Ignore the signs: 15 ÷ 5 = 3
-
Determine the sign: One number is negative, and the other is positive, so the result is negative.
Therefore, -15 ÷ 5 = -3
Example 3: 20 ÷ -4
-
Ignore the signs: 20 ÷ 4 = 5
-
Determine the sign: One number is positive, and the other is negative, so the result is negative.
Therefore, 20 ÷ -4 = -5
Example 4: -25 ÷ -5
-
Ignore the signs: 25 ÷ 5 = 5
-
Determine the sign: Both numbers are negative, so the result is positive.
Therefore, -25 ÷ -5 = +5
These examples demonstrate the consistent application of the rules. By separating the magnitude and sign aspects of the division, you can systematically arrive at the correct answer.
Mathematical Justification: The Number Line and Inverse Operations
The rules for dividing negative numbers aren't arbitrary; they stem from the fundamental properties of numbers and operations. Let's explore this through the concept of inverse operations and the number line.
Division is the inverse operation of multiplication. This means that if a ÷ b = c, then c x b = a. Let's use this to illustrate why dividing two negative numbers results in a positive number.
Consider the equation -12 ÷ -3 = x. The inverse operation would be x x -3 = -12. What value of 'x' satisfies this equation? Only +4 does: (+4) x (-3) = -12. This demonstrates that the result of dividing two negative numbers must be positive to maintain consistency with the inverse operation.
Visualizing on the number line further clarifies this. Division can be seen as repeated subtraction. When dividing -12 by -3, you're asking, "How many times can I subtract -3 from -12 to reach 0?" Subtracting -3 is the same as adding +3. Therefore, you're essentially repeatedly adding +3 to -12: -12 + 3 + 3 + 3 + 3 = 0. You add +3 four times, confirming that -12 ÷ -3 = +4.
Dealing with Zero: Division by Zero and Other Special Cases
One crucial point to remember is that division by zero is undefined. This applies regardless of the sign of the numerator. You cannot divide any number by zero. It's an undefined operation in mathematics.
However, dividing zero by any non-zero number always results in zero: 0 ÷ (+5) = 0 and 0 ÷ (-5) = 0.
Common Mistakes to Avoid
While the rules for dividing negative numbers are straightforward, some common mistakes can arise:
-
Confusing the signs: The most common mistake is incorrectly determining the sign of the result. Carefully consider the signs of both numbers before determining whether the final answer should be positive or negative.
-
Forgetting the order of operations: If the expression involves multiple operations (addition, subtraction, multiplication, division), remember to follow the order of operations (PEMDAS/BODMAS).
-
Incorrectly applying the distributive property: Remember, the distributive property only applies to multiplication and division over addition and subtraction, not the other way around.
Frequently Asked Questions (FAQ)
Q1: Why does dividing two negative numbers result in a positive number?
A1: This is a consequence of the inverse relationship between multiplication and division. The rule ensures consistency across operations. Consider the inverse operation: if -12 ÷ -3 = 4, then 4 x -3 = -12, which is true.
Q2: Is there an easy way to remember the sign rules for division?
A2: Yes. Think of it as a simple pattern: Same signs (both positive or both negative) result in a positive answer. Different signs (one positive, one negative) result in a negative answer.
Q3: What happens if I divide a positive number by a negative number?
A3: The result will always be negative. Remember the rule: different signs yield a negative result.
Q4: Can I use a calculator to check my answers when dividing negative numbers?
A4: Yes, absolutely! Calculators are a valuable tool for checking your work and confirming your understanding of the rules.
Q5: Are there any real-world applications of dividing negative numbers?
A5: Yes, many! Negative numbers represent quantities like debt, temperature below zero, or loss in finance. Dividing negative numbers is crucial in various contexts, like calculating average losses or determining rates of decrease.
Conclusion: Mastering Negative Number Division
Dividing negative numbers may seem challenging initially, but by understanding the fundamental rules and their underlying principles, this operation becomes manageable and even intuitive. Remember to focus on the magnitude first, then apply the sign rules consistently. Practice is key to mastering this skill. With consistent effort and attention to detail, you'll develop confidence and proficiency in handling negative numbers in all mathematical contexts. This understanding forms a crucial foundation for more advanced mathematical concepts and problem-solving. Don't hesitate to review the steps and examples provided here, and soon you'll be dividing negative numbers with ease and accuracy!
Latest Posts
Latest Posts
-
Negative Feedback Vs Positive Feedback
Sep 21, 2025
-
Imagenes Del Ciclo Del Agua
Sep 21, 2025
-
Gcf Of 36 And 27
Sep 21, 2025
-
Does A Base Accept Protons
Sep 21, 2025
-
Solving Absolute Value Equations Worksheet
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Rules For Dividing Negative Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.