Simplify X 3 X 4
zacarellano
Sep 21, 2025 · 5 min read
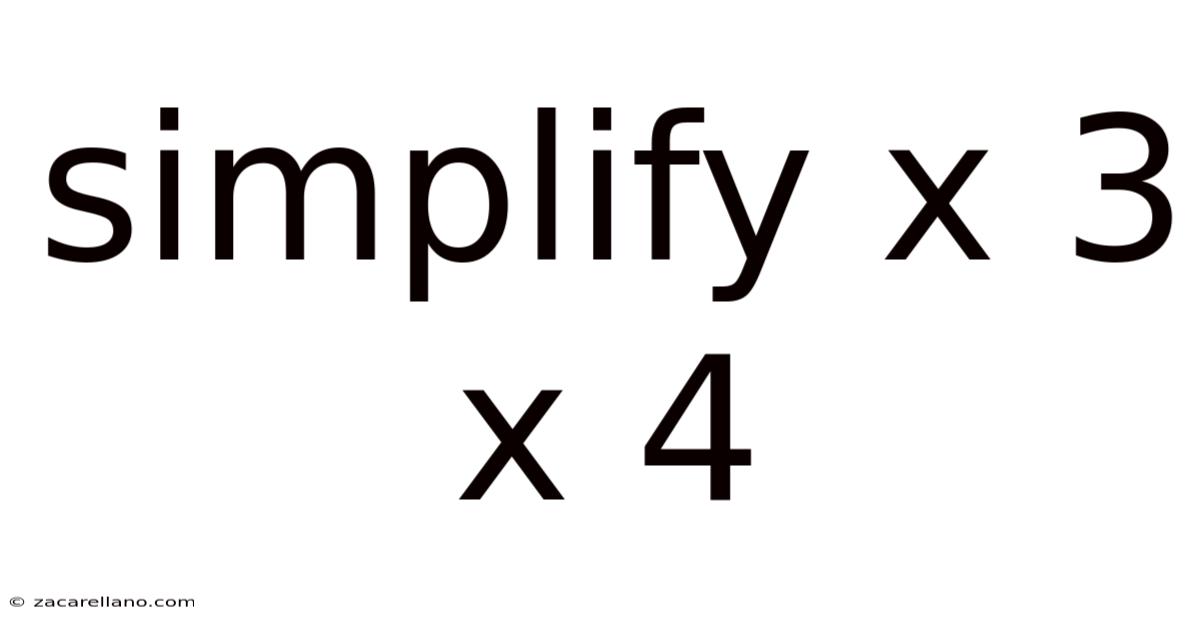
Table of Contents
Simplifying x × 3 × 4: A Deep Dive into Mathematical Simplification
This article explores the seemingly simple mathematical expression "x × 3 × 4," providing a comprehensive understanding of its simplification and broader implications within the field of algebra. We'll move beyond a simple answer and delve into the underlying principles, exploring different approaches and connecting this concept to more complex mathematical operations. This will be invaluable for students learning basic algebra and for anyone wishing to refresh their foundational mathematical skills.
Introduction: Understanding the Basics of Simplification
Simplification, in mathematics, is the process of reducing a mathematical expression to its simplest form. This often involves combining like terms, eliminating redundant operations, and presenting the expression in a more concise and manageable format. In the case of "x × 3 × 4," simplification aims to express the relationship between 'x' and the constants 3 and 4 in the most efficient way possible. This seemingly basic concept is fundamental to more advanced algebraic manipulations and problem-solving.
Step-by-Step Simplification of x × 3 × 4
The expression "x × 3 × 4" involves multiplication only. The commutative and associative properties of multiplication allow us to rearrange and group the terms in any order without changing the result.
-
Commutative Property: This property states that the order of multiplication doesn't affect the product. This means x × 3 × 4 is the same as 3 × x × 4, 4 × 3 × x, and so on.
-
Associative Property: This property allows us to group terms differently without changing the result. For instance, (x × 3) × 4 is the same as x × (3 × 4).
Using these properties, we can simplify the expression as follows:
x × 3 × 4 = x × (3 × 4) (Applying the associative property) = x × 12 (Performing the multiplication of the constants)
Therefore, the simplified form of x × 3 × 4 is 12x.
Beyond the Simple Answer: Exploring the Underlying Principles
While the simplification itself is straightforward, understanding the principles behind it is crucial for tackling more complex problems. Let's explore some of these principles in more detail:
-
Order of Operations (PEMDAS/BODMAS): While this expression only involves multiplication, understanding the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is essential for more complex expressions. This order ensures consistent results regardless of how the problem is approached.
-
The Distributive Property: Although not directly applied here, the distributive property (a × (b + c) = a × b + a × c) is a fundamental concept closely related to simplification. It allows us to expand and simplify expressions involving parentheses. Understanding this property is essential for tackling more complex algebraic equations.
-
Variables and Constants: The expression highlights the difference between variables (represented by 'x' which can take on various values) and constants (the numbers 3 and 4, which have fixed values). Simplification often involves manipulating variables and constants to express relationships in a clearer manner.
-
Coefficients: In the simplified expression 12x, '12' is the coefficient of 'x'. The coefficient represents the multiplicative factor of the variable. Understanding coefficients is important for solving equations and interpreting mathematical models.
Application in Real-World Scenarios
This seemingly simple simplification has numerous real-world applications. Consider these examples:
-
Calculating Costs: If 'x' represents the cost of a single item, and you buy 3 sets of 4 of these items, the total cost would be 12x.
-
Area Calculation: If 'x' represents the length of a rectangle, and the width is 3 units and the height is 4 units, the volume is 12x cubic units.
-
Geometry Problems: Many geometric problems involve multiplying lengths, widths, and heights to calculate area or volume. Simplification techniques are essential in solving such problems efficiently.
Expanding the Concept: More Complex Scenarios
Let's explore more complex scenarios to solidify our understanding of simplification:
Scenario 1: Incorporating Addition and Subtraction
Consider the expression: 2x + x × 3 × 4
-
Simplify the multiplication first: x × 3 × 4 = 12x
-
Combine like terms: 2x + 12x = 14x
Therefore, the simplified form is 14x.
Scenario 2: Including Parentheses
Consider the expression: 3(x × 2 × 4) + 5x
-
Simplify the expression inside the parentheses: x × 2 × 4 = 8x
-
Apply the distributive property: 3(8x) = 24x
-
Combine like terms: 24x + 5x = 29x
Therefore, the simplified form is 29x.
Scenario 3: Dealing with Exponents
Consider the expression: x² × 3 × 4
-
Simplify the constants: 3 × 4 = 12
-
The simplified form is 12x². Note that the exponent remains unchanged as it operates on 'x' only.
Frequently Asked Questions (FAQ)
-
Q: Can I simplify x × 3 × 4 in a different order?
A: Yes, due to the commutative and associative properties of multiplication, you can rearrange the terms in any order. The result will always be 12x.
-
Q: What if there were negative numbers involved?
A: The principles remain the same. Remember the rules for multiplying positive and negative numbers. For example, x × (-3) × 4 = -12x.
-
Q: Is there a limit to how complex an expression can get before needing simplification?
A: No. Simplification is always beneficial, especially as expressions become more complex. It improves readability, reduces the potential for errors, and makes solving equations easier.
-
Q: Why is simplification important?
A: Simplification is crucial for clarity, efficiency, and accuracy in mathematical problem-solving. It's a fundamental skill that underpins more advanced mathematical concepts.
Conclusion: Mastering Simplification for Future Success
Simplifying the expression x × 3 × 4, while seemingly trivial, offers a gateway to understanding fundamental algebraic principles. Mastering these principles, such as the commutative and associative properties, the distributive property, and the order of operations, builds a solid foundation for tackling more complex algebraic expressions and equations. The ability to simplify effectively is a critical skill that will continue to serve you well throughout your mathematical journey, from solving basic arithmetic problems to tackling advanced calculus. Remember the importance of understanding why a simplification works, not just how it works. This deeper understanding will unlock your potential to solve more complex mathematical challenges with confidence and accuracy.
Latest Posts
Latest Posts
-
How To Find Power Series
Sep 21, 2025
-
3 Digit Addition Word Problems
Sep 21, 2025
-
Single Replacement And Double Replacement
Sep 21, 2025
-
1 1 2 Yards To Inches
Sep 21, 2025
-
Photosynthesis Occurs In Which Organelle
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Simplify X 3 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.