Square Root Of 2 1
zacarellano
Sep 17, 2025 · 6 min read
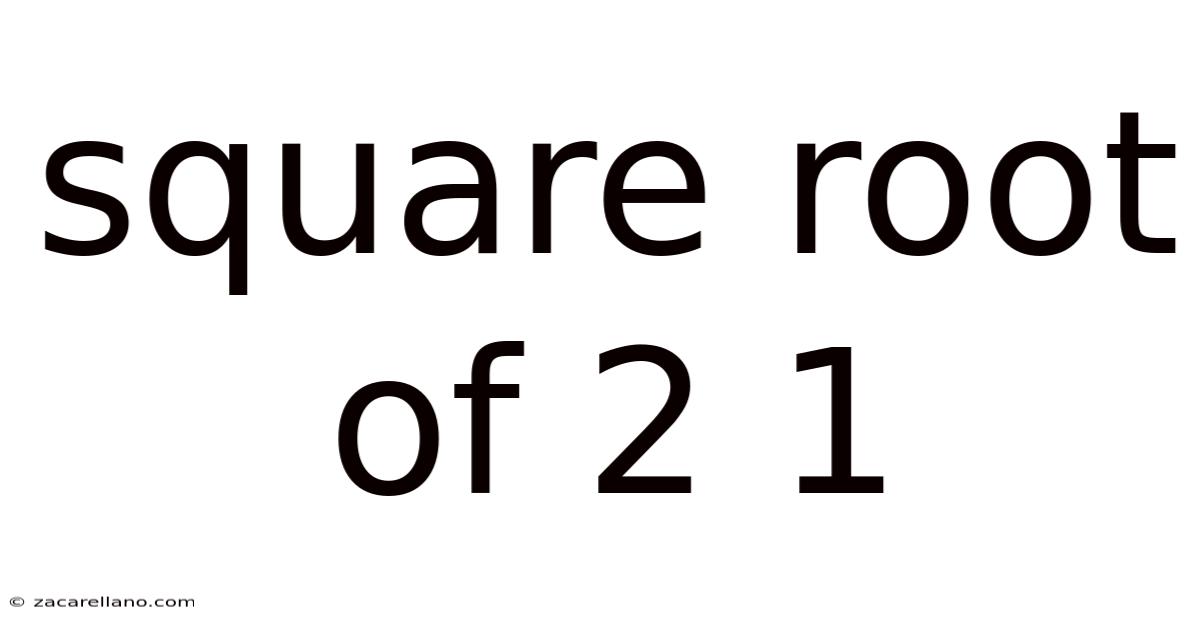
Table of Contents
Decoding the Enigma: A Deep Dive into the Square Root of 2
The square root of 2, denoted as √2 or 2<sup>1/2</sup>, is a seemingly simple mathematical concept, yet it holds a profound significance in the history of mathematics and continues to fascinate mathematicians and students alike. This seemingly innocuous number, approximately 1.414, represents the length of the diagonal of a unit square – a geometric truth that has implications far beyond its initial simplicity. This article will explore the square root of 2 from its historical context to its modern applications, delving into its irrationality, its geometric interpretations, and its enduring presence in various fields.
The Dawn of Irrationality: A Historical Perspective
The discovery of the square root of 2 is often credited to the Pythagorean school of ancient Greece, though the exact circumstances remain shrouded in mystery. The Pythagoreans, known for their reverence of whole numbers and their belief in the harmony of the cosmos, were deeply shaken by the realization that this seemingly simple number could not be expressed as a ratio of two whole numbers – a rational number. This discovery shattered their worldview and marked a pivotal moment in the development of mathematics. The proof of its irrationality, often attributed to the method of contradiction, represents a cornerstone of mathematical reasoning.
The legend surrounding the discovery often portrays a sense of secrecy and even suppression of this revolutionary finding. The notion that the seemingly perfect world of numbers contained an irrational element was deeply unsettling. The story emphasizes the significance of this discovery in expanding the understanding of numbers and pushing the boundaries of mathematical thought. This historical context adds a layer of intrigue to the seemingly simple concept of √2.
Proving the Irrationality of √2: A Classic Proof by Contradiction
The classic proof of the irrationality of √2 uses the elegant method of reductio ad absurdum, or proof by contradiction. Let's explore this fundamental proof:
-
Assumption: Assume, for the sake of contradiction, that √2 is a rational number. This means it can be expressed as a fraction a/b, where a and b are integers, b ≠ 0, and a and b are coprime (meaning they share no common factors other than 1).
-
Squaring Both Sides: Squaring both sides of the equation √2 = a/b gives us 2 = a²/b².
-
Rearranging the Equation: Rearranging the equation, we get 2b² = a². This equation implies that a² is an even number (since it's equal to 2 times another integer).
-
Deduction about 'a': If a² is even, then 'a' itself must also be even. This is because the square of an odd number is always odd. Therefore, we can express 'a' as 2k, where k is an integer.
-
Substituting and Simplifying: Substituting a = 2k into the equation 2b² = a², we get 2b² = (2k)² = 4k².
-
Solving for b²: Dividing both sides by 2, we obtain b² = 2k². This equation implies that b² is also an even number.
-
Deduction about 'b': Following the same logic as before, if b² is even, then 'b' must also be even.
-
The Contradiction: We've now shown that both 'a' and 'b' are even numbers. However, this contradicts our initial assumption that a and b are coprime (they share no common factors other than 1). Since both are even, they share a common factor of 2.
-
Conclusion: This contradiction proves that our initial assumption – that √2 is rational – must be false. Therefore, √2 is an irrational number.
This proof, simple yet elegant, demonstrates the power of mathematical reasoning and highlights the fundamental difference between rational and irrational numbers.
Geometric Interpretation: The Diagonal of a Unit Square
The square root of 2 has a beautiful geometric interpretation. Consider a square with sides of length 1 unit. According to the Pythagorean theorem, the length of the diagonal (d) of this square is given by:
d² = 1² + 1² = 2
Therefore, the length of the diagonal is √2. This simple geometric representation provides an intuitive understanding of the number's value and its connection to fundamental geometric principles. This connection underscores the intimate relationship between geometry and algebra.
√2 in the Real World: Applications Across Disciplines
While seemingly abstract, the square root of 2 finds applications in numerous real-world scenarios:
-
Construction and Engineering: The square root of 2 is crucial in various construction and engineering calculations. It's used in determining diagonal measurements, optimizing building layouts, and ensuring structural integrity. Consider the precise measurements required in creating perfectly square structures – understanding √2 is essential for accuracy.
-
Computer Graphics and Game Development: In computer graphics and game development, √2 plays a role in calculating distances and rotations in two-dimensional space. Understanding vector calculations and the use of the Pythagorean theorem, which inherently involves √2, is critical for creating realistic and functional virtual environments.
-
Physics and Engineering: It appears in various physics formulas, including calculations related to velocity, acceleration, and forces acting at angles. Applications range from simple projectile motion calculations to more complex problems in mechanics and electromagnetism.
-
Music Theory: Surprisingly, √2 finds its way into music theory. Certain musical intervals and ratios are based on this irrational number, leading to harmonious sounds and aesthetically pleasing musical compositions. The relationship between mathematical ratios and musical harmony has captivated mathematicians and musicians for centuries.
Beyond the Basics: Approximations and Continued Fractions
While √2 cannot be expressed as a simple fraction, it can be approximated using various methods:
-
Decimal Approximation: The decimal approximation of √2 is approximately 1.41421356... This is an unending, non-repeating decimal, further highlighting its irrationality.
-
Continued Fractions: √2 can also be represented as a continued fraction: 1 + 1/(2 + 1/(2 + 1/(2 + ...))). This representation offers a unique way to approximate the value of √2 with increasing accuracy. The longer the fraction, the closer the approximation gets to the true value.
These methods provide alternative approaches to understanding and working with this fundamental irrational number.
Frequently Asked Questions (FAQ)
Q: Is √2 a rational or irrational number?
A: √2 is an irrational number. This means it cannot be expressed as a fraction of two integers.
Q: What is the approximate value of √2?
A: The approximate value of √2 is 1.41421356...
Q: How is √2 used in geometry?
A: √2 represents the length of the diagonal of a unit square (a square with sides of length 1).
Q: Are there other irrational numbers besides √2?
A: Yes, there are infinitely many irrational numbers. Examples include π (pi), e (Euler's number), and the square root of most integers that are not perfect squares.
Q: Why is the irrationality of √2 important?
A: The discovery of the irrationality of √2 was a significant milestone in the history of mathematics, challenging existing beliefs and expanding the understanding of numbers. It demonstrated the existence of numbers beyond the simple ratios of integers.
Conclusion: The Enduring Legacy of an Irrational Number
The square root of 2, despite its seemingly simple nature, holds a rich history and continues to be relevant across numerous disciplines. Its irrationality challenged foundational mathematical assumptions, pushing the field towards a deeper understanding of numbers and their properties. From its elegant proof by contradiction to its diverse applications in geometry, engineering, and even music, √2 stands as a testament to the power and beauty of mathematics. Its enduring legacy reminds us that even the simplest concepts can hold profound implications and continue to inspire mathematical exploration for generations to come. The seemingly simple √2 reveals the vast and intricate world of numbers, a world where beauty and logic intertwine to reveal the fundamental truths of our universe.
Latest Posts
Latest Posts
-
Map Of Pre Islamic Arabia
Sep 17, 2025
-
Addition And Subtraction To 20
Sep 17, 2025
-
Worksheet On Pronoun Antecedent Agreement
Sep 17, 2025
-
Four Components Of Natural Selection
Sep 17, 2025
-
Convolution Theorem In Laplace Transform
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.