V Pi R 2 H
zacarellano
Sep 21, 2025 · 5 min read
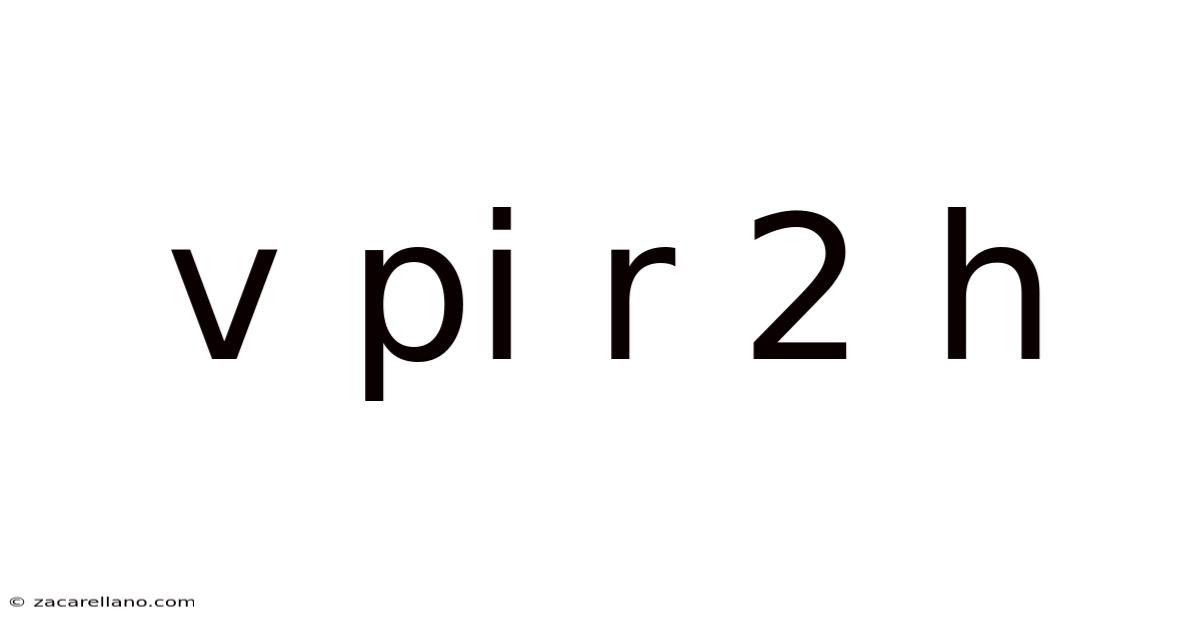
Table of Contents
Understanding the Volume of a Cylinder: V = πr²h
The formula V = πr²h is a cornerstone of geometry, representing the volume of a cylinder. This seemingly simple equation unlocks the ability to calculate the capacity of countless objects, from storage tanks and pipes to cans of soda and even the approximate volume of tree trunks. This article will delve deep into understanding this formula, explaining its components, providing step-by-step calculations, exploring its scientific basis, answering frequently asked questions, and ultimately empowering you to confidently apply this knowledge in various scenarios.
Understanding the Components of the Formula
Before we delve into calculations, let's dissect the formula itself: V = πr²h. Each element plays a crucial role:
-
V: Represents the volume of the cylinder. Volume is the amount of three-dimensional space occupied by an object. In this case, it's the space enclosed within the cylinder's curved surface and circular bases. Volume is typically measured in cubic units, such as cubic centimeters (cm³), cubic meters (m³), or cubic feet (ft³).
-
π (pi): This is a mathematical constant, approximately equal to 3.14159. Pi represents the ratio of a circle's circumference to its diameter. It's an irrational number, meaning its decimal representation goes on forever without repeating. For most practical calculations, using 3.14 or 3.1416 provides sufficient accuracy.
-
r: Represents the radius of the cylinder's circular base. The radius is the distance from the center of the circle to any point on the circle's edge. It's crucial to remember that the formula uses the radius, not the diameter (which is twice the radius).
-
h: Represents the height of the cylinder. This is the perpendicular distance between the two circular bases.
Step-by-Step Calculation of Cylinder Volume
Let's walk through a practical example to solidify our understanding. Imagine we have a cylindrical water tank with a radius of 5 meters and a height of 10 meters. We want to determine its volume.
Step 1: Identify the variables.
- Radius (r) = 5 meters
- Height (h) = 10 meters
- π ≈ 3.1416 (for greater accuracy)
Step 2: Substitute the values into the formula.
V = πr²h = 3.1416 * (5 m)² * (10 m)
Step 3: Perform the calculations.
- Square the radius: (5 m)² = 25 m²
- Multiply by pi: 3.1416 * 25 m² ≈ 78.54 m²
- Multiply by the height: 78.54 m² * 10 m = 785.4 m³
Step 4: State the result.
The volume of the cylindrical water tank is approximately 785.4 cubic meters.
The Scientific Basis: Deriving the Formula
The formula V = πr²h isn't just a memorized equation; it's derived from fundamental geometric principles. Imagine slicing the cylinder into infinitely thin, circular disks. Each disk has a volume approximately equal to the area of its circular base multiplied by its thickness (which is a tiny segment of the height).
The area of a circle is given by the formula A = πr². If we consider the thickness of each disk as a small change in height (Δh), the volume of a single disk is approximately πr²Δh. To find the total volume of the cylinder, we sum up the volumes of all these infinitesimally thin disks. This summation is essentially an integral in calculus, but intuitively, we can see that as Δh approaches zero and the number of disks approaches infinity, the sum becomes the product of the area of the base (πr²) and the total height (h), leading to the formula V = πr²h.
Practical Applications of the Cylinder Volume Formula
The applications of this formula are vast and extend across numerous fields:
-
Engineering: Calculating the volume of pipes, tanks, silos, and other cylindrical structures is crucial for design, construction, and material estimation.
-
Manufacturing: Determining the capacity of cans, containers, and other cylindrical products is essential for packaging and production planning.
-
Environmental Science: Estimating the volume of cylindrical structures in environmental studies, such as tree trunks for biomass calculations or water bodies for hydrological modeling.
-
Medicine: Calculating the volume of cylindrical medical devices or containers for drug storage and delivery.
-
Physics: Understanding the volume of cylindrical objects is crucial for fluid dynamics, heat transfer, and other physical phenomena.
Frequently Asked Questions (FAQ)
Q: What if the cylinder is not perfectly cylindrical?
A: The formula V = πr²h applies only to perfect cylinders. If the cylinder is tapered or has irregular bases, more complex methods involving integral calculus or numerical approximations are needed to calculate the volume.
Q: How do I convert between different units of volume?
A: You can use standard unit conversion factors. For example, to convert cubic meters to cubic centimeters, you would multiply by 1,000,000 (1 m³ = 1,000,000 cm³). Similar conversion factors exist for other unit systems.
Q: Can I use this formula for hollow cylinders?
A: No, this formula calculates the volume of a solid cylinder. For a hollow cylinder, you need to calculate the volume of the outer cylinder and subtract the volume of the inner cylinder.
Q: What if I only know the diameter of the cylinder's base?
A: Remember that the radius (r) is half the diameter (d). So, if you know the diameter, simply divide it by 2 to get the radius, and then proceed with the formula.
Conclusion
Understanding the formula V = πr²h is a fundamental skill with wide-ranging applications. This formula, derived from basic geometric principles and refined through calculus, provides a powerful tool for calculating the volume of cylindrical objects. By mastering this formula and its underlying principles, you unlock the ability to solve numerous practical problems across various disciplines, from everyday tasks to complex engineering projects. Remember to always carefully identify the radius and height, use appropriate units, and choose an accurate value for pi to ensure accurate and reliable results. The seemingly simple equation V = πr²h opens a world of possibilities for understanding and quantifying the three-dimensional space occupied by cylindrical objects.
Latest Posts
Latest Posts
-
Biological Evolution Evidence Unit Test
Sep 21, 2025
-
Dividing By Multiples Of 10
Sep 21, 2025
-
Example Of A Reference Point
Sep 21, 2025
-
1 2 X 1 4
Sep 21, 2025
-
Lewis Dot Diagram For Germanium
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about V Pi R 2 H . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.