V Πr2h Solve For R
zacarellano
Sep 22, 2025 · 5 min read
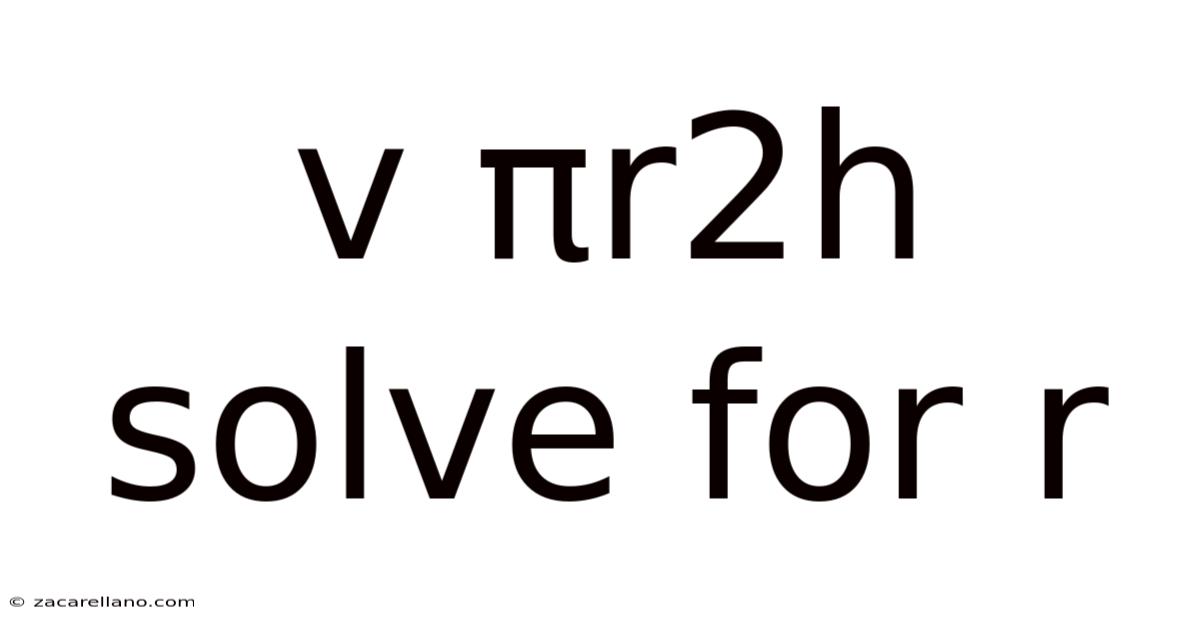
Table of Contents
Solving for the Radius (r) in the Cylinder Volume Formula: V = πr²h
Understanding how to manipulate formulas is a crucial skill in mathematics and science. This article will guide you through the process of solving for the radius (r) in the formula for the volume of a cylinder: V = πr²h. We'll break down the steps, explain the underlying mathematical principles, and address common questions, ensuring you gain a complete understanding of this important concept. This guide is designed for students of all levels, from those just beginning algebra to those looking to reinforce their problem-solving skills. We'll explore not just the mechanical steps but also the reasoning behind each manipulation, empowering you to confidently tackle similar problems in the future.
Understanding the Cylinder Volume Formula
Before diving into solving for r, let's refresh our understanding of the formula itself: V = πr²h. This formula calculates the volume (V) of a right circular cylinder. Let's define each component:
-
V: Represents the volume of the cylinder, typically measured in cubic units (e.g., cubic centimeters, cubic meters). The volume represents the total three-dimensional space enclosed within the cylinder.
-
π (pi): A mathematical constant, approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter and is fundamental in calculating areas and volumes involving circles.
-
r: Represents the radius of the cylinder's circular base. The radius is the distance from the center of the circle to any point on the circle.
-
h: Represents the height of the cylinder. This is the perpendicular distance between the two circular bases.
The formula essentially tells us that the volume of a cylinder is found by multiplying the area of its circular base (πr²) by its height (h).
Step-by-Step Solution: Solving for r
Our goal is to isolate r on one side of the equation. This involves a series of algebraic manipulations, each justified by the properties of equality. Let's break down the process step-by-step:
Step 1: Divide both sides by πh
The first step is to eliminate both π and h from the right-hand side of the equation. Since r is multiplied by both π and h, we can undo these operations by dividing both sides of the equation by πh. This maintains the equality because whatever we do to one side, we must do to the other.
This gives us:
V / (πh) = r²
Step 2: Take the square root of both sides
Now, we have r² isolated. To find r, we need to take the square root of both sides of the equation. Remember that the square root of a number is a value that, when multiplied by itself, equals the original number.
Therefore:
√[V / (πh)] = √r²
This simplifies to:
√[V / (πh)] = r
Step 3: Consider the positive and negative solutions
Mathematically, the square root of a number can be positive or negative. However, in the context of a physical quantity like radius, a negative value doesn't make sense. A cylinder cannot have a negative radius. Therefore, we only consider the positive square root.
Therefore, our final solution is:
r = √[V / (πh)]
This equation allows us to calculate the radius of a cylinder if we know its volume and height.
Illustrative Example
Let's solidify our understanding with a practical example. Suppose we have a cylinder with a volume (V) of 150 cubic centimeters and a height (h) of 10 centimeters. Let's calculate its radius:
-
Substitute the known values: Replace V with 150 and h with 10 in our formula: r = √[150 / (π * 10)]
-
Simplify: This simplifies to r = √[15 / π]
-
Approximate: Using the approximation π ≈ 3.14159, we get: r ≈ √(15 / 3.14159) ≈ √4.7746 ≈ 2.185 cm
Therefore, the radius of the cylinder is approximately 2.185 centimeters.
Mathematical Justification and Properties Used
The solution relies on fundamental algebraic principles:
-
Division Property of Equality: If a = b, then a/c = b/c (as long as c ≠ 0). This justifies dividing both sides by πh.
-
Square Root Property of Equality: If a = b, then √a = √b. This justifies taking the square root of both sides.
-
Simplification: Combining and simplifying terms using the order of operations (PEMDAS/BODMAS).
Frequently Asked Questions (FAQ)
Q1: What if I'm given the diameter instead of the radius?
If you're given the diameter (d), remember that the radius is half the diameter: r = d/2. Substitute this into the volume formula before solving for other variables.
Q2: Can I solve for the height (h) or volume (V) using similar methods?
Absolutely! You can rearrange the formula V = πr²h to solve for h or V using similar algebraic manipulation. To solve for h, divide both sides by πr². To solve for V, simply substitute the known values of r and h into the original formula.
Q3: What if the volume or height is zero?
If either the volume (V) or the height (h) is zero, the cylinder is essentially nonexistent (a cylinder with zero volume or zero height is a flat circle or a line, respectively). The formula will be undefined in these cases because division by zero is not allowed in mathematics.
Q4: How do I handle very large or very small numbers?
For very large or very small numbers, using scientific notation or a calculator with exponential functions can simplify calculations and prevent errors.
Conclusion
Solving for the radius (r) in the cylinder volume formula, V = πr²h, involves a straightforward yet powerful application of algebraic techniques. By systematically applying the division property of equality and the square root property, we can isolate r and determine its value given the volume and height of the cylinder. Understanding this process not only helps in solving this specific problem but also equips you with valuable algebraic skills applicable to a wide range of mathematical and scientific challenges. Remember to always check your work and consider the physical context of your answer – in this case, ensuring the radius is a positive value. Practice with various examples to build your confidence and mastery of this fundamental concept.
Latest Posts
Latest Posts
-
Algebraic Equations With Square Roots
Sep 22, 2025
-
What Enzyme Separates Dna Strands
Sep 22, 2025
-
Where Does Oxaloacetate Come From
Sep 22, 2025
-
Types Of Reproduction Of Bacteria
Sep 22, 2025
-
Heart Rate Negative Feedback Loop
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about V Πr2h Solve For R . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.