What Times 4 Equals 28
zacarellano
Sep 10, 2025 · 5 min read
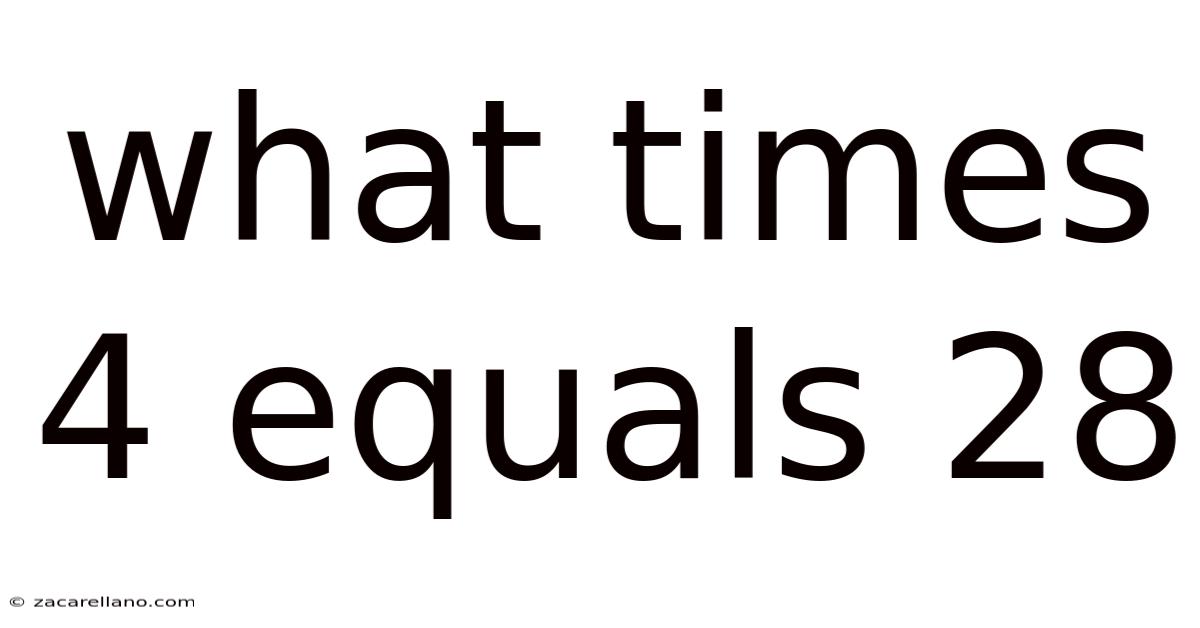
Table of Contents
What Times 4 Equals 28? Unlocking the Mystery of Mathematical Equations
This article delves into the seemingly simple question: "What times 4 equals 28?" While the immediate answer might seem straightforward, exploring this problem opens a door to understanding fundamental mathematical concepts, problem-solving strategies, and even the power of creative thinking. We'll not only find the solution but also unpack the underlying logic, explore different approaches to solving similar problems, and address some common misconceptions.
Introduction: Beyond the Obvious Answer
The quick answer to "What times 4 equals 28?" is 7. Simple multiplication dictates that 7 multiplied by 4 equals 28 (7 x 4 = 28). However, this seemingly basic equation provides a fertile ground for learning and exploration, particularly for those new to mathematics or those looking to reinforce their fundamental skills. This article is designed to go beyond simply providing the answer, aiming instead to deepen your understanding of mathematical reasoning and problem-solving techniques.
Understanding Multiplication: The Building Blocks
Before diving deeper, let's refresh our understanding of multiplication. Multiplication is essentially a shortcut for repeated addition. For example, 7 x 4 can be visualized as adding seven four times: 7 + 7 + 7 + 7 = 28. This concept is crucial, particularly when working with larger numbers or more complex equations. Understanding this fundamental relationship between multiplication and addition allows for a more intuitive grasp of mathematical operations.
Solving the Equation: Different Approaches
While the direct solution (7 x 4 = 28) is clear, let's explore alternative methods to solve similar equations. This will strengthen your mathematical reasoning and broaden your problem-solving toolkit.
-
Division: The inverse operation of multiplication is division. If we know that a number multiplied by 4 equals 28, we can find that number by dividing 28 by 4: 28 ÷ 4 = 7. This approach is particularly useful when the answer isn't immediately obvious.
-
Algebraic Approach: For more complex equations, an algebraic approach is often necessary. We can represent the unknown number with a variable, such as 'x'. The equation then becomes: 4x = 28. To solve for 'x', we divide both sides of the equation by 4: 4x/4 = 28/4, simplifying to x = 7. This method emphasizes the principles of balancing equations, a crucial skill in higher-level mathematics.
-
Visual Representation: For visual learners, a visual representation can be incredibly helpful. Imagine four groups of objects, with seven objects in each group. Counting all the objects would give you a total of 28. This approach is especially effective for younger learners or those who benefit from concrete examples.
Extending the Concept: More Complex Problems
Once you master the basics, you can apply the same principles to solve more complex problems involving multiplication and division. Consider these examples:
-
What times 5 equals 45? Using division, we find 45 ÷ 5 = 9. Therefore, 9 times 5 equals 45.
-
What number multiplied by 8 equals 72? Dividing 72 by 8 gives us 9.
-
If 6 multiplied by a certain number equals 54, what is that number? Solving the equation 6x = 54, by dividing both sides by 6, reveals the answer as 9.
Addressing Common Misconceptions:
-
Order of Operations: Remember the order of operations (PEMDAS/BODMAS) – Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). This is crucial for solving more complex equations.
-
Incorrect Division: A common mistake is incorrectly performing division. Always ensure that you are dividing the correct numbers.
-
Neglecting Units: In real-world applications, always pay attention to units. If you are dealing with measurements (e.g., meters, kilograms), ensure that your units are consistent throughout your calculations.
The Importance of Practice:
Mastering multiplication and division, like any mathematical skill, requires consistent practice. Regularly solving problems of varying difficulty will strengthen your understanding and improve your speed and accuracy. Start with simple problems and gradually increase the complexity as your confidence grows. Utilize resources like worksheets, online quizzes, and educational apps to enhance your learning experience.
Practical Applications:
The ability to solve simple multiplication and division problems like "What times 4 equals 28?" is essential in numerous everyday situations:
-
Shopping: Calculating the total cost of multiple items, determining discounts, and splitting bills with friends all involve basic arithmetic.
-
Cooking: Following recipes often requires scaling ingredients up or down based on the number of servings.
-
Construction and Design: Many construction and design projects rely heavily on precise measurements and calculations.
-
Financial Management: Budgeting, calculating interest, and tracking expenses require a strong understanding of basic arithmetic.
FAQs (Frequently Asked Questions):
-
Q: What if the equation is written differently, such as 4 x ? = 28? A: This is simply a different way of representing the same equation. The question mark represents the unknown number, which can be found by dividing 28 by 4.
-
Q: Are there other ways to solve this equation? A: Yes, you can use visual aids, repeated addition, or even guess-and-check (though this is less efficient for more complex problems).
-
Q: How can I improve my multiplication skills? A: Practice regularly using flashcards, worksheets, online games, and by applying multiplication in real-world scenarios.
Conclusion: More Than Just an Answer
The seemingly simple question "What times 4 equals 28?" serves as a gateway to a deeper understanding of fundamental mathematical principles, problem-solving strategies, and their wide-ranging applications in daily life. By exploring different approaches, addressing potential misconceptions, and engaging in consistent practice, you can not only confidently answer this question but also build a solid foundation for more advanced mathematical concepts. Remember, mathematics is a journey of continuous learning and exploration, and each problem solved brings you one step closer to mastering this essential skill. So, keep practicing, keep exploring, and keep challenging yourself!
Latest Posts
Latest Posts
-
Is Concrete Heterogeneous Or Homogeneous
Sep 10, 2025
-
Organic Chemistry 1 Practice Exam
Sep 10, 2025
-
Ap Physics 2 Unit 1
Sep 10, 2025
-
Prove The Isosceles Triangle Theorem
Sep 10, 2025
-
What Is Perfectly Elastic Collision
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Times 4 Equals 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.