What Times What Equals 18
zacarellano
Sep 25, 2025 · 5 min read
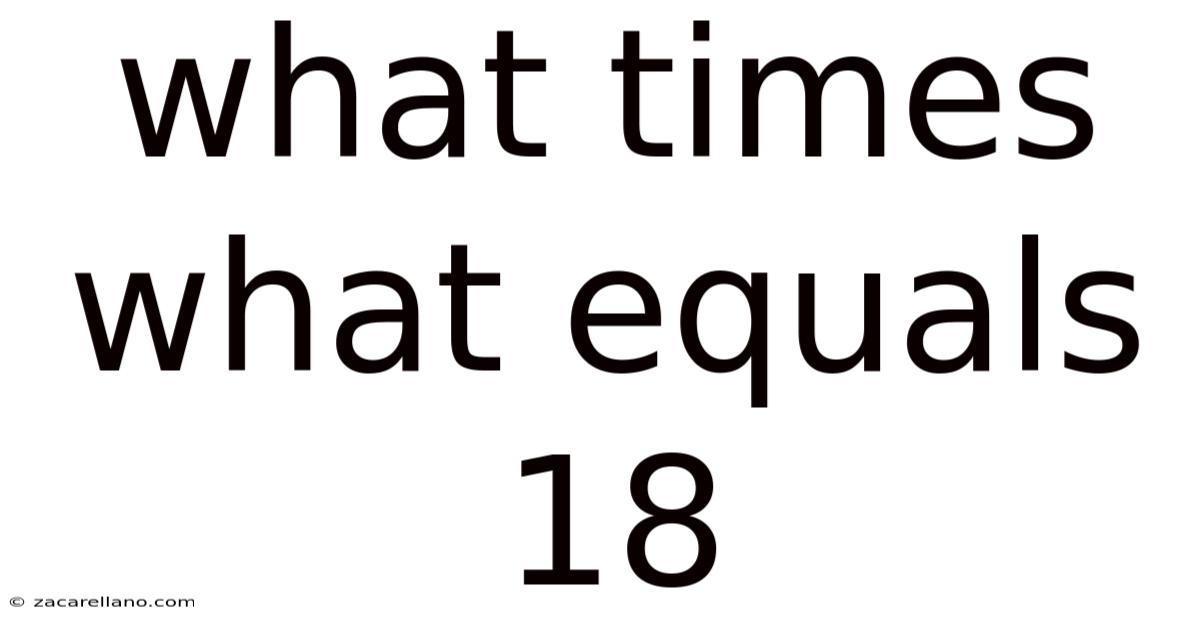
Table of Contents
What Times What Equals 18? Exploring the Factors and Applications of 18
This article delves into the seemingly simple question, "What times what equals 18?" While the answer might seem immediately obvious to some, exploring this question opens up a fascinating journey into the world of factors, prime numbers, and the broader applications of multiplication in mathematics and beyond. We'll not only identify the numerical solutions but also examine the underlying mathematical concepts and real-world examples where understanding factors of 18 proves valuable.
Understanding Factors and Multiplication
Before we dive into the specific factors of 18, let's establish a clear understanding of what factors are. In mathematics, factors are numbers that divide evenly into another number without leaving a remainder. Multiplication is the inverse operation of division; if A x B = C, then A and B are factors of C.
Therefore, the question "What times what equals 18?" is essentially asking us to find the pairs of factors that, when multiplied together, result in the product 18.
Finding the Factor Pairs of 18
Let's systematically list all the factor pairs of 18:
- 1 x 18 = 18 This is the most obvious pair, representing the number itself and 1.
- 2 x 9 = 18 Two is the smallest prime factor of 18, and 9 is its complement in this pair.
- 3 x 6 = 18 Three is another prime factor, paired with 6.
These three pairs (1 and 18, 2 and 9, and 3 and 6) represent all the integer factor pairs of 18. It's crucial to understand that we are focusing on integer factors in this context; we are not considering fractional or decimal solutions.
Prime Factorization of 18
The concept of prime factorization is fundamental in number theory. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Prime factorization involves expressing a number as a product of its prime factors.
Let's perform the prime factorization of 18:
18 can be broken down as 2 x 9. Since 9 is not a prime number (it's divisible by 3), we further break it down: 9 = 3 x 3.
Therefore, the prime factorization of 18 is 2 x 3 x 3, or 2 x 3². This representation is unique to each number and forms the building blocks of the number's properties.
Applications of Understanding Factors of 18
The seemingly simple task of finding the factors of 18 has practical applications across various mathematical fields and real-world scenarios:
-
Algebra: Understanding factors is crucial for simplifying algebraic expressions and solving equations. For instance, factoring quadratic equations relies heavily on identifying factors. Consider the equation x² + 3x -18 = 0. To solve this, you'd need to factor the quadratic expression into (x+6)(x-3) = 0. Understanding the factors of 18 is critical here.
-
Geometry: Calculating the area or volume of shapes often involves multiplication. If a rectangle has a length of 6 units and a width of 3 units, its area is 18 square units. Understanding the factors of 18 helps to visualize different dimensions that could result in the same area.
-
Combinatorics and Probability: When dealing with combinations and permutations, factors help in determining the number of possible arrangements or outcomes. For example, arranging 18 objects in different orders would involve considering its factors in the calculation.
-
Divisibility Rules: The factors of 18 also help illustrate divisibility rules. A number is divisible by 2 if it's an even number. 18 is divisible by 2 because 2 is a factor. It's divisible by 3 because the sum of its digits (1+8=9) is divisible by 3. These divisibility rules provide quick ways to check for factors without performing long division.
-
Real-world Applications: Imagine you have 18 cookies to distribute evenly among friends. Knowing the factors of 18 (1, 2, 3, 6, 9, 18) tells you that you can divide the cookies equally among 1, 2, 3, 6, 9, or 18 friends.
Exploring Beyond Integer Factors
While our primary focus has been on integer factors, it's important to acknowledge that the equation "What times what equals 18?" also has solutions involving non-integer numbers. For example:
- 3/2 x 12 = 18
- 2.25 x 8 = 18
- √18 x √18 = 18
These solutions demonstrate that the problem has a broader set of solutions if we expand beyond the constraints of integer factors. However, in many mathematical contexts, particularly elementary and intermediate algebra, the primary focus remains on integer solutions.
Frequently Asked Questions (FAQ)
-
Q: What are the prime factors of 18?
- A: The prime factors of 18 are 2 and 3 (with 3 appearing twice, i.e., 2 x 3²).
-
Q: Is 18 a composite number?
- A: Yes, 18 is a composite number because it has more than two factors.
-
Q: How many factors does 18 have?
- A: 18 has six factors: 1, 2, 3, 6, 9, and 18.
-
Q: What is the greatest common factor (GCF) of 18 and 24?
- A: To find the GCF, list the factors of both numbers: Factors of 18: 1, 2, 3, 6, 9, 18 Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24 The greatest common factor is 6.
-
Q: What is the least common multiple (LCM) of 18 and 24?
- A: To find the LCM, list the multiples of both numbers: Multiples of 18: 18, 36, 54, 72, 90... Multiples of 24: 24, 48, 72, 96... The least common multiple is 72.
Conclusion
The seemingly simple question, "What times what equals 18?" serves as a gateway to explore fundamental mathematical concepts. From understanding factors and prime factorization to applying these concepts in algebra, geometry, and beyond, this question highlights the interconnectedness of mathematical ideas. The ability to identify the factors of a number, such as 18, is a foundational skill that builds the groundwork for more advanced mathematical problem-solving. The exploration not only provided the numerical answers (1x18, 2x9, 3x6) but also showcased the deeper significance of factors within the broader mathematical landscape. Remember that mathematical understanding is built upon a solid foundation of basic concepts, and mastering these concepts opens the door to a wealth of further exploration and discovery.
Latest Posts
Latest Posts
-
O Que E A Vida
Sep 25, 2025
-
Is Negative Plus Negative Positive
Sep 25, 2025
-
Religion Of The Mauryan Empire
Sep 25, 2025
-
When Do You Use Tangent
Sep 25, 2025
-
Stokes Theorem And Divergence Theorem
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.