Whats Bigger 3/8 Or 1/2
zacarellano
Sep 13, 2025 · 5 min read
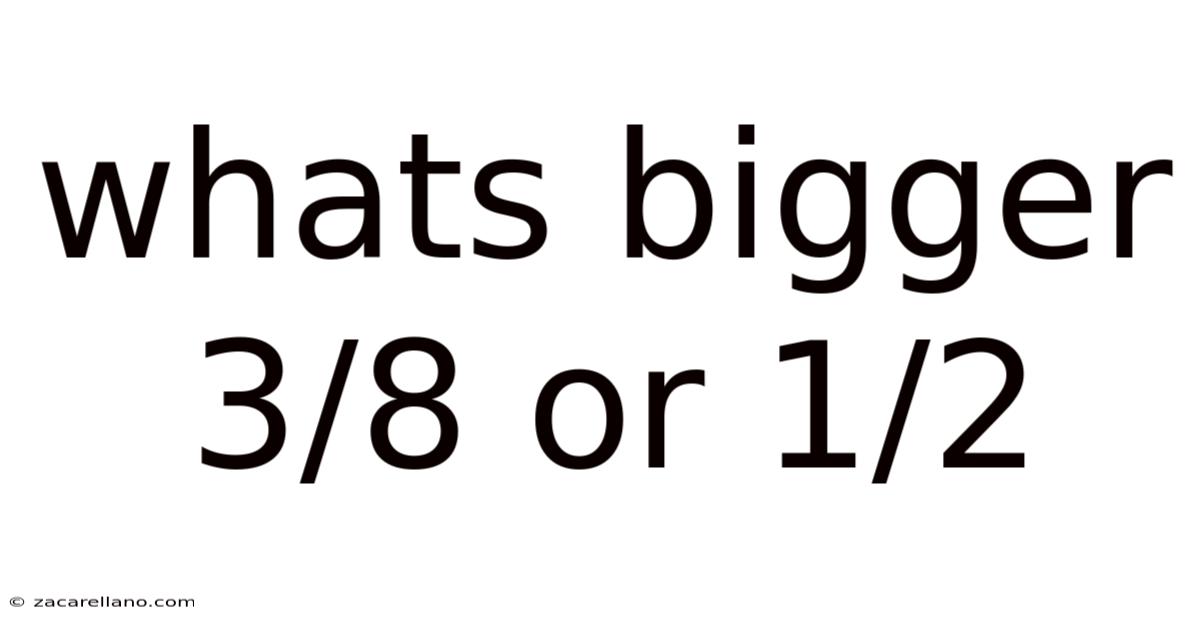
Table of Contents
What's Bigger: 3/8 or 1/2? A Deep Dive into Fraction Comparison
This article explores the seemingly simple question: which is bigger, 3/8 or 1/2? While the answer might seem immediately obvious to some, a deeper understanding of fractions provides valuable insights into mathematical concepts fundamental to numerous fields. We'll not only determine which fraction is larger but also delve into the methods for comparing fractions, exploring various techniques and their applications. This understanding extends beyond simple arithmetic, touching upon concepts crucial for higher-level mathematics and real-world problem-solving.
Understanding Fractions: A Quick Refresher
Before jumping into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we have 3 out of 8 equal parts of a whole. Similarly, 1/2 represents 1 out of 2 equal parts.
Comparing 3/8 and 1/2: Three Methods
There are several ways to compare 3/8 and 1/2 to determine which is larger. Let's examine three common methods:
Method 1: Finding a Common Denominator
This is arguably the most straightforward and widely used method. The core principle is to rewrite both fractions with the same denominator. The least common denominator (LCD) is the smallest multiple that both denominators share.
In our case, the denominators are 8 and 2. The multiples of 2 are 2, 4, 6, 8, 10… and the multiples of 8 are 8, 16, 24… The least common multiple (and therefore the LCD) is 8.
- Converting 1/2: To change the denominator of 1/2 to 8, we multiply both the numerator and the denominator by 4 (because 2 x 4 = 8): (1 x 4) / (2 x 4) = 4/8
Now we can easily compare:
- 3/8 and 4/8
Since both fractions now have the same denominator, we can compare the numerators directly. 4 is greater than 3, therefore:
4/8 > 3/8, meaning 1/2 > 3/8
Method 2: Converting to Decimals
Another effective method involves converting both fractions into their decimal equivalents. This method is particularly useful when dealing with more complex fractions or when working with calculators.
-
Converting 3/8 to a decimal: Divide the numerator (3) by the denominator (8): 3 ÷ 8 = 0.375
-
Converting 1/2 to a decimal: Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
Now we compare the decimal values:
0.5 > 0.375, therefore 1/2 > 3/8
Method 3: Visual Representation
This method is excellent for visualizing the comparison, particularly for beginners. Imagine two identical circles or rectangles.
-
Representing 1/2: Divide the first shape into two equal halves and shade one half.
-
Representing 3/8: Divide the second shape into eight equal parts and shade three of them.
Visually inspecting the shaded areas clearly demonstrates that the shaded area representing 1/2 is larger than the shaded area representing 3/8.
Expanding the Understanding: Beyond Simple Comparison
While the comparison of 3/8 and 1/2 is relatively simple, the underlying principles extend to more complex scenarios. Understanding fraction comparison is crucial for:
-
Solving Equations: Many algebraic equations involve fractions, and the ability to compare and manipulate fractions is essential for solving them.
-
Data Analysis: In statistics and data analysis, fractions and percentages (which are essentially fractions with a denominator of 100) are frequently used to represent proportions and probabilities. Comparing fractions is vital for interpreting and analyzing data accurately.
-
Geometry and Measurement: In geometry, fractions are used extensively to represent lengths, areas, and volumes. Comparing fractions is necessary for determining relative sizes and proportions of geometrical figures.
-
Real-World Applications: Fractions are ubiquitous in everyday life, from cooking recipes (e.g., 1/2 cup of sugar) to calculating discounts and proportions in various situations. The ability to compare and manipulate fractions is a highly practical skill.
Further Exploring Fraction Operations
Beyond comparison, understanding other fraction operations is crucial:
-
Addition and Subtraction: To add or subtract fractions, you must have a common denominator. Once you have a common denominator, you simply add or subtract the numerators and keep the denominator the same.
-
Multiplication: Multiplying fractions is simpler. Multiply the numerators together and multiply the denominators together.
-
Division: To divide fractions, you invert the second fraction (reciprocal) and then multiply.
Frequently Asked Questions (FAQ)
Q1: Is there a quicker way to compare fractions without finding a common denominator or converting to decimals?
A1: While finding a common denominator or converting to decimals are reliable methods, sometimes you can make a quick judgment based on the relative sizes of the numerators and denominators. For example, if you have 3/8 and 1/2, you can intuitively see that 1/2 is closer to a whole than 3/8 is. However, this method is not always reliable and should be used cautiously for more complex comparisons.
Q2: How do I compare fractions with different denominators and numerators that are not easily converted?
A2: For more complex fractions, finding the least common denominator remains the most reliable method. Alternatively, converting to decimals provides a consistent and accurate comparison.
Q3: Why is understanding fraction comparison important in higher-level mathematics?
A3: Fraction comparison is a fundamental building block for numerous advanced mathematical concepts. It's crucial for working with rational numbers, solving equations involving fractions, understanding ratios and proportions, and many other topics in algebra, calculus, and beyond.
Q4: Are there any online tools or resources to help with fraction comparison?
A4: While I cannot provide specific links to external websites, many online calculators and educational websites offer tools for comparing fractions, converting fractions to decimals, and performing other fraction operations. A quick search online will uncover numerous helpful resources.
Conclusion
In conclusion, 1/2 is definitively larger than 3/8. However, the significance of this simple comparison extends far beyond the answer itself. Understanding the various methods for comparing fractions – finding a common denominator, converting to decimals, and even visual representation – lays a solid foundation for more complex mathematical concepts and real-world problem-solving. The ability to comfortably manipulate and compare fractions is a crucial skill that extends beyond the classroom and into countless applications in everyday life and professional fields. Mastering this skill unlocks a deeper understanding of mathematics and empowers you to tackle more intricate problems with confidence.
Latest Posts
Latest Posts
-
Current Divider And Voltage Divider
Sep 13, 2025
-
Volume Of A Pyramid Problems
Sep 13, 2025
-
Forma Desarrollada De Los Numeros
Sep 13, 2025
-
Sinal De Maior E Menor
Sep 13, 2025
-
World War I Total War
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Whats Bigger 3/8 Or 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.