Why Does 1x1 Equal 1
zacarellano
Sep 22, 2025 · 6 min read
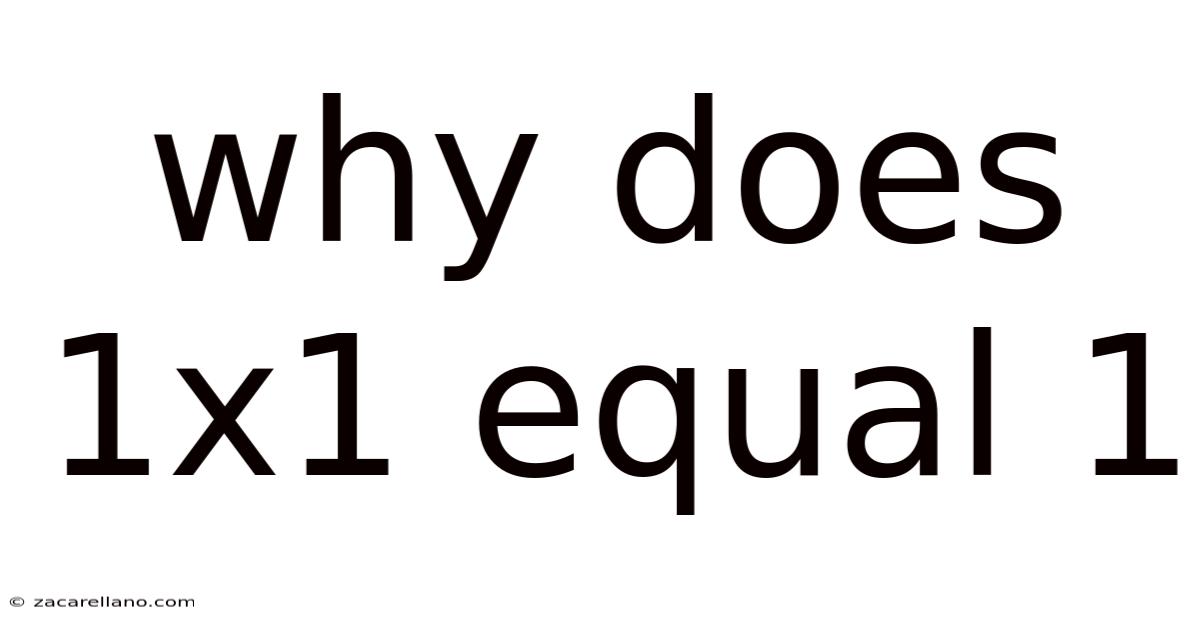
Table of Contents
Why Does 1 x 1 = 1? Unpacking the Fundamentals of Multiplication
The seemingly simple equation, 1 x 1 = 1, is actually a cornerstone of mathematics. While it might appear self-evident to many, understanding why this equation holds true delves into the fundamental principles of multiplication and number systems. This exploration will not only explain the equation itself but also shed light on the broader concepts it represents, including the multiplicative identity and the nature of the operation of multiplication.
Introduction: Multiplication as Repeated Addition
Before diving into the specifics of 1 x 1, let's establish a basic understanding of multiplication. At its core, multiplication is a shorthand way of performing repeated addition. For example, 3 x 2 means adding 2 to itself three times: 2 + 2 + 2 = 6. Similarly, 5 x 4 means adding 4 to itself five times: 4 + 4 + 4 + 4 + 4 = 20. This foundational understanding is crucial for grasping why 1 x 1 = 1.
Understanding 1 x 1: The Multiplicative Identity
Applying the repeated addition concept to 1 x 1, we would add 1 to itself one time: 1. This straightforward calculation leads us to the answer: 1 x 1 = 1. However, this is just one perspective. A deeper understanding involves the concept of the multiplicative identity.
In mathematics, the multiplicative identity is the number that, when multiplied by any other number, leaves that number unchanged. This number is 1. This property is expressed as: a x 1 = a and 1 x a = a, where a can be any number. Therefore, when we multiply 1 by 1, we are applying this property. The result, as defined by the multiplicative identity, remains 1.
The Role of Sets and Number Systems
We can also visualize 1 x 1 using the concept of sets. In set theory, multiplication can be interpreted as finding the number of elements in the Cartesian product of two sets. If we have a set A with one element (let's say A = {1}) and a set B with one element (B = {1}), the Cartesian product A x B is {(1,1)}. This Cartesian product contains only one ordered pair, thus illustrating that 1 x 1 = 1.
Beyond Repeated Addition: Exploring Other Perspectives
While repeated addition provides an intuitive approach for understanding multiplication, especially for larger numbers, it's less intuitive for 1 x 1. Let's explore some alternative perspectives that solidify our understanding:
-
The Area Model: Imagine a square with sides of length 1 unit. The area of this square is calculated by multiplying the length by the width: 1 unit x 1 unit = 1 square unit. This geometrical interpretation visually demonstrates that 1 x 1 = 1.
-
Abstract Algebra: In abstract algebra, multiplication is defined through axioms and properties. The multiplicative identity is a fundamental axiom within these systems, guaranteeing that 1 x 1 = 1. These systems provide a rigorous and abstract framework for defining mathematical operations and their properties. The consistency of these axioms ensures the validity of 1 x 1 = 1 across various mathematical structures.
-
Number Lines and Transformations: Consider a number line. Multiplication by 1 can be interpreted as a transformation that leaves every point on the number line unchanged. Multiplying 1 by 1 simply means applying this identity transformation to the point 1, resulting in the point 1 remaining unchanged. This perspective emphasizes the role of 1 as a neutral element under multiplication.
Addressing Potential Misconceptions
While 1 x 1 = 1 is a straightforward concept, some students might encounter misconceptions. These often stem from a lack of understanding of the fundamental principles of multiplication and the role of the multiplicative identity.
-
Confusing Multiplication with Addition: Students might mistakenly try to add the numbers rather than multiply them. Reinforcing the concept of repeated addition as the basis for multiplication can help address this misconception.
-
Overlooking the Multiplicative Identity: A thorough understanding of the multiplicative identity is critical. Explicitly highlighting the role of 1 as the number that leaves any other number unchanged under multiplication is crucial.
-
Lack of Visual Representation: Using visual aids like the area model can be extremely helpful in clarifying the concept, especially for visual learners.
Practical Applications and Importance
Understanding 1 x 1 = 1 isn't just about memorizing a simple fact; it's foundational to numerous mathematical concepts and applications:
-
Algebra: The multiplicative identity is crucial in simplifying algebraic expressions and solving equations. Understanding this property helps in manipulating equations and finding solutions efficiently.
-
Calculus: The concept of limits and derivatives relies heavily on the properties of multiplication, including the multiplicative identity.
-
Computer Science: In programming, the multiplicative identity is essential in various algorithms and data structures. Understanding its properties ensures correct program execution.
-
Real-World Applications: Many real-world problems involve multiplication, and understanding the fundamental principles allows for accurate calculations in areas like finance, engineering, and science.
Frequently Asked Questions (FAQs)
-
Q: Is there any instance where 1 x 1 does not equal 1?
- A: No, within standard number systems (real numbers, complex numbers, etc.), 1 x 1 always equals 1. This is a fundamental axiom that forms the basis of mathematical operations.
-
Q: Why is it important to understand why 1 x 1 = 1?
- A: Understanding why this equation is true goes beyond simple memorization. It strengthens the foundational understanding of multiplication, the multiplicative identity, and its broader implications in more advanced mathematical concepts.
-
Q: How can I help children understand 1 x 1 = 1?
- A: Use visual aids like blocks or drawings to represent the concept of repeated addition. Explain the multiplicative identity in simple terms. Relate the equation to real-world examples, like having one group of one item.
-
Q: Is there any exception to the multiplicative identity property?
- A: In certain abstract algebraic structures (like modulo arithmetic), the multiplicative identity might be different from 1, but even in these cases, the concept of a multiplicative identity remains vital.
Conclusion: A Foundation of Mathematical Understanding
The equation 1 x 1 = 1, while seemingly trivial, encapsulates fundamental principles within mathematics. Understanding this equation involves comprehending the nature of multiplication, the role of the multiplicative identity, and its significance in various mathematical fields and applications. Mastering this basic concept lays a strong foundation for progressing to more complex mathematical ideas and problem-solving. By exploring different perspectives and addressing potential misconceptions, we can gain a deeper appreciation for the elegance and power of this seemingly simple yet crucial mathematical truth. The seemingly simple act of multiplying one by one is not merely a calculation; it is a demonstration of fundamental mathematical laws that underpin a vast landscape of mathematical concepts and applications.
Latest Posts
Latest Posts
-
Que Es Una Mezcla Heterogenea
Sep 22, 2025
-
Deadweight Loss Price Ceiling Graph
Sep 22, 2025
-
Great Barrier Reef Abiotic Factors
Sep 22, 2025
-
Position Vs Time Squared Graph
Sep 22, 2025
-
Conditions Of A Perfect Market
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Why Does 1x1 Equal 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.