X 2 5 X 2
zacarellano
Sep 10, 2025 · 6 min read
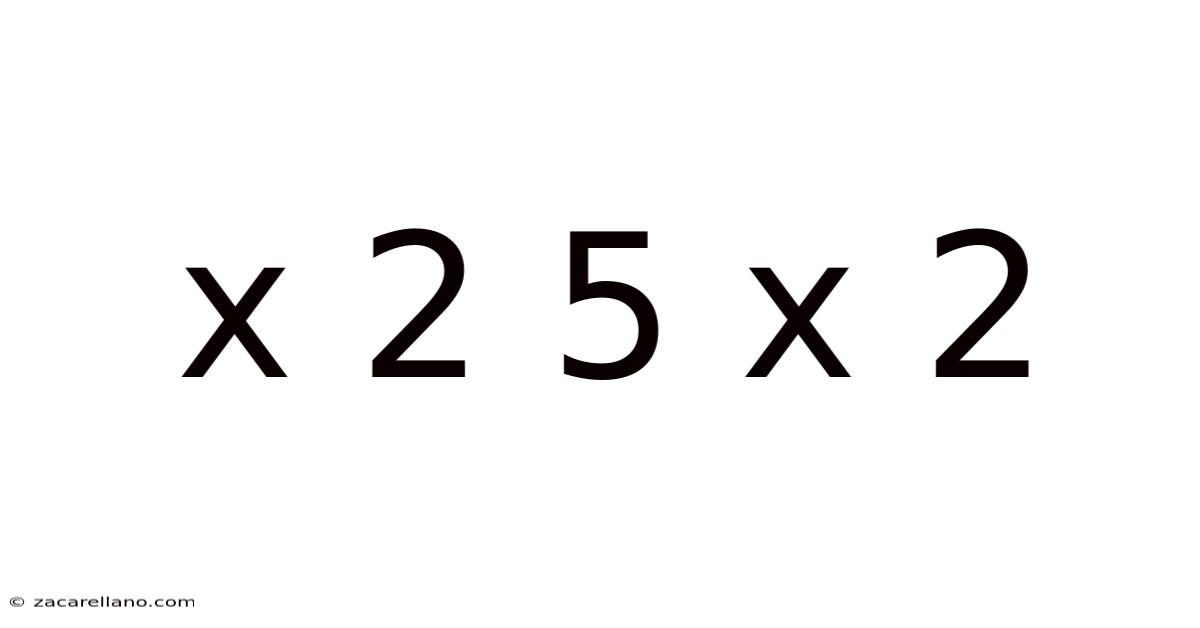
Table of Contents
Decoding the Enigma: A Deep Dive into x² + 5x + 2
This article explores the quadratic expression x² + 5x + 2, delving into its various facets, from basic understanding to advanced applications. We will cover methods for solving, analyzing its properties, graphing it, and even exploring its real-world applications. Whether you're a high school student grappling with algebra or a math enthusiast looking to refresh your knowledge, this comprehensive guide will provide a solid understanding of this seemingly simple yet profoundly rich mathematical concept. This exploration will cover factoring, the quadratic formula, completing the square, graphing techniques, and the discriminant’s role in understanding the nature of the roots.
Understanding Quadratic Expressions
Before diving into the specifics of x² + 5x + 2, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and 'a' is not equal to zero. Our expression, x² + 5x + 2, fits this form perfectly, with a = 1, b = 5, and c = 2.
Understanding this standard form is crucial because it allows us to apply various techniques to solve for x, analyze its properties, and visualize it graphically.
Solving for x: Different Approaches
Finding the values of x that satisfy the equation x² + 5x + 2 = 0 is the core of solving this quadratic expression. Several methods achieve this, each with its own advantages and disadvantages.
1. Factoring
Factoring is a method of expressing the quadratic expression as a product of two simpler expressions. Unfortunately, x² + 5x + 2 doesn't factor easily using integers. While some quadratic expressions can be quickly factored by inspection, this one requires more advanced techniques or alternative methods.
2. The Quadratic Formula
The quadratic formula is a powerful tool that works for all quadratic equations, regardless of whether they factor easily. It's derived from completing the square (discussed below) and provides a direct solution. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in the values from our expression (a = 1, b = 5, c = 2), we get:
x = [-5 ± √(5² - 4 * 1 * 2)] / 2 * 1 x = [-5 ± √(25 - 8)] / 2 x = [-5 ± √17] / 2
This gives us two solutions:
x₁ = (-5 + √17) / 2 ≈ -0.438 x₂ = (-5 - √17) / 2 ≈ -4.562
These are the roots or zeros of the quadratic equation. They represent the x-intercepts of the parabola when graphed.
3. Completing the Square
Completing the square is a technique used to manipulate the quadratic expression into a perfect square trinomial, making it easier to solve. The process involves manipulating the equation to resemble (x + p)² = q, where p and q are constants.
- Move the constant term to the right side: x² + 5x = -2
- Take half of the coefficient of x (5), square it ((5/2)² = 6.25), and add it to both sides: x² + 5x + 6.25 = -2 + 6.25
- Factor the left side as a perfect square: (x + 2.5)² = 4.25
- Take the square root of both sides: x + 2.5 = ±√4.25
- Solve for x: x = -2.5 ± √4.25
This method leads to the same solutions as the quadratic formula, albeit with a slightly different approach. It's particularly useful for understanding the vertex form of a parabola.
Graphing the Quadratic Expression
Visualizing the quadratic expression x² + 5x + 2 as a parabola is insightful. The parabola's shape, vertex, and intercepts provide a comprehensive understanding of the expression's behavior.
-
Vertex: The vertex represents the minimum or maximum point of the parabola. For a quadratic in the form ax² + bx + c, the x-coordinate of the vertex is given by -b/2a. In our case, it's -5/(2*1) = -2.5. Substituting this back into the equation gives the y-coordinate: (-2.5)² + 5(-2.5) + 2 = -4.25. Therefore, the vertex is (-2.5, -4.25).
-
x-intercepts: These are the points where the parabola intersects the x-axis, representing the roots we calculated earlier using the quadratic formula: approximately -0.438 and -4.562.
-
y-intercept: The y-intercept is the point where the parabola intersects the y-axis. This occurs when x = 0. Substituting x = 0 into the equation gives y = 2. The y-intercept is (0, 2).
By plotting these points and sketching a smooth curve, we can visualize the parabola. The parabola opens upwards because the coefficient of x² (a = 1) is positive.
The Discriminant: Understanding the Nature of Roots
The discriminant (b² - 4ac) within the quadratic formula provides valuable information about the nature of the roots (solutions) without directly solving the equation.
-
b² - 4ac > 0: The quadratic equation has two distinct real roots. This is the case for x² + 5x + 2 (17 > 0). The parabola intersects the x-axis at two distinct points.
-
b² - 4ac = 0: The quadratic equation has one real root (a repeated root). The parabola touches the x-axis at exactly one point.
-
b² - 4ac < 0: The quadratic equation has no real roots. The parabola does not intersect the x-axis; its roots are complex numbers (involving the imaginary unit i).
Applications of Quadratic Equations
Quadratic equations are not merely abstract mathematical concepts; they have wide-ranging applications in various fields. A few examples include:
-
Physics: Projectile motion, where the trajectory of an object under gravity is described by a quadratic equation.
-
Engineering: Designing bridges, arches, and other structures where the parabolic shape is crucial for structural integrity.
-
Economics: Modeling supply and demand curves, optimization problems, and growth/decay scenarios.
-
Computer Graphics: Creating curved lines and shapes, essential for rendering realistic images.
Frequently Asked Questions (FAQ)
Q1: Can all quadratic equations be solved by factoring?
No, not all quadratic equations can be easily factored using integers. The quadratic formula or completing the square provides more general solutions.
Q2: What does it mean if the discriminant is negative?
A negative discriminant indicates that the quadratic equation has no real roots. The roots are complex numbers, involving the imaginary unit i.
Q3: How can I check if my solutions are correct?
Substitute the calculated values of x back into the original equation (x² + 5x + 2 = 0). If the equation holds true, your solutions are correct.
Q4: What is the significance of the vertex of a parabola?
The vertex represents the minimum (if the parabola opens upwards) or maximum (if it opens downwards) value of the quadratic function. It's crucial in optimization problems.
Conclusion
The seemingly simple quadratic expression x² + 5x + 2 holds a wealth of mathematical richness. Through factoring, the quadratic formula, completing the square, and graphical analysis, we’ve explored its solutions, properties, and applications. Understanding the discriminant allows us to quickly determine the nature of the roots without explicitly solving the equation. This detailed exploration highlights the power and versatility of quadratic equations within mathematics and its diverse applications in the real world. Mastering these concepts lays a strong foundation for tackling more complex mathematical challenges in the future. Remember to practice regularly, and you’ll soon find yourself confidently solving quadratic equations and appreciating their elegance and practicality.
Latest Posts
Latest Posts
-
Who Brought Christianity To America
Sep 10, 2025
-
Negative 5 Minus Negative 2
Sep 10, 2025
-
Lcm Of 24 And 32
Sep 10, 2025
-
Is There Actin In Mitochondria
Sep 10, 2025
-
Definition Of Absorption In Physics
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about X 2 5 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.