X 2 X 5 Simplify
zacarellano
Sep 13, 2025 · 5 min read
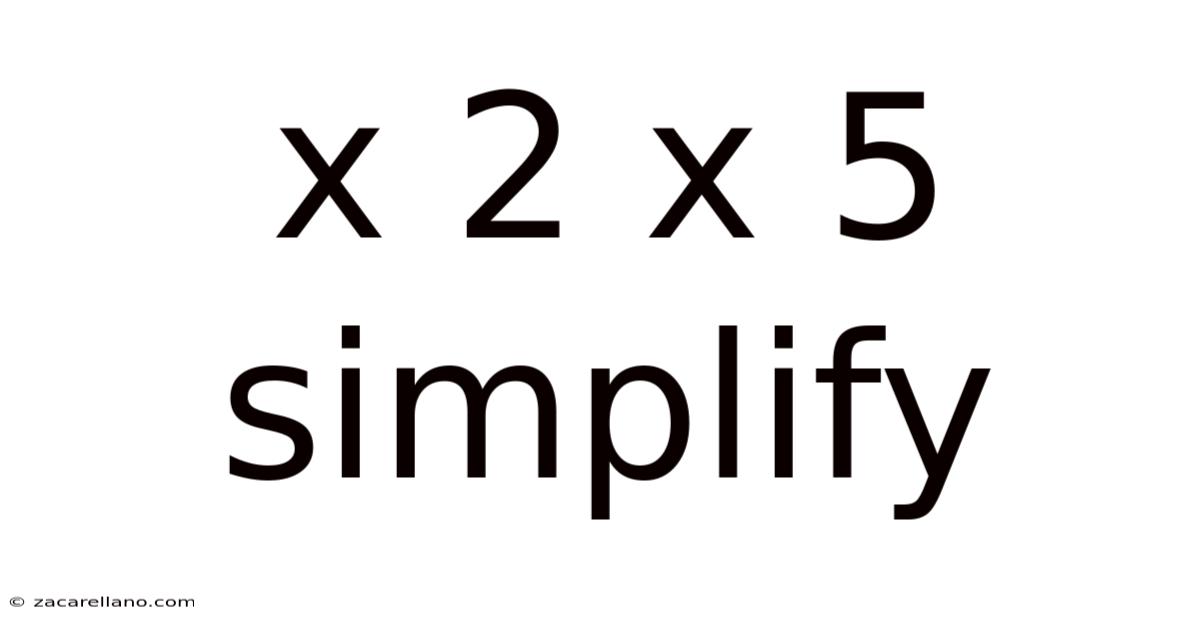
Table of Contents
Mastering Simplification: A Deep Dive into x² x 5
Understanding how to simplify algebraic expressions is a fundamental skill in mathematics. This article will provide a comprehensive guide to simplifying the expression "x² x 5," covering not only the straightforward solution but also exploring the underlying principles and expanding upon related concepts. We'll delve into the rules of exponents, the commutative property, and even touch upon more complex scenarios to solidify your understanding. By the end, you'll be confident in simplifying similar expressions and have a deeper grasp of algebraic manipulation.
Introduction: Understanding the Basics
The expression "x² x 5" involves two core mathematical components: a variable (x) raised to a power (²) and a constant (5). Simplifying means expressing this in the most concise and efficient form possible. This seemingly simple expression offers a perfect opportunity to illustrate several crucial algebraic concepts. We will dissect the process step-by-step, explaining the reasoning behind each operation.
Step-by-Step Simplification: x² x 5
The simplification process hinges on the understanding of the commutative and associative properties of multiplication. These properties allow us to rearrange and group terms without altering the result.
-
Commutative Property: The commutative property of multiplication states that the order of factors does not affect the product. In other words, a x b = b x a. Therefore, we can rewrite our expression as: 5 x x²
-
Associative Property: The associative property of multiplication states that the grouping of factors does not affect the product. In other words, (a x b) x c = a x (b x c). While not explicitly applied here in a visually obvious way, this property underpins the very nature of multiplication and allows us to proceed with the next step.
-
Combining the Constant and Variable: Now, we combine the constant (5) with the variable term (x²). Since multiplication is implied, we simply write: 5x²
Therefore, the simplified form of x² x 5 is 5x².
Explanation of the Rules: Exponents and Coefficients
Let's break down the components to fully grasp the simplification.
-
Coefficients: The number 5 in our expression is called the coefficient. A coefficient is a numerical factor that multiplies a variable. In this case, 5 is the coefficient of x².
-
Variables: The letter 'x' represents a variable. A variable is a symbol (usually a letter) that can represent any number.
-
Exponents: The superscript '2' in x² is an exponent. An exponent indicates how many times a base is multiplied by itself. In x², 'x' is the base, and '2' indicates that x is multiplied by itself (x * x). This is also known as x squared.
The simplification didn't change the exponent because we were only multiplying, not adding or subtracting terms with the same base and different exponents. If we had x² + x², we would have simplified that to 2x², demonstrating the addition of like terms.
Expanding the Concept: More Complex Scenarios
Let's explore more intricate examples to solidify your understanding of simplification.
Scenario 1: 3x³ x 2x⁴
This involves both coefficients and variables with exponents.
-
Rearrange: Use the commutative property to group the coefficients and variables separately: (3 x 2) x (x³ x x⁴)
-
Multiply Coefficients: 3 x 2 = 6
-
Multiply Variables: When multiplying variables with the same base and different exponents, we add the exponents: x³ x x⁴ = x⁽³⁺⁴⁾ = x⁷
-
Combine: Combine the results: 6x⁷
Therefore, 3x³ x 2x⁴ simplifies to 6x⁷.
Scenario 2: (2x²)² x 5x
This introduces the concept of exponents of exponents.
-
Expand the Power: First, address the (2x²)² term. Remember that (ab)² = a²b². Applying this, we get (2²) x (x²)² = 4x⁴
-
Rewrite: The expression is now 4x⁴ x 5x
-
Simplify: Follow the same steps as previous examples: (4 x 5) x (x⁴ x x) = 20x⁵
Therefore, (2x²)² x 5x simplifies to 20x⁵.
Scenario 3: Involving Subtraction:
While the initial example focused solely on multiplication, it's crucial to understand how to approach situations involving subtraction (or addition) of like terms. For example: 3x² + 5x² - 2x²
The coefficients are combined, but the variables remain unchanged. 3 + 5 - 2 = 6. Therefore the answer is 6x²
This highlights that simplification depends on whether the terms are being added, subtracted, or multiplied. It emphasizes the importance of understanding like terms—terms with the same variables raised to the same power. Only like terms can be combined through addition or subtraction.
Frequently Asked Questions (FAQ)
-
Q: What if the expression involved division instead of multiplication?
A: When dividing variables with the same base, you subtract the exponents. For example, x⁵ / x² = x⁽⁵⁻²⁾ = x³. Similarly, coefficients are divided as normal numbers. For example, 6x⁵ / 2x² = 3x³.
-
Q: What happens if the exponents are negative?
A: Negative exponents represent reciprocals. For instance, x⁻² = 1/x². The rules for multiplication and division of exponents still apply.
-
Q: Can I simplify expressions with multiple variables?
A: Yes, absolutely. You'll apply the same principles, grouping like terms and combining coefficients. For example, simplifying 3xy² x 2x²y would involve: (3 x 2) x (x x x²) x (y² x y) = 6x³y³.
-
Q: What if I have a mix of addition, subtraction and multiplication?
A: Remember the order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). This dictates the order in which you perform the calculations.
Conclusion: Mastering Algebraic Simplification
Simplifying algebraic expressions like x² x 5 is a cornerstone of algebra. Understanding the commutative and associative properties, along with the rules of exponents and coefficients, allows you to efficiently manipulate expressions and solve more complex problems. The examples provided demonstrate how to systematically simplify expressions, regardless of their complexity. Remember to always follow the order of operations and focus on combining like terms, and you'll be well on your way to mastering algebraic simplification. Practice is key – the more you work through these types of problems, the more intuitive the process will become. Don't hesitate to tackle more challenging examples to further solidify your skills and confidence.
Latest Posts
Latest Posts
-
8th Grade Math Standards Nc
Sep 13, 2025
-
Is Cholesterol Hydrophobic Or Hydrophilic
Sep 13, 2025
-
Diagram Of The Atp Adp Cycle
Sep 13, 2025
-
Ap Bio Unit 7 Mcq
Sep 13, 2025
-
Are Covaent Xompounds Eletrically Charged
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 5 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.