X 3 8 X 2
zacarellano
Sep 22, 2025 · 6 min read
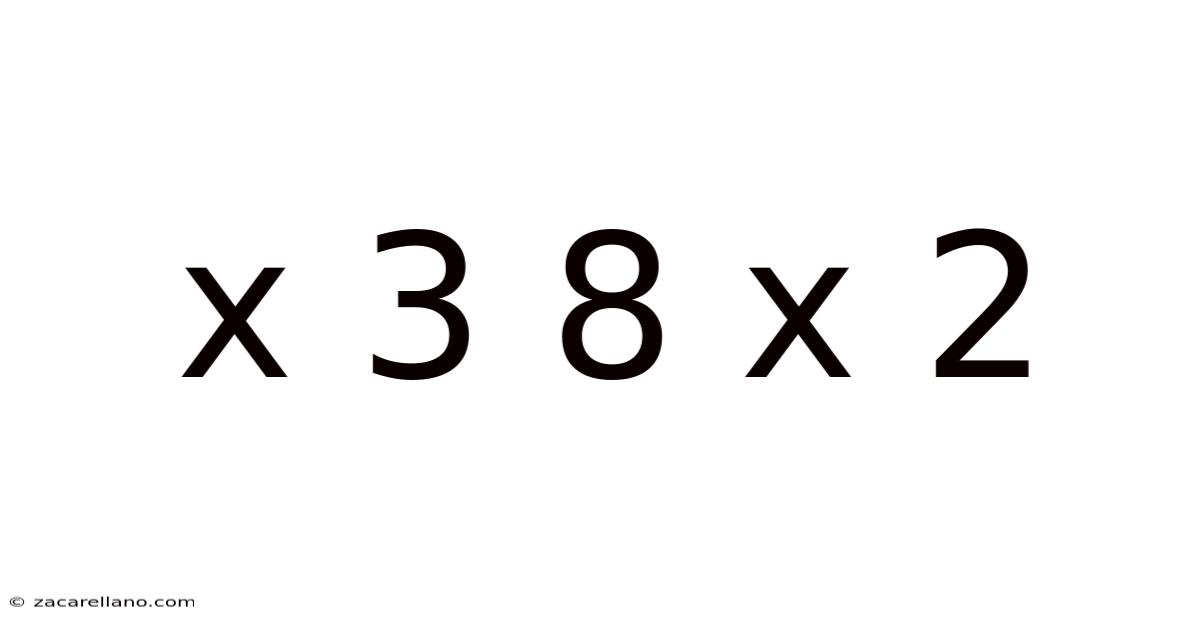
Table of Contents
Decoding the Mystery: Exploring the Mathematical Possibilities of "x 3 8 x 2"
This article delves into the intriguing mathematical puzzle presented by "x 3 8 x 2". At first glance, it seems simple, yet it opens a door to a fascinating exploration of algebra, order of operations, potential solutions, and the importance of clear mathematical notation. We'll unravel the different interpretations, discuss the methods to solve them, and explore the broader mathematical concepts this seemingly simple expression highlights.
Understanding the Ambiguity: Why "x 3 8 x 2" is Not Straightforward
The primary challenge with "x 3 8 x 2" lies in its ambiguous nature. The absence of parentheses or other clarifying symbols leaves room for multiple interpretations. This ambiguity isn't a flaw; it's an excellent opportunity to understand the crucial role of proper mathematical notation in preventing misinterpretations and ensuring clear communication. Without explicit grouping, the order in which we perform the operations significantly affects the final result.
Potential Interpretations and Solutions
Let's explore the possible interpretations of "x 3 8 x 2" and their respective solutions. We'll use the standard order of operations, often remembered by the acronym PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). However, the absence of parentheses forces us to rely on the left-to-right rule for multiplication.
Interpretation 1: (x * 3) * 8 * 2
This interpretation follows a strict left-to-right approach. We perform the multiplication sequentially:
- x * 3 = 3x
- 3x * 8 = 24x
- 24x * 2 = 48x
Therefore, in this interpretation, the solution is 48x. This represents a linear expression where the final result is a multiple of the unknown variable 'x'.
Interpretation 2: x * (3 * 8) * 2
Here, we prioritize the multiplication within the implied grouping suggested by the proximity of '3' and '8':
- 3 * 8 = 24
- x * 24 = 24x
- 24x * 2 = 48x
Surprisingly, even with this different grouping, we arrive at the same solution: 48x. This highlights that in certain situations, different order of operations may lead to the same outcome.
Interpretation 3: x * 3 * (8 * 2)
In this case, we group the '8' and '2' together:
- 8 * 2 = 16
- x * 3 = 3x
- 3x * 16 = 48x
Again, the solution remains 48x. This reinforces the idea that the absence of parentheses, while ambiguous, doesn't necessarily lead to drastically different solutions in this specific example due to the commutative property of multiplication.
Interpretation 4: Considering Implicit Parentheses and Context
While the mathematical expression is ambiguous, real-world contexts could provide implicit grouping. For instance, if this expression arose from a geometric problem, the grouping might be subtly implied by the context of the problem. Imagine a rectangular prism with dimensions 'x', '3', '8', and you need to calculate the volume multiplied by 2. This might lead to an interpretation like (x * 3 * 8) * 2, resulting in 48x.
The Importance of Clear Notation: Avoiding Ambiguity
The exercise with "x 3 8 x 2" underscores the critical role of clear mathematical notation. Ambiguity can lead to misinterpretations, errors, and wasted time. It emphasizes the importance of using parentheses, brackets, and other grouping symbols to explicitly define the order of operations. This is crucial not only in simple expressions but especially in more complex equations and formulas where even a small error in interpretation can lead to vastly different outcomes.
Expanding the Discussion: Algebraic Manipulation and Solving for x
While we've explored various interpretations of the expression, it's important to remember that we haven't 'solved' for 'x'. The solutions we've obtained are all expressions containing 'x'. To solve for 'x', we need an equation – a statement that equates two expressions. For example:
- 48x = 96
In this case, we can solve for 'x' by dividing both sides of the equation by 48:
- x = 96 / 48 = 2
This demonstrates that the expression "x 3 8 x 2" only provides part of the puzzle; a complete equation is necessary to determine a numerical value for 'x'.
Exploring Related Concepts: Order of Operations and the Commutative Property
This simple expression serves as a gateway to deeper mathematical concepts:
-
Order of Operations (PEMDAS/BODMAS): This fundamental principle dictates the sequence of operations in a mathematical expression. The absence of parentheses in "x 3 8 x 2" forces us to rely on this principle, highlighting its importance in ensuring consistent results.
-
Commutative Property of Multiplication: This property states that the order of factors in a multiplication operation doesn't affect the product (a * b = b * a). In our analysis, we saw how different groupings, though seemingly altering the order, yielded the same result (48x) due to the commutative property.
-
Associative Property of Multiplication: This property states that the grouping of factors in multiplication doesn't affect the product ((a * b) * c = a * (b * c)). While not explicitly demonstrated in the initial simplification, the consistent result highlights an underlying application of this property.
Frequently Asked Questions (FAQ)
-
Q: What is the single correct answer to "x 3 8 x 2"?
-
A: There isn't a single correct answer without further clarification. The expression's ambiguity allows for multiple interpretations, all leading to variations of 48x. The "correct" answer depends entirely on the intended order of operations, which should be explicitly defined using parentheses or other grouping symbols.
-
Q: Why is it important to use parentheses in mathematical expressions?
-
A: Parentheses eliminate ambiguity and ensure clear communication of the intended order of operations. They prevent misinterpretations and errors, especially in more complex equations.
-
Q: Can this expression be solved without knowing the value of 'x'?
-
A: No, without additional information or an equation, we can only simplify the expression to a multiple of 'x' (48x). We cannot determine a numerical value for 'x' from the expression alone.
-
Q: What mathematical concepts does this problem illustrate?
-
A: The problem illustrates the importance of order of operations, the commutative and associative properties of multiplication, and the need for clear mathematical notation to avoid ambiguity.
Conclusion: The Value of Ambiguity in Learning Mathematics
While initially presented as a simple puzzle, "x 3 8 x 2" offers a valuable lesson in the precision required in mathematical notation and the importance of understanding the fundamental principles governing mathematical operations. The ambiguity inherent in the expression highlights the potential for misinterpretations and emphasizes the crucial role of clarity in expressing mathematical ideas. By exploring the multiple interpretations and solutions, we've gained a deeper appreciation for the nuances of algebraic manipulation and the power of well-defined mathematical language. It serves as a reminder that even seemingly simple problems can reveal profound insights into the underlying structure of mathematics. The lack of definitive solution, in turn, stimulates further exploration and critical thinking, enhancing the learning process.
Latest Posts
Latest Posts
-
Khan Academy Black Hole Badge
Sep 22, 2025
-
Cell And Cell Division Notes
Sep 22, 2025
-
Types Of Questions For Comprehension
Sep 22, 2025
-
Anatomy And Physiology Blood Quiz
Sep 22, 2025
-
Acceleration Graph Vs Velocity Graph
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X 3 8 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.