X 3 X 1 Simplify
zacarellano
Sep 21, 2025 · 5 min read
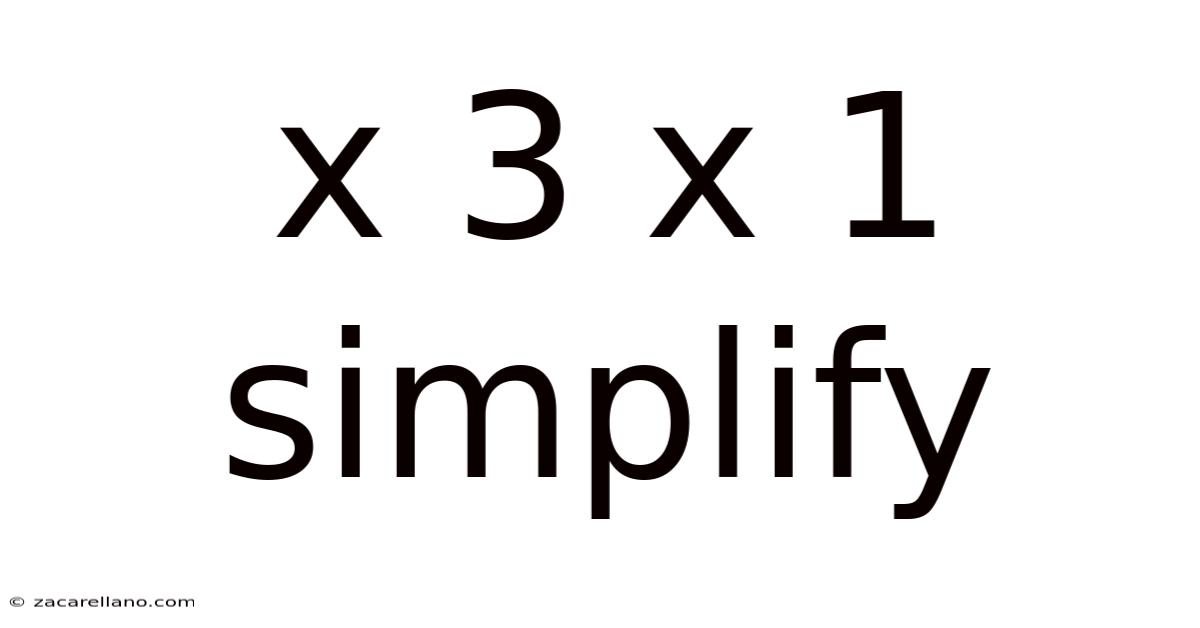
Table of Contents
Simplifying x³ x 1: A Deep Dive into Algebraic Expressions
Understanding how to simplify algebraic expressions is a fundamental skill in mathematics. This article will provide a comprehensive guide to simplifying the expression x³ x 1, explaining the underlying principles and expanding on related concepts. We'll cover the basics of exponents, the multiplicative identity property, and how these concepts work together to arrive at the simplest form of this expression. This guide is designed for students of all levels, from those just beginning their algebra journey to those seeking a more robust understanding of algebraic simplification.
Introduction: Understanding the Basics
Before diving into the simplification of x³ x 1, let's review some essential mathematical concepts. This section serves as a foundation for understanding the steps involved in simplifying the expression.
1. Variables and Exponents: In algebra, we use variables, often represented by letters like x, y, or z, to represent unknown or unspecified numbers. Exponents, written as superscripts, indicate repeated multiplication. For example, x³ means x * x * x (x multiplied by itself three times).
2. The Multiplicative Identity Property: This crucial property states that any number multiplied by 1 remains unchanged. Formally, for any number 'a', a x 1 = a. This property is the cornerstone of simplifying our expression.
3. Order of Operations (PEMDAS/BODMAS): Remember the order of operations, often represented by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). This ensures consistent results when evaluating expressions. In our case, we'll focus on multiplication.
Step-by-Step Simplification of x³ x 1
Now, let's simplify the expression x³ x 1 step-by-step:
-
Identify the components: We have two components: x³ and 1. x³ represents x multiplied by itself three times, and 1 is the multiplicative identity.
-
Apply the multiplicative identity property: According to the multiplicative identity property, any number multiplied by 1 remains unchanged. Therefore, x³ x 1 = x³.
-
Final Simplified Form: The simplest form of the expression x³ x 1 is x³. This is because multiplying x³ by 1 does not alter its value.
Deeper Dive: Exploring Related Concepts
While the simplification of x³ x 1 is straightforward, understanding the broader mathematical context enriches our understanding. Let's explore some related concepts:
1. Multiplication of Monomials: A monomial is a single term algebraic expression. Our expression involves the multiplication of two monomials: x³ and 1. The general rule for multiplying monomials is to multiply the coefficients (numbers in front of the variables) and then multiply the variables, adding their exponents if the base is the same.
For example: 2x² * 3x⁴ = (2 * 3) * (x² * x⁴) = 6x⁶. In our case, the coefficient of x³ is 1 (implicitly), and the coefficient of 1 is, well, 1. So, 1 * 1 = 1 and x³ remains x³.
2. Exponents and their Properties: Understanding exponent properties is vital for simplifying more complex algebraic expressions. Key properties include:
* **Product of Powers:** xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾ (When multiplying terms with the same base, add the exponents). This is especially relevant when dealing with expressions like x² * x⁵ = x⁷.
* **Power of a Power:** (xᵃ)ᵇ = x⁽ᵃ*ᵇ⁾ (When raising a power to another power, multiply the exponents). For example, (x²)³ = x⁶.
* **Quotient of Powers:** xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾ (When dividing terms with the same base, subtract the exponents).
* **Zero Exponent:** x⁰ = 1 (Any non-zero number raised to the power of zero equals 1).
* **Negative Exponents:** x⁻ⁿ = 1/xⁿ (A negative exponent indicates the reciprocal of the base raised to the positive exponent).
3. Polynomial Operations: Understanding how to simplify x³ x 1 is a building block for working with polynomials (expressions consisting of multiple terms). Polynomials can involve addition, subtraction, and multiplication of monomials.
Frequently Asked Questions (FAQ)
Q1: What if the expression was x³ x 2 instead of x³ x 1?
A1: If the expression was x³ x 2, the simplified form would be 2x³. The coefficient 2 would simply multiply the term x³.
Q2: Can we simplify x³ x 0?
A2: Yes, anything multiplied by zero is zero. Therefore, x³ x 0 = 0.
Q3: How does this relate to more complex algebraic expressions?
A3: Simplifying x³ x 1 demonstrates the fundamental principle of the multiplicative identity. This principle applies broadly to more complex algebraic manipulations, including factoring, expanding, and solving equations. Mastering this basic simplification is crucial for tackling more advanced problems.
Q4: What if there were more variables involved, such as x³y² x 1?
A4: The multiplicative identity property still applies. x³y² x 1 simplifies to x³y². The '1' doesn't change the other variables.
Conclusion: The Importance of Foundational Concepts
Simplifying the expression x³ x 1, while seemingly basic, highlights the importance of understanding fundamental algebraic concepts such as exponents and the multiplicative identity property. These concepts are essential building blocks for more complex algebraic manipulations. By mastering these basic principles, you lay a solid foundation for success in higher-level mathematics. Remember, practice is key; the more you work with these concepts, the more intuitive they will become. Continue exploring different algebraic expressions, applying the rules and properties discussed above, and you'll find your ability to simplify and solve problems greatly increases. The journey to algebraic proficiency starts with these seemingly simple yet powerful steps.
Latest Posts
Latest Posts
-
How To Find Power Series
Sep 21, 2025
-
3 Digit Addition Word Problems
Sep 21, 2025
-
Single Replacement And Double Replacement
Sep 21, 2025
-
1 1 2 Yards To Inches
Sep 21, 2025
-
Photosynthesis Occurs In Which Organelle
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 1 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.