X 4 X 4 Simplify
zacarellano
Sep 09, 2025 · 5 min read
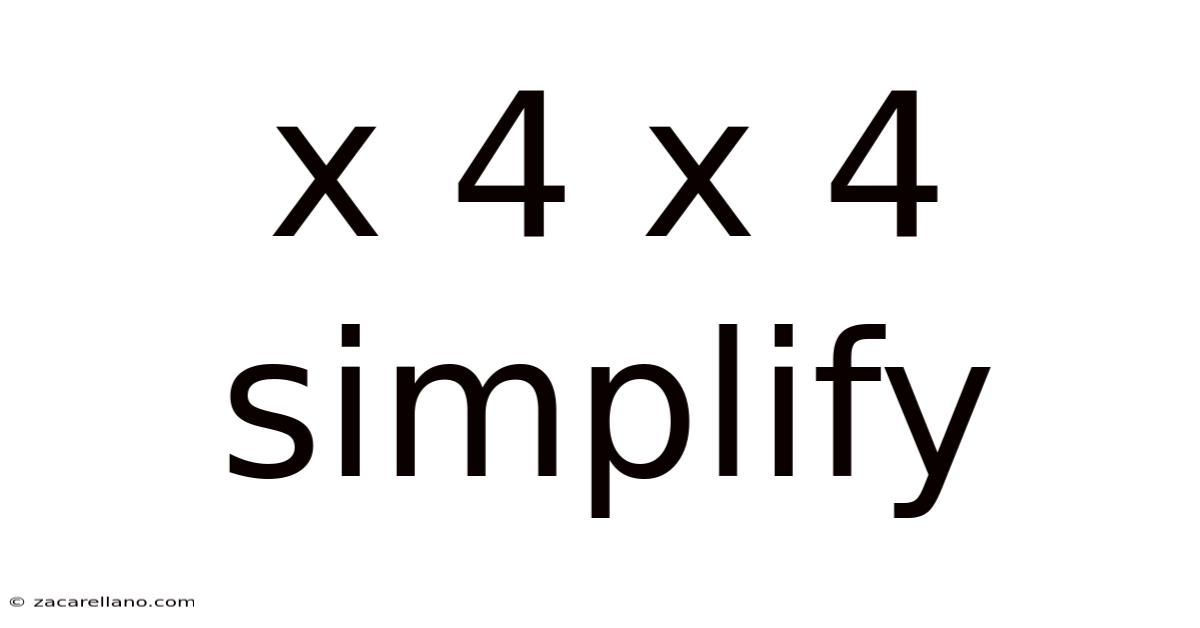
Table of Contents
Simplifying x⁴/x⁴: A Deep Dive into Algebraic Simplification
Understanding how to simplify algebraic expressions is fundamental to success in mathematics. This article provides a comprehensive guide to simplifying the expression x⁴/x⁴, exploring not only the straightforward solution but also the underlying mathematical principles and potential extensions. We will cover various approaches, address common misconceptions, and delve into the broader context of algebraic simplification, equipping you with the tools to confidently tackle similar problems.
Introduction: Understanding the Problem
The expression x⁴/x⁴ represents a fraction where both the numerator (top) and the denominator (bottom) are the same: x raised to the power of 4. Simplifying this expression involves finding its simplest equivalent form. This seemingly simple problem offers an excellent opportunity to explore fundamental concepts in algebra, including exponents, division rules, and the concept of undefined expressions. The keyword here is simplification, which means reducing the expression to its most concise and easily understandable form.
Method 1: Using the Quotient Rule of Exponents
The most straightforward approach involves applying the quotient rule of exponents. This rule states that when dividing exponential expressions with the same base, you subtract the exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>. In our case, a = x, m = 4, and n = 4.
Applying the rule:
x⁴ / x⁴ = x<sup>(4-4)</sup> = x⁰
Now, any non-zero number raised to the power of zero equals 1. Therefore:
x⁰ = 1 (provided x ≠ 0)
This is our simplified expression. The caveat, "provided x ≠ 0," is crucial. Division by zero is undefined in mathematics; therefore, the simplification to 1 is only valid when x is not equal to zero.
Method 2: Expanding the Expression
Alternatively, we can simplify by expanding the expression. x⁴ means x multiplied by itself four times (x * x * x * x). Therefore, x⁴/x⁴ can be written as:
(x * x * x * x) / (x * x * x * x)
Notice that each 'x' in the numerator can be cancelled out by a corresponding 'x' in the denominator. This leaves us with:
1/1 = 1
Again, this simplification is valid only if x ≠ 0. If x were 0, we would have 0/0, which is an indeterminate form, not a defined value.
Method 3: Considering the Concept of Division
Let's approach the problem from a purely divisional perspective. Division essentially asks: "How many times does the denominator go into the numerator?" In this case, we're asking: "How many times does x⁴ go into x⁴?" The answer is clearly one time. This reinforces the simplification to 1, again with the crucial condition that x ≠ 0.
The Importance of the Condition x ≠ 0
The repeated emphasis on the condition x ≠ 0 is paramount. This highlights a crucial aspect of algebraic manipulation: always be mindful of the domain of the variables involved. Failing to consider this can lead to incorrect conclusions and mathematical errors. The expression x⁴/x⁴ simplifies to 1 only when x is any real number except zero.
Extending the Concept: Simplifying Similar Expressions
Understanding the simplification of x⁴/x⁴ provides a solid foundation for tackling more complex expressions. Let's examine some variations:
-
x<sup>m</sup>/x<sup>m</sup>: Following the same logic, this expression simplifies to 1, provided x ≠ 0. The exponent 'm' could be any integer.
-
x<sup>5</sup>/x<sup>2</sup>: Applying the quotient rule, we get x<sup>(5-2)</sup> = x³.
-
(2x²)<sup>3</sup> / (x³)³: This involves expanding the powers first. The numerator becomes 8x⁶, and the denominator becomes x⁹. Applying the quotient rule, we get 8x<sup>(6-9)</sup> = 8x<sup>-3</sup> = 8/x³.
-
(x² + 2x + 1) / (x + 1): This requires factoring the numerator. The numerator is a perfect square trinomial, factoring to (x + 1)(x + 1). Therefore, the expression simplifies to (x + 1), provided x ≠ -1 (to avoid division by zero).
Common Mistakes to Avoid
-
Forgetting the condition x ≠ 0: This is the most common error. Always remember that division by zero is undefined.
-
Incorrect application of exponent rules: Carefully review and understand the rules of exponents before attempting simplifications.
-
Not factoring completely: When dealing with polynomial expressions, ensure that you factor them completely before canceling terms.
Frequently Asked Questions (FAQ)
-
Q: What happens if x = 0?
- A: If x = 0, the expression becomes 0/0, which is an indeterminate form. It doesn't have a defined value.
-
Q: Can I simplify x⁴/x⁴ to 0?
- A: No. Only if x=0, and even then, it's indeterminate. For all other x-values, it simplifies to 1.
-
Q: Are there any other ways to simplify x⁴/x⁴ besides the ones mentioned?
- A: While the methods described are the most common and efficient, one could theoretically expand the expression fully and then cancel terms manually. However, this is less efficient for higher exponents.
-
Q: How does this relate to calculus?
- A: Understanding simplification is critical in calculus, particularly when dealing with limits and derivatives. Simplifying expressions often makes them easier to manipulate and analyze.
Conclusion: Mastering Algebraic Simplification
Simplifying the expression x⁴/x⁴, seemingly simple at first glance, offers a valuable opportunity to reinforce our understanding of fundamental algebraic concepts. By mastering these principles, including the quotient rule of exponents, the importance of considering the domain of variables, and the avoidance of common errors, we build a strong foundation for tackling more complex algebraic problems. Remember the key takeaway: x⁴/x⁴ simplifies to 1, provided x ≠ 0. This understanding forms a cornerstone of further mathematical exploration. Always strive for accuracy and clarity in your simplifications, ensuring you consider all possible conditions and apply the rules correctly. Through practice and attention to detail, you will steadily improve your skills in algebraic simplification.
Latest Posts
Latest Posts
-
What Is A Parallel Side
Sep 09, 2025
-
Ap Environmental Science Unit 7
Sep 09, 2025
-
Math Word Problems 3rd Grade
Sep 09, 2025
-
How To Study For Dsat
Sep 09, 2025
-
Area Model For Multiplying Fractions
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about X 4 X 4 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.