X Divided By X Squared
zacarellano
Sep 10, 2025 · 4 min read
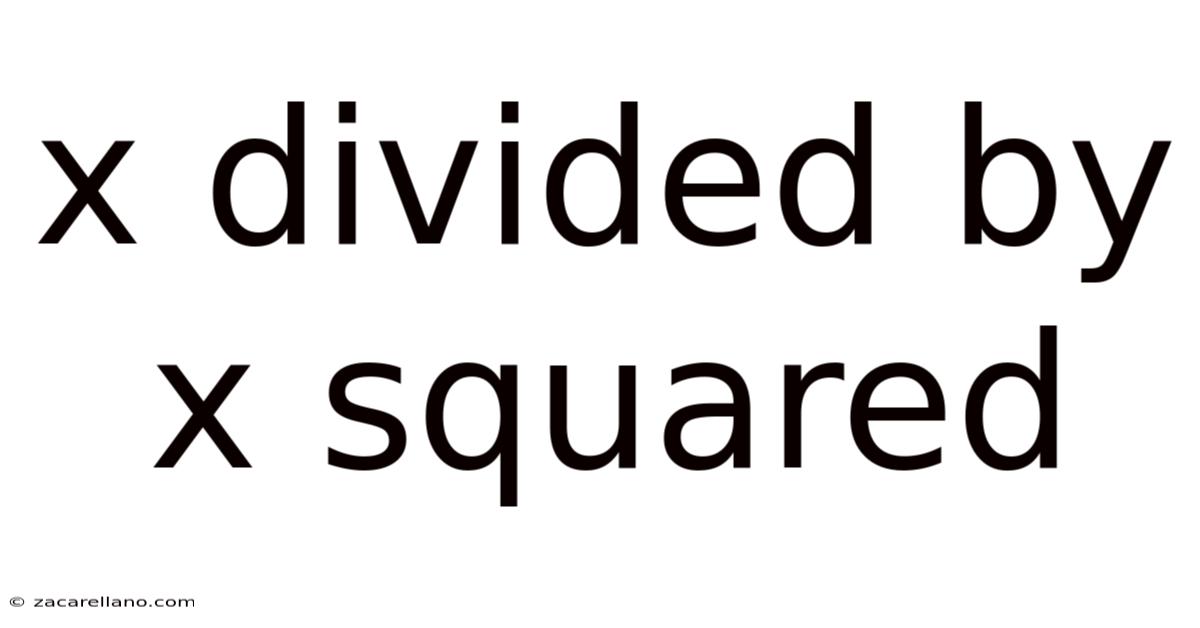
Table of Contents
Understanding x Divided by x Squared: A Deep Dive into Algebraic Simplification
Dividing x by x squared, or x/x², is a fundamental concept in algebra that often trips up students. This seemingly simple problem unveils deeper principles of algebraic manipulation and simplification, which are crucial for more advanced mathematical concepts. This comprehensive guide will walk you through the process, explaining the rules involved, providing step-by-step examples, and addressing common misconceptions. We'll delve into the underlying mathematical principles and explore how this concept applies to various areas of mathematics and beyond.
Understanding the Basics: Exponents and Division
Before tackling x/x², let's refresh our understanding of exponents and their role in division. An exponent (or power) indicates how many times a base number is multiplied by itself. For instance, x² means x * x.
When we divide terms with the same base (in this case, 'x'), we subtract the exponents. This is a key rule governing algebraic simplification. Consider the example: x⁵ / x². Following the rule, we subtract the exponent in the denominator (2) from the exponent in the numerator (5): 5 - 2 = 3. Therefore, x⁵ / x² simplifies to x³.
Step-by-Step Simplification of x/x²
Now, let's apply this rule to our problem: x/x².
-
Identify the base and exponents: The base is 'x'. The numerator has an exponent of 1 (since x¹ = x), and the denominator has an exponent of 2.
-
Apply the rule of exponent subtraction: Subtract the exponent of the denominator from the exponent of the numerator: 1 - 2 = -1.
-
Write the simplified expression: This results in x⁻¹.
-
Understanding Negative Exponents: A negative exponent indicates the reciprocal. Therefore, x⁻¹ is equivalent to 1/x.
Therefore, the simplified form of x/x² is 1/x.
Visualizing the Simplification: A Fractional Approach
We can also approach this problem from a fractional perspective. Remember that x² means x * x. So, x/x² can be written as:
x / (x * x)
Now, we can cancel out one 'x' from the numerator and denominator:
(x / x) * (1 / x) = 1 / x
This method visually demonstrates the simplification process and reinforces the concept of canceling common factors.
Expanding the Concept: Different Scenarios with x, y, and Constants
Let's explore some variations to deepen our understanding:
-
Scenario 1: (3x³) / (x²): Here, we have a coefficient (3) and higher exponents. We simplify as follows:
- Divide the coefficients: 3 / 1 = 3
- Subtract the exponents: 3 - 2 = 1
- Result: 3x¹ or simply 3x
-
Scenario 2: (5x²y³) / (xy²): This example includes two variables. We handle each variable separately:
- Coefficients: 5 / 1 = 5
- Variable x: 2 - 1 = 1
- Variable y: 3 - 2 = 1
- Result: 5xy
-
Scenario 3: (10x⁴y²) / (5x³y⁵): This involves both coefficients and negative exponents after simplification:
- Coefficients: 10 / 5 = 2
- Variable x: 4 - 3 = 1
- Variable y: 2 - 5 = -3
- Result: 2x¹y⁻³ which simplifies to 2x/y³
The Importance of Understanding Zero and Undefined Values
It's crucial to acknowledge the limitations. While x/x² simplifies to 1/x, we must consider the case where x = 0.
- When x = 0: The original expression, x/x², becomes 0/0, which is undefined. Division by zero is not permitted in mathematics. The simplified expression, 1/x, is also undefined when x = 0.
Therefore, while the simplification is valid for all x ≠ 0, we must always state this condition to avoid mathematical errors.
Applications in Calculus and Beyond
Understanding the simplification of expressions like x/x² is fundamental to more advanced mathematical concepts. It's crucial in:
-
Calculus: Derivatives and integrals frequently involve simplifying rational expressions, including those with similar bases and exponents.
-
Physics and Engineering: Many physical laws and engineering equations involve algebraic manipulations, where simplifying expressions like x/x² is essential for problem-solving.
-
Computer Science: In algorithm analysis and computational complexity, simplifying expressions helps determine the efficiency of algorithms.
Frequently Asked Questions (FAQ)
Q1: Can I multiply the exponents when dividing x by x²?
No, you subtract the exponents when dividing terms with the same base. Multiplying exponents is applicable when raising a power to another power (e.g., (x²)³ = x⁶).
Q2: What if the exponent in the denominator is larger than the exponent in the numerator?
As we saw in the example x/x², you will end up with a negative exponent in the simplified expression, which represents the reciprocal.
Q3: Why is division by zero undefined?
Division is the inverse of multiplication. If a/b = c, then b * c = a. There is no number 'c' that satisfies 0 * c = a (for any a ≠ 0). Therefore, division by zero is undefined.
Conclusion: Mastering Algebraic Simplification
Mastering the simplification of expressions like x/x² is a cornerstone of algebraic proficiency. It's not just about getting the correct answer; it's about understanding the underlying principles of exponents, division, and the limitations of mathematical operations like division by zero. Through consistent practice and a clear understanding of these principles, you'll be well-equipped to tackle more complex algebraic problems and advance your mathematical journey. Remember to always double-check your work and consider the domain restrictions of your simplified expressions, especially when dealing with variables that could potentially be zero. The ability to simplify algebraic expressions effectively will serve you well throughout your academic and professional pursuits.
Latest Posts
Latest Posts
-
Imperial Bureaucracy Ap World Hiistory
Sep 10, 2025
-
Derivative Of A Vector Function
Sep 10, 2025
-
Growth Mindset Activities For Students
Sep 10, 2025
-
Difference Between Conductor And Insulator
Sep 10, 2025
-
Algebra X On Both Sides
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about X Divided By X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.