X + Xy + Y
zacarellano
Sep 13, 2025 · 5 min read
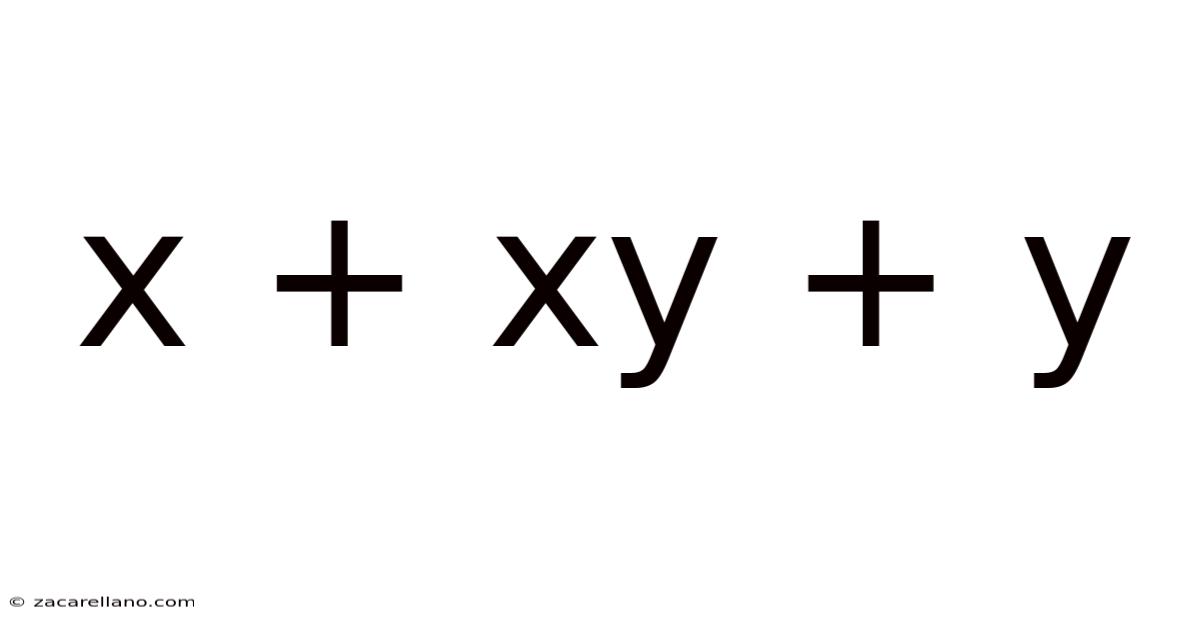
Table of Contents
Exploring the Algebraic Expression: x + xy + y
This article delves into the algebraic expression x + xy + y, exploring its properties, potential simplifications, and applications. We'll cover various approaches to understanding this seemingly simple expression, revealing its hidden complexities and demonstrating its relevance in various mathematical contexts. Understanding this expression provides a strong foundation for tackling more advanced algebraic manipulations and problem-solving.
Introduction
The expression x + xy + y, although concise, presents opportunities for insightful mathematical exploration. At first glance, it may seem uncomplicated, but a deeper analysis reveals several interpretations and potential manipulations depending on the context and available information. We'll examine methods for simplification, factoring, and interpreting the expression's behavior under different conditions. This understanding is crucial in fields like algebra, calculus, and even computer programming where such expressions form the building blocks of more complex equations and algorithms.
Understanding the Components
Before we delve into the manipulations, let's understand the individual components:
- x: This represents a variable, a symbol that can take on different numerical values.
- y: Another variable, independent of x, also capable of representing different numerical values.
- xy: This represents the product of x and y. It's important to note the implicit multiplication; there's no explicit multiplication symbol between x and y.
The expression x + xy + y is a polynomial, specifically a trinomial (a polynomial with three terms) consisting of two variables. The degree of the polynomial is 2, determined by the highest power of the variables (xy has a combined power of 2: x¹y¹).
Methods for Simplification and Factoring
Unfortunately, there's no straightforward simplification of x + xy + y into a more compact form without additional information or constraints. However, we can explore different factoring techniques to potentially reveal underlying relationships.
1. Common Factor Extraction (Partial Factoring):
We can partially factor the expression by observing that 'y' is a common factor in two of the three terms:
x + y(1 + x)
This factorization isolates the 'y' variable, separating it from the 'x' term. While not a complete factorization, it can be useful in certain contexts, such as solving equations where y is a known value.
2. Factoring Based on Specific Conditions:
If we have additional information about the relationship between x and y, further factorization might be possible. For instance:
- If x = 1: The expression simplifies to 1 + 1*y + y = 1 + 2y. This is a linear expression in 'y'.
- If y = 1: The expression simplifies to x + x*1 + 1 = 2x + 1. Again, a linear expression, this time in 'x'.
- If x = -1: The expression simplifies to -1 + (-1)y + y = -1, a constant value. This highlights the importance of the values of the variables.
These examples demonstrate how the value and relationships between x and y significantly impact the expression's simplification.
3. Considering the Expression as a Function:
We can consider x + xy + y as a function of two variables: f(x, y) = x + xy + y. Analyzing this function's behavior can be insightful. We could:
- Find partial derivatives: This allows us to examine the rate of change of the function with respect to x or y independently.
- Plot the function: A three-dimensional plot would visualize the function's surface, revealing its characteristics. This would require software capable of plotting 3D functions.
Solving Equations Involving x + xy + y
The expression often appears within more complex equations. Let's explore a scenario:
Suppose we have the equation: x + xy + y = 10
Solving this equation for x or y requires additional information or manipulation. We can attempt to solve for one variable in terms of the other. For example, let's solve for y:
x + xy + y = 10 y(1 + x) = 10 - x y = (10 - x) / (1 + x)
This expresses y as a function of x. Similarly, we could solve for x in terms of y. However, without further constraints or information, we cannot find unique numerical solutions for both x and y.
Applications of x + xy + y
Although seemingly simple, this expression finds applications in various areas:
- Modeling Systems: In systems modeling, such expressions can represent relationships between variables. For example, in economics, x and y could represent quantities of two goods, and the expression could represent a combined cost or utility function.
- Linear Algebra: The expression could be embedded within larger matrix equations or systems of linear equations.
- Computer Programming: Such expressions are common building blocks in programming algorithms and calculations.
Frequently Asked Questions (FAQ)
-
Q: Can x + xy + y always be simplified? A: No, without additional information or constraints on x and y, there is no simpler equivalent form. The partial factoring mentioned earlier is the most significant simplification achievable generally.
-
Q: What are the practical uses of this expression? A: It can be used in modeling systems, solving equations, and forming parts of more complex mathematical constructs, especially in the field of algebra and linear algebra.
-
Q: Can we use graphical methods to understand this expression? A: Yes. We can plot the function f(x, y) = x + xy + y as a 3D surface. This visual representation aids in understanding the expression's behavior for various values of x and y.
-
Q: How does the expression behave when x and y are large numbers? A: As x and y grow larger, the xy term will dominate the expression, making its overall value increase rapidly. The impact of 'x' and 'y' individually becomes less significant compared to their product.
-
Q: What if x or y is equal to zero? A: If x = 0, the expression simplifies to y. If y = 0, the expression simplifies to x. If both x and y are 0, the expression evaluates to 0.
Conclusion
The seemingly simple algebraic expression x + xy + y, though not directly simplifiable in its general form, provides fertile ground for exploration and understanding. Through partial factoring, examining its behavior under various conditions, and considering its representation as a function of two variables, we can extract valuable insights. Its applications extend beyond its immediate simplicity, making it a fundamental concept in algebra and related fields. Understanding this expression builds a solid foundation for more complex algebraic manipulation and problem-solving in various mathematical and applied contexts. It underscores the importance of examining even seemingly straightforward mathematical expressions for hidden complexities and potential applications. The more deeply we explore even seemingly simple problems, the more we discover about the elegance and power of mathematics.
Latest Posts
Latest Posts
-
First Vs Second Great Awakening
Sep 14, 2025
-
Math Notes For 5th Graders
Sep 14, 2025
-
Ap Physics 1 Unit 3
Sep 14, 2025
-
Types Of Collisions In Physics
Sep 14, 2025
-
Scatter Plot Questions And Answers
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X + Xy + Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.