Y Absolute Value Of X
zacarellano
Sep 19, 2025 · 6 min read
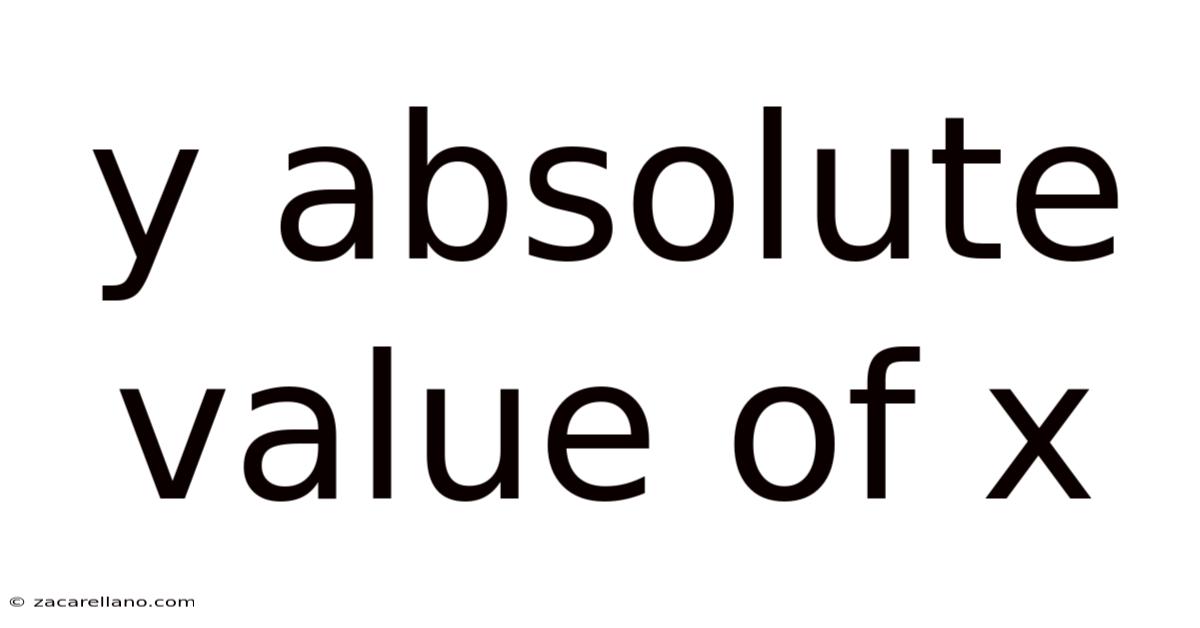
Table of Contents
Understanding the Absolute Value of x: A Comprehensive Guide
The absolute value of x, denoted as |x|, is a fundamental concept in mathematics with far-reaching applications across various fields. This comprehensive guide will delve into the definition, properties, graphical representation, and practical applications of the absolute value, ensuring a thorough understanding for learners of all levels. We'll explore its use in solving equations and inequalities, and clarify common misconceptions.
What is the Absolute Value?
The absolute value of a number is its distance from zero on the number line. Regardless of whether the number is positive or negative, the absolute value is always non-negative. Formally, we define the absolute value of x as follows:
|x| = x, if x ≥ 0 |x| = -x, if x < 0
This definition might seem slightly confusing at first. Let's break it down:
- If x is zero or positive: The absolute value of x is simply x itself. For example, |5| = 5 and |0| = 0.
- If x is negative: The absolute value of x is the opposite (or negation) of x. For example, |-5| = -(-5) = 5. This ensures that the distance is always positive.
In essence, the absolute value function "strips away" the negative sign if present, leaving only the magnitude of the number.
Graphical Representation of the Absolute Value Function
The graph of y = |x| is a V-shaped curve. The vertex of the V is at the origin (0,0). For x ≥ 0, the graph coincides with the line y = x. For x < 0, the graph coincides with the line y = -x. This creates the characteristic V-shape. Understanding this visual representation is crucial for grasping the behavior of the absolute value function.
This V-shape helps visualize the concept of distance. The y-coordinate represents the distance of x from zero.
Properties of the Absolute Value
The absolute value function possesses several important properties that are frequently used in mathematical manipulations:
- Non-negativity: |x| ≥ 0 for all x.
- Symmetry: |-x| = |x| for all x.
- Product rule: |xy| = |x| |y| for all x and y.
- Quotient rule: |x/y| = |x|/|y| for all x and y, provided y ≠ 0.
- Triangle inequality: |x + y| ≤ |x| + |y| for all x and y. This is a powerful inequality with many applications in analysis.
- Absolute value of a difference: |x - y| represents the distance between x and y on the number line.
These properties are not just theoretical; they are essential tools for simplifying expressions, solving equations, and proving mathematical theorems.
Solving Equations Involving Absolute Value
Solving equations containing absolute values requires careful consideration of the definition. We must consider two cases:
Case 1: The expression inside the absolute value is non-negative. In this case, we can simply remove the absolute value signs.
Case 2: The expression inside the absolute value is negative. In this case, we remove the absolute value signs and negate the expression.
Let's illustrate with an example:
Solve |x - 2| = 5
Case 1: x - 2 ≥ 0
x - 2 = 5 x = 7
Case 2: x - 2 < 0
-(x - 2) = 5 -x + 2 = 5 -x = 3 x = -3
Therefore, the solutions are x = 7 and x = -3.
More complex equations may require a combination of algebraic manipulations and case-by-case analysis. Always check your solutions by substituting them back into the original equation.
Solving Inequalities Involving Absolute Value
Inequalities involving absolute values also require a case-by-case analysis, but the approach differs slightly. Here are some common scenarios:
- |x| < a: This inequality is equivalent to -a < x < a. The solution is an interval.
- |x| > a: This inequality is equivalent to x < -a or x > a. The solution consists of two disjoint intervals.
- |x - c| < a: This represents the values of x that are within a distance 'a' from 'c'. It is equivalent to c - a < x < c + a.
- |x - c| > a: This represents the values of x that are farther than a distance 'a' from 'c'. It's equivalent to x < c - a or x > c + a.
Remember to always check your solutions by substituting values from the solution set into the original inequality.
Applications of Absolute Value
The absolute value function finds applications in numerous fields, including:
- Physics: Calculating distances, speeds, and accelerations. For example, speed is often represented as the absolute value of velocity to indicate magnitude regardless of direction.
- Engineering: Error analysis and tolerance calculations. Absolute values help quantify the deviation from expected values.
- Computer science: Determining the magnitude of differences between values, particularly in algorithms and data structures.
- Statistics: Calculating deviations from the mean, measuring error, and analyzing data variability. Absolute deviation is a common measure of data spread.
- Finance: Determining the magnitude of profits and losses, irrespective of whether they are gains or losses.
- Calculus: Defining limits, continuity, and derivatives. The absolute value function plays a key role in the study of piecewise functions and limits.
Common Misconceptions about Absolute Value
It is crucial to address some common misconceptions to prevent errors:
- Misunderstanding the definition: Students often forget that |x| = -x only when x is negative.
- Incorrectly applying properties: Misapplying the properties of absolute values can lead to incorrect solutions.
- Ignoring case analysis when solving equations and inequalities: Failing to consider both positive and negative cases when solving equations or inequalities involving absolute value is a common mistake.
- Confusing absolute value with negation: The absolute value is not simply removing the negative sign; it's about representing the distance from zero.
Frequently Asked Questions (FAQ)
Q: Can the absolute value of a number ever be negative?
A: No. By definition, the absolute value is always non-negative (zero or positive).
Q: What is the difference between |x| and -|x|?
A: |x| represents the distance from zero. -|x| represents the negative of that distance. For example, if x = 5, |x| = 5 and -|x| = -5.
Q: How do I solve an equation like |x| = |y|?
A: This equation implies that x and y are equidistant from zero. Therefore, x = y or x = -y.
Q: Can I distribute an absolute value over addition or subtraction?
A: No, the absolute value does not distribute over addition or subtraction. |x + y| ≠ |x| + |y| in general. The triangle inequality provides a relationship, but it's an inequality, not an equality.
Q: What is the derivative of |x|?
A: The derivative of |x| is 1 for x > 0, -1 for x < 0, and undefined at x = 0. This reflects the piecewise nature of the absolute value function.
Conclusion
The absolute value of x, although seemingly simple at first glance, is a powerful concept with diverse applications in mathematics and beyond. A solid understanding of its definition, properties, and methods for solving equations and inequalities involving absolute values is essential for success in various mathematical and scientific pursuits. By carefully applying the principles outlined in this guide and avoiding common misconceptions, you can confidently tackle problems involving the absolute value function. Remember to always check your solutions and practice regularly to build a firm grasp of this fundamental concept. The more you work with absolute values, the more intuitive and comfortable you will become with this essential mathematical tool.
Latest Posts
Latest Posts
-
Sin Pi 4 Unit Circle
Sep 19, 2025
-
8th Grade Science Standards California
Sep 19, 2025
-
Why Is Text Structure Important
Sep 19, 2025
-
Diff Between Ligaments And Tendons
Sep 19, 2025
-
Gcf For 12 And 36
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Y Absolute Value Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.