5 6 X 1 2
zacarellano
Sep 18, 2025 · 5 min read
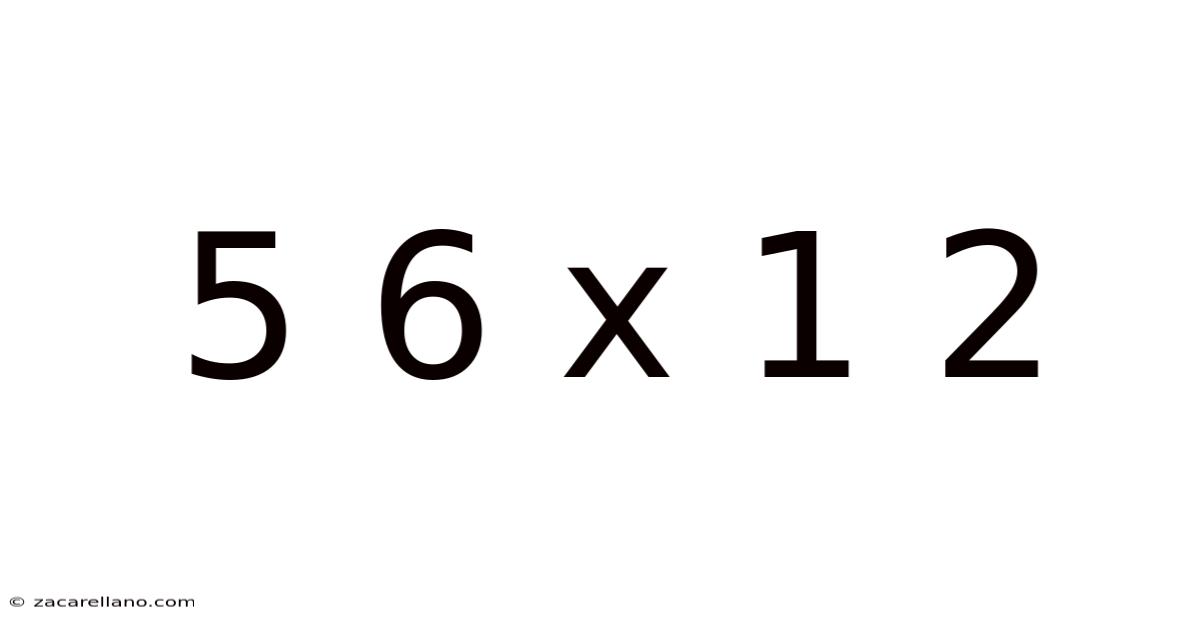
Table of Contents
Decoding 5/6 x 1/2: A Deep Dive into Fraction Multiplication
This article provides a comprehensive guide to understanding and solving fraction multiplication problems, specifically focusing on the example 5/6 x 1/2. We will explore the underlying principles, various methods for solving the problem, and delve into the practical applications of fraction multiplication in everyday life. Whether you're a student struggling with fractions or an adult looking to refresh your math skills, this detailed explanation will equip you with the knowledge and confidence to tackle similar problems.
Introduction: Understanding Fractions and Multiplication
Fractions represent parts of a whole. The top number is called the numerator, indicating how many parts we have, and the bottom number is the denominator, indicating the total number of equal parts the whole is divided into. Multiplying fractions involves finding a fraction of a fraction, which might initially seem complex, but with the right approach, it becomes straightforward. Our focus problem, 5/6 x 1/2, asks us to find one-half of five-sixths.
Method 1: The Straightforward Approach – Multiply Numerators and Denominators
The simplest method for multiplying fractions is to multiply the numerators together and the denominators together separately. Let's apply this to our problem:
5/6 x 1/2 = (5 x 1) / (6 x 2) = 5/12
This directly gives us the answer: 5/12. This method is efficient and works well for all fraction multiplication problems.
Method 2: Visual Representation – Using Area Models
Visual aids can be incredibly helpful in understanding fraction multiplication, especially for beginners. Imagine a rectangle representing the whole. Divide it into six equal columns (representing the denominator of 5/6). Shade five of these columns to represent 5/6.
Now, divide the entire rectangle into two equal rows (representing the denominator of 1/2). You'll notice that the rectangle is now divided into 12 equal parts (6 columns x 2 rows = 12). The area that is both shaded (representing 5/6) and in the top row (representing 1/2) is 5 out of the 12 equal parts. This visually confirms that 5/6 x 1/2 = 5/12.
Method 3: Simplifying Before Multiplication – Canceling Common Factors
Sometimes, we can simplify the calculation before multiplying by canceling out common factors between the numerators and denominators. While not necessary in this particular problem (as there are no common factors), let’s explore this method using a different example:
(2/3) x (3/4)
Here, we can see that the numerator 2 and the denominator 4 share a common factor of 2 (2/4 simplifies to 1/2). Similarly, the numerator 3 and denominator 3 share a common factor of 3. We can cancel these out:
(2/3) x (3/4) = (2 x 3) / (3 x 4) = (2/4) x (3/3) = (1/2) x (1/1) = 1/2
This method streamlines the multiplication and often results in a simpler fraction that needs less reduction.
Explanation of the Calculation: 5/6 x 1/2 = 5/12
Multiplying fractions essentially means finding a fraction of another fraction. In this case, we're finding one-half (1/2) of five-sixths (5/6). The result, 5/12, means that if we divide a whole into 12 equal parts, five of those parts represent one-half of five-sixths of the whole.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just a theoretical exercise; it's used extensively in various real-world situations:
- Cooking and Baking: Adjusting recipes often involves fraction multiplication. For instance, if a recipe calls for 2/3 cup of flour and you want to halve the recipe, you'd multiply 2/3 by 1/2.
- Construction and Measurement: Calculating material quantities, determining precise measurements, and scaling blueprints frequently involve fractions and their multiplication.
- Finance and Budgeting: Calculating percentages, determining discounts, and managing portions of a budget all rely on the principles of fraction multiplication.
- Data Analysis: In statistics and data analysis, representing proportions and understanding relationships between datasets often involves using fractions and multiplication.
Frequently Asked Questions (FAQs)
Q1: Why do we multiply the numerators and denominators separately?
This stems from the distributive property of multiplication. When we multiply fractions, we are effectively multiplying the numerators and denominators separately to represent the combined parts of the whole.
Q2: What if one of the fractions is a whole number?
A whole number can be expressed as a fraction with a denominator of 1. For example, 3 can be written as 3/1. Then, apply the usual multiplication method: (3/1) x (1/2) = (3 x 1) / (1 x 2) = 3/2 or 1 1/2.
Q3: How do I simplify a fraction after multiplication?
To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by that number. For example, to simplify 6/12, the GCD is 6. Dividing both the numerator and denominator by 6 gives 1/2.
Q4: What if I get a result that's an improper fraction (numerator larger than denominator)?
An improper fraction can be converted into a mixed number. For example, 7/4 can be converted to 1 3/4 by dividing the numerator by the denominator (7 ÷ 4 = 1 with a remainder of 3). The quotient (1) becomes the whole number part, and the remainder (3) becomes the numerator of the fraction, with the denominator remaining the same (4).
Q5: Are there any online tools or calculators for multiplying fractions?
Yes, many online calculators can perform fraction multiplication. However, it's crucial to understand the underlying process to truly grasp the concept and apply it effectively in various contexts.
Conclusion: Mastering Fraction Multiplication
Understanding and mastering fraction multiplication is a fundamental skill in mathematics with far-reaching applications. While initially seeming daunting, the process is quite straightforward once the underlying principles are grasped. Whether you use the direct multiplication method, a visual representation, or simplification before multiplication, the key is to systematically multiply the numerators and the denominators. Through practice and understanding, you will build confidence and proficiency in tackling fraction multiplication problems of varying complexity. Remember, practice makes perfect! So, grab a pen and paper, try some more fraction multiplication problems, and enjoy the process of expanding your mathematical abilities.
Latest Posts
Latest Posts
-
Limiting Reagent Problems With Answers
Sep 18, 2025
-
Negative 4 Minus Negative 7
Sep 18, 2025
-
Unit 8 Ap Calc Ab
Sep 18, 2025
-
New England Colonies Social Structure
Sep 18, 2025
-
Is Electric Field A Vector
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 6 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.