Negative 4 Minus Negative 7
zacarellano
Sep 18, 2025 · 5 min read
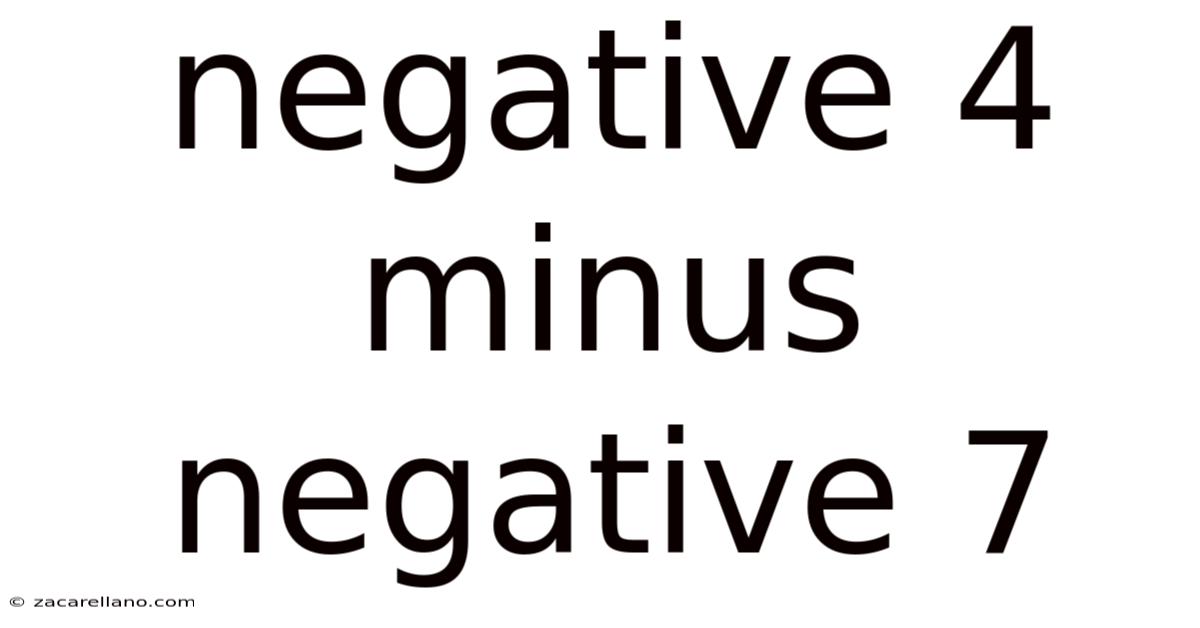
Table of Contents
Decoding the Mystery: Negative 4 Minus Negative 7
Understanding integer arithmetic, particularly involving negative numbers, can be a stumbling block for many. This comprehensive guide will unravel the seemingly complex problem of "negative 4 minus negative 7," providing a step-by-step explanation, exploring the underlying mathematical principles, and addressing frequently asked questions. By the end, you'll not only know the answer but also grasp the fundamental concepts that govern operations with negative numbers. This will build a strong foundation for tackling more advanced mathematical concepts.
Understanding Negative Numbers
Before diving into the problem, let's solidify our understanding of negative numbers. Negative numbers represent values less than zero. They are often used to represent quantities like debt, temperature below freezing, or positions below sea level. On a number line, negative numbers are located to the left of zero. The further left a number is on the number line, the smaller its value.
Think of a number line as a visual representation of numbers. Zero sits in the middle, positive numbers extend to the right, and negative numbers extend to the left. This visual tool is incredibly helpful for understanding addition and subtraction with negative numbers.
The Problem: -4 - (-7)
Our core problem is: -4 - (-7). This might look daunting at first, but we can break it down into manageable steps. The key is understanding the concept of subtracting a negative number.
Step-by-Step Solution
-
Understanding Subtraction as Adding the Opposite: Subtraction is essentially the inverse operation of addition. Subtracting a number is equivalent to adding its opposite. The opposite of a number is its additive inverse; it's the number that, when added to the original number, results in zero. For example, the opposite of 5 is -5, and the opposite of -3 is 3.
-
Rewriting the Equation: Applying this rule to our problem, we can rewrite "-4 - (-7)" as "-4 + (+7)". Notice that subtracting a negative number (-7) becomes adding its opposite (+7).
-
Performing the Addition: Now we have a simpler addition problem: -4 + 7. We can visualize this on a number line. Start at -4. Adding 7 means moving seven units to the right on the number line.
-
The Result: After moving seven units to the right from -4, we land on 3. Therefore, -4 - (-7) = 3.
Visual Representation on a Number Line
Imagine a number line. Start at -4. To subtract -7, we add its opposite, which is +7. This means we move 7 units to the right. This journey takes us from -4 to 3.
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
^ ^
|-4- |3 - Result
| +7 |
The Mathematical Explanation: Additive Inverse and Properties of Integers
The solution relies on fundamental properties of integers:
- Additive Inverse: Every integer has an additive inverse. The additive inverse of 'a' is '-a', because a + (-a) = 0.
- Associative Property of Addition: The way we group numbers in addition doesn't change the sum. For example, (a + b) + c = a + (b + c).
- Commutative Property of Addition: The order in which we add numbers doesn't change the sum. For example, a + b = b + a.
By applying the additive inverse, we transform the subtraction problem into an addition problem, making it easier to solve using the number line or other methods.
Extending the Concept: More Complex Problems
The principles discussed here apply to more complex problems involving multiple negative numbers and subtractions. For instance:
-
-5 - (-2) - (-8): First, rewrite this as -5 + 2 + 8. Then, solve the addition: -5 + 2 = -3, and -3 + 8 = 5. The answer is 5.
-
-10 - (-3) + (-6): Rewrite as -10 + 3 - 6. Solve step-by-step: -10 + 3 = -7, and -7 - 6 = -13. The answer is -13.
Remember the key steps:
- Change subtraction of a negative to addition of a positive.
- Simplify the expression by combining like terms.
- Use a number line or other visual aids if needed.
Frequently Asked Questions (FAQ)
Q1: Why does subtracting a negative number result in addition?
A1: Subtraction is the opposite of addition. Subtracting a negative number is like "undoing" the subtraction of a positive number. It's like adding the positive version back into the equation.
Q2: Can I solve this problem using a calculator?
A2: Yes, most calculators will correctly handle this type of calculation. However, understanding the underlying principles is crucial for solving more complex problems and developing a solid mathematical foundation.
Q3: What if I have a problem with more than two negative numbers?
A3: Apply the same principle: change each subtraction of a negative number to an addition of a positive number. Then, simplify and solve using the order of operations (PEMDAS/BODMAS).
Q4: Are there other ways to visualize this problem besides a number line?
A4: Yes, you could use colored counters (red for negative, black for positive) or even a simple drawing to represent the numbers and their addition/subtraction.
Conclusion: Mastering Negative Numbers
Understanding integer operations, especially those involving negative numbers, is a cornerstone of mathematical proficiency. The seemingly complicated problem of "-4 - (-7)" becomes straightforward when we grasp the concept of adding the opposite and apply the fundamental properties of integers. By breaking down the problem into smaller steps and using visual aids like the number line, we can easily arrive at the correct answer (3) and develop a deeper understanding of negative number arithmetic. This knowledge will serve as a solid foundation for more complex mathematical concepts in the future, empowering you to approach challenges with confidence and a clear understanding of the underlying principles. Remember, practice is key! The more you work with negative numbers, the more intuitive these operations will become.
Latest Posts
Latest Posts
-
Art Of The Counter Reformation
Sep 19, 2025
-
Central Limit Theorem Ap Stats
Sep 19, 2025
-
8 25 As A Decimal
Sep 19, 2025
-
What Is A Latin Forum
Sep 19, 2025
-
Radius Of A Cone Calculator
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Negative 4 Minus Negative 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.